Mesh Analysis -konseptit, menetelmät, esimerkit

Hän Mesh -analyysi Se on tekniikka, jota käytetään tasaisten sähköpiirien ratkaisemiseen. Tämä menettely voi esiintyä myös kirjallisuudessa menetelmänimillä piirivirrat o Menetelmä Verkkovirrat (tai silmukka).

Tämän ja muiden sähköpiirin analyysimenetelmien perusta on Kirchhoffin ja Ohmin lain lakeja. Kirchhoffin laki puolestaan ​​ovat eristettyjen järjestelmien fysiikan säilyttämisperiaatteen ilmaisuja: Sekä sähköinen varaus että energia säilytetään.

Kuvio 1. Piirit ovat osa lukemattomia laitteita. Lähde: Pixabay.

Toisaalta sähkövaraus liittyy virtaan, joka on liikkuva kuormitus, kun taas piirissä energia on kytketty jännitteeseen, joka on agentti, joka vastaa tarvittavan työn tekemisestä liikkeen pitämiseksi.

Nämä tasaiseen piiriin sovelletut lait luovat joukon samanaikaisia ​​yhtälöitä, jotka on ratkaistava virran tai jännitearvojen saamiseksi.

Yhtälöjärjestelmä voidaan ratkaista jo tunnetuilla analyyttisillä tekniikoilla, kuten Cramer -sääntö, joka vaatii determinanttien laskelman järjestelmäliuoksen saamiseksi.

Yhtälöiden lukumäärästä riippuen ne ratkaistaan ​​tieteellisellä laskimella tai matemaattisella ohjelmistolla. Verkossa on myös monia vaihtoehtoja.

[TOC]

Tärkeät ehdot

Ennen kuin selitämme miten se toimii, aloitamme määrittelemällä nämä termit:

Haara: Osa, joka sisältää piirin elementin.

Solmu: kohta, joka yhdistää kaksi tai useampia oksia.

Nauha: Se on mikä tahansa piirin suljettu osa, joka alkaa ja päättyy samaan solmuun.

Keikari: silmukka, joka ei sisällä muuta sidosta sisällä (välttämätön mesh-A.

Menetelmät

Mesheal -analyysi on yleinen menetelmä, jonka tarkoituksena on ratkaista piirejä, joiden elementit on kytketty sarjaan, rinnakkain tai sekoitettuna, ts. Kun yhteystyyppiä ei ole selvästi erotettu. Piirin on oltava tasainen tai ainakin on oltava mahdollista maksaa se sellaisenaan.

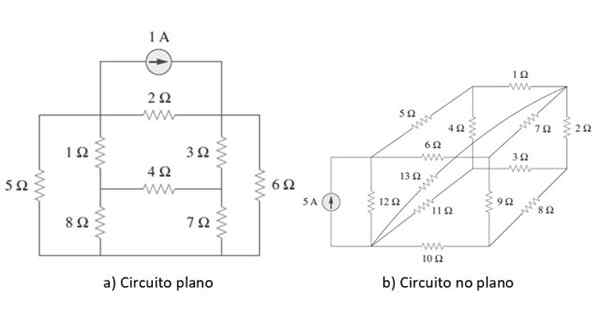Kuva 2. Litteät ja ei -flat -piirit. Lähde: Alexander, c. 2006. Sähköpiirin säätiöt. Kolmas. Painos. MC Graw Hill.

Esimerkki jokaisesta piirin tyypistä on esitetty yllä olevassa kuvassa. Kun piste on selkeytetty, aloittata, käytämme menetelmää yksinkertaiseen piiriin esimerkkinä seuraavassa osassa, mutta ennen kuin tarkistamme lyhyesti Ohmin ja Kirchhoffin lakeja.

Ohmin laki: Sean V Jännite, R - vastus e Yllyttää Ohmisten resistiivisen elementin virta, jossa jännite ja virta ovat suoraan verrannollisia, vastus on suhteellisuuden vakio:

Voi palvella sinua: API Gravity: Scale and luokittelu raakaöljyn

V = i.R -

Jännite Kirchhoff Law (LKV): Missä tahansa yhdellä suuntaan kulkevalla suljetussa etenemissuunnassa jännitteiden algebrallinen summa on nolla. Tämä sisältää lähteistä, vastuksista, induktoreista tai kondensaattorista johtuvat jännitteet: ∑ E = ∑ r_Yllyttää. Yllyttää

Virran Kirchhoff (LKC): Missä tahansa solmussa virtojen algebrallinen summa on nolla, ottaen huomioon. Tällä tavalla: ∑ i = 0.

Mesh -virtausmenetelmällä se ei ole välttämätöntä.

- Vaiheet mesh -analyysin soveltamiseksi

Alamme selittää 2 meshes -piirin menetelmän. Menettelyä voidaan laajentaa myöhemmin suuremmille piireille.

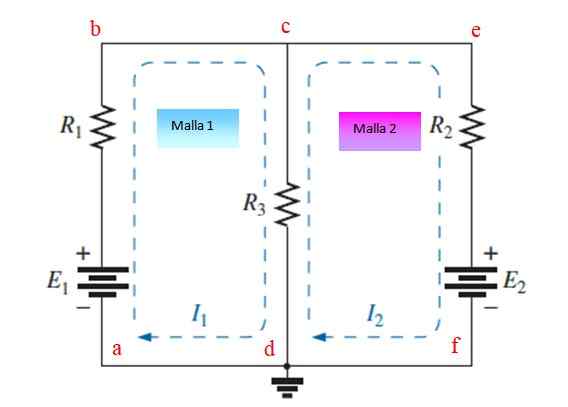Kuva 3. Piiri, jossa vastus ja lähteet on järjestetty kahteen silmään. Lähde: f. Zapata.

Vaihe 1

Määritä ja piirrä riippumattomat virrat jokaiselle verkkoon, tässä esimerkissä ne ovat Yllyttää₁ ja Yllyttää₂. Ne voidaan piirtää aikataulussa tai myös anti -Horary.

Vaihe 2

Käytä Kirchhoffin jännitteiden lakia (LTK) ja Ohmin lakia jokaiselle verkkoon. Potentiaalisille putouksille annetaan merkki (-), kun taas korotuksille osoitetaan merkki (+).

Abcda -verkko

Alkaen pisteestä A ja virran merkityksen seurauksena löydämme potentiaalin nousun akku E1 (+), sitten R -lasku₁ (-) ja sitten toinen lasku r₃ (-).

Samanaikaisesti vastus r₃ Sen ylittää myös virta i₂, Mutta vastakkaiseen suuntaan, siksi se edustaa nousua (+). Ensimmäinen yhtälö on näin:

JA₁-R -₁.Yllyttää₁ -R -₃.Yllyttää₁ + R -₃.Yllyttää₂ = 0

Välittömästi factoring ja uudelleenlähettävät ehdot:

- (R₁+R -₃) Yo₁ +R -₃Yllyttää₂ = -E₁  (Yhtälö 1)

CEFDC -verkko 

Alkaen pisteestä ja ja virran merkityksen seuraaminen on potentiaalinen lasku R -₂ (-), toinen lasku JA₂, Koska virta tulee akun navan + läpi ja lopulta uusi pudotus R -₃ (-), samanaikaisesti virta Yllyttää₁ Se ylittää R -₃ Vastakkaiseen suuntaan (+).

Toinen yhtälö osoitetut merkit jäävät tällä tavalla:

- R -₂ Yllyttää₂ - JA₂ -R -₃ Yllyttää₂ +R -₃ Yllyttää₁= 0

R -₃Yllyttää₁ - (R₂ +R -₃₎ Yllyttää₂ = E₂  (Yhtälö 2)

Huomaa, että on olemassa kaksi yhtälöä kahdella tuntemattomalla ja₁ ja minä₂.

Vaihe 3

Silloin muodostettu yhtälöjärjestelmä on ratkaistu.

Ratkaisut

Aluksi on tärkeää ottaa huomioon seuraava:

-Solmiot tai verkkovirrat voidaan antaa mielivaltaiseen suuntaan.

-Jokaiselle välttämättömälle verkolle - tai “ikkunaan” - että piirille on osoitettava virta.

Voi palvella sinua: isocoric -prosessi

-Mesh -virtauksia kutsutaan isoilla kirjaimilla, jotta ne voidaan erottaa sivukonttoreissa kiertävistä virroista, vaikka joissain tapauksissa haaran läpi kiertävä virta voi sama kuin verkko.

- Esimerkki 1

Löydä virrat, jotka kiertävät jokaisen vastustuksen läpi kuvan 3 piirissä, jos elementeillä on seuraavat arvot:

R -₁ = 20 Ω; R -₂ = 30 Ω; R -₃ = 10 Ω; JA₁ = 12 V; JA₂ = 18 V

Ratkaisu

Ensinnäkin on tarpeen määrittää verkkovirrat ja₁ ja minä₂ ja ota yhtälöjärjestelmä, joka on päätetty edellisessä osassa, korvaa sitten lauseessa annetut arvot:

- (R₁+R -₃) Yo₁ +R -₃Yllyttää₂ = -E₁  (Yhtälö 1)

R -₃Yllyttää₁ - (R₂ +R -₃₎ Yllyttää₂ = E₂     (Yhtälö 2)

-

-(20+30) Yllyttää₁ + 10i₂ = -12

10i₁ - (30 +10) i₂ = 18      

--

-viisikymmentäYllyttää₁ + 10i₂ = -12

10i₁ - 40 i₂ = 18      

Koska se on 2 x 2 yhtälöjärjestelmä, se voidaan helposti ratkaista pelkistämällä, kertomalla 5: llä toisella yhtälöllä tuntemattoman eliminoimiseksi Yllyttää₁-

-viisikymmentäYllyttää₁ + 10 i₂ = -12

50i₁ - 200 i₂ = 90

-     

-190 i₂= 78

Yllyttää₂ = - 78/180 a = - 0.41 a

Virta tyhjennetään heti Yllyttää₁ mistä tahansa alkuperäisestä yhtälöstä:

Yllyttää₁ = (18 + 40 I₂) / 10 = (18 + 40 x (-0.41)) / 10 = 0.16 a

Negatiivinen merkki nykyisessä Yllyttää₂ tarkoittaa, että 2 meshin virta kiertää piirustuksen vastaisesti.

Kunkin vastusvirrat ovat seuraavat:

Vastustuskykyä R -₁ Virta kiertää Yllyttää₁ = 0.16 a siinä mielessä, vastustuskyky R -₂ Virta kiertää Yllyttää₂ = 0.41 a Vastoin vedettyjä ja vastustuskykyä R -₃ kiertää Yllyttää₃ = 0.16- (-0.41) a = 0.57 a alas.

Järjestelmäratkaisu Cramerin menetelmällä

Matriisilla järjestelmä voidaan ratkaista seuraavasti:

Vaihe 1: Laske δ

 Tärkeä: Kun Δ = 0, järjestelmässä ei ole ratkaisua, se on yhteensopimaton järjestelmä.

Vaihe 2: Laske δ₁

Ensimmäinen sarake korvataan yhtälöjärjestelmän riippumattomilla ehdoilla ylläpitämällä järjestelmää, jolla järjestelmä alun perin nostettiin:

Vaihe 3: Laske I₁

Yllyttää₁ = Δ₁/Δ = 300/1900 = 0.16 a

Vaihe 4: Laske δ₂

 Vaihe 5: Laske I₂

Yllyttää₂ = Δ₂/Δ = -780/1900 = -0.41 a

- Esimerkki 2

Määritä virta ja jännitteet jokaisen vastus seuraavan piirin avulla verkkovirtausmenetelmällä:

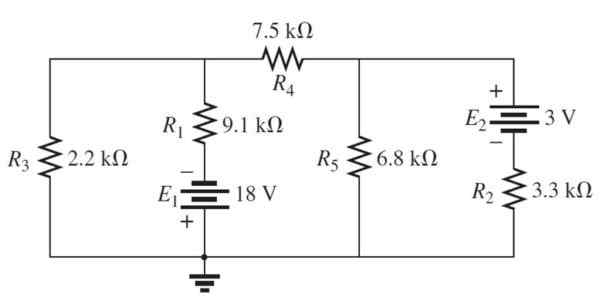Kuva 4. 3 verkkopiiri. Lähde: Boylestad, R. 2011. Johdanto piirianalyysiin.Toinen. Painos. Pearson.

Ratkaisu

Kolme mesh -virtaa vedetään, kuten seuraavassa kuvassa esitetään, mielivaltaisissa aisteissa. Nyt silmät juoksevat mistä tahansa:

Se voi palvella sinua: IMANTANTION: Mikä koostuu, menetelmä ja esimerkit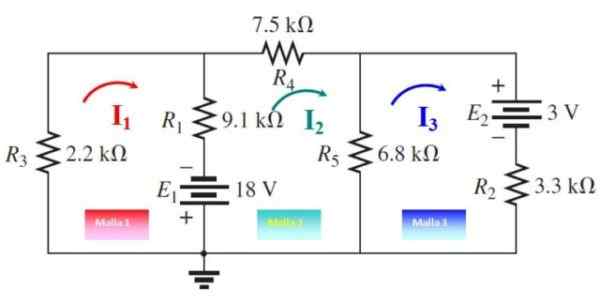 Kuva 5. Verkkovirrat harjoitukselle 2. Lähde: f. Zapata, muokattu boylestadista.

Mesh 1

-9100.Yllyttää₁+18-2200.Yllyttää₁+9100.Yllyttää₂= 0

-11300 I₁ + 9100.Yllyttää₂ = -18

Mesh 2       

-(7500 +6800 +9100) .Yllyttää₂ + 9100.Yllyttää₁+6800.Yllyttää₃-18 = 0

9100.Yllyttää₁ - 23400.Yllyttää₂ + 6800.Yllyttää₃ = 18

Mesh 3  

-(6800 + 3300) i₃ + 6800.Yllyttää₂ - 3 = 0

6800.Yllyttää₂ - 10100.Yllyttää₃ = 3

Yhtälöjärjestelmä

-11300 I₁ + 9100.Yllyttää₂ + 0 -.Yllyttää₃= -18

9100.Yllyttää₁ - 23400.Yllyttää₂ + 6800.Yllyttää₃ = 18

0 -.Yllyttää₁ + 6800.Yllyttää₂ - 10100.Yllyttää₃ = 3

Vaikka numerot ovat suuret, se ratkaistaan ​​nopeasti tieteellisen laskimen avulla. Muista, että yhtälöt on tilataan ja lisätä nollia paikkoihin, joissa tuntematon.

Verkkovirrat ovat:

Yllyttää₁ = 0.0012 a; Yllyttää₂ = -0.00048 A; Yllyttää₃ = -0.00062 a

Virrat Yllyttää₂ ja Yllyttää₃ Ne kiertävät kuvassa vastakkaiseen suuntaan, koska ne osoittautuivat negatiivisiksi.

Jokaisessa vastusvirta- ja jännitteitä koskeva taulukko

Vastus (ω)	Virta (ampeerit)	Jännite = i.R (voltit)
9100	Yllyttää1 -Yllyttää2 = 0.0012-(-0.00048) = 0.00168	viisitoista.3
3300	0 -.00062	2.05
2200	0 -.0012	2.64
7500	0 -.00048	3.60 60
6800	Yllyttää2 -Yllyttää3= -0.00048-(-0.00062) = 0.00014	0 -.95

Cramer -sääntöratkaisu

Koska ne ovat suuria määriä, on kätevää käyttää tieteellistä merkintää työskennelläkseen suoraan heidän kanssaan.

I: n laskenta₁

3 x 3: n determinantin väri -nuolet osoittavat, kuinka numeeriset arvot löydetään, kertomalla ilmoitetut arvot. Aloitetaan hankkimalla Determinant δ: n ensimmäisen kiinnikkeen henkilöt:

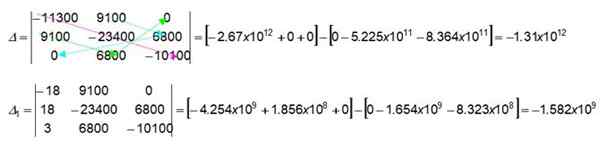
(-11300) x (-23400) x (-10100) = -2.67 x 10¹²

9100 x 0 x 0 = 0 -

9100 x 6800 x 0 = 0 -

Saamme heti toisen kiinnikkeen samaan determinanttiin, joka toimii vasemmalta oikealle (tälle kiinnikkeelle värillisiä nuolia ei piirretty kuvaan). Kutsumme lukijan tarkistamaan sen:

0 x (-23400) x 0 = 0

9100 x 9100 x (-10100) = -8.364 x 10^yksitoista

6800 x 6800 x (-11300) = -5.225 x 10^yksitoista

Samoin lukija voi myös tarkistaa determinantin arvot Δ₁.

Tärkeä: Molempien kiinnikkeiden välillä on aina negatiivinen merkki.

Lopuksi virta saadaan Yllyttää₁ kautta Yllyttää₁ = Δ₁ / Δ

Yllyttää₁ = -1.582 x 10⁹/-1.31 x 10¹² = 0.0012 a                                   

I: n laskenta₂

Menettely voidaan toistaa laskemiseksi Yllyttää₂, Tässä tapauksessa determinantin δ laskeminen₂ A δ -determinantin toinen sarake korvataan riippumattomien termien sarakkeella ja sen arvo löytyy, selitetyn menettelyn mukaisesti.

Kuten on hankalaa suurten määrien takia, etenkin jos tieteellistä laskinta ei ole, yksinkertaisin on korvata arvo Yllyttää₁ jo laskettuna seuraavassa yhtälössä ja selkeä:

-11300 I₁ + 9100.Yllyttää₂ + 0 -.Yllyttää₃= -18 → 9100 I₂= -18 + 11300 I₁ → I₂ = -0.00048 a

I3 -laskenta

Kerran Yllyttää₁ ja Yllyttää₂ Kädessä, Yllyttää₃ Se löytyy suoraan korvaamisella.

Viitteet

1. Alexander, c. 2006. Sähköpiirin säätiöt. Kolmas. Painos. MC Graw Hill.
2. Boylestad, r. 2011. Johdanto piirianalyysiin.Toinen. Painos. Pearson.
3. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Nide 5. Sähköinen vuorovaikutus. Toimittanut Douglas Figueroa (USB).
4. Garcia, L. 2014. Sähkömagnetismi. Toinen. Painos. Santanderin teollisuusyliopisto.
5. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Nide 2.