Tekijäraunan määritelmä, kaavat ja harjoitukset

Hän Tekijärapu Se on yksinkertainen kone, joka koostuu hihnapyörän järjestelystä, jolla on kertoimen voimanvaikutus. Tällä tavoin voit nostaa kuorman, joka käyttää vain murto -osan painosta köyden vapaassa päässä.

Se koostuu kahdesta sarjasta hihnapyörät: toinen, joka on kiinnitetty tukeen ja toinen, joka käyttää tuloksena olevaa voimaa kuormitukseen. Hihnapyörät on asennettu yleensä metalliselle kehykselle, joka pitää niitä. 

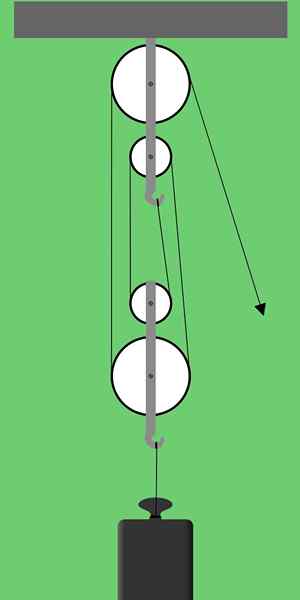
Kuvio 1. Tekijäraunan kaavio. Lähde: Pixabay

Kuvio 1 esittää tekijäraunaa, joka koostuu kahdesta kahden hihnapyörän ryhmästä. Tämän tyyppisiä hihnapyöräjärjestelyjä kutsutaan myös Sarja jompikumpi Polypassit.

[TOC]

Tekijäretkiset kaavat

Tapaus 1: matkapuhelin ja kiinteä

Ymmärtääksemme, miksi tämä järjestely kertoo kohdistetun voiman, aloitamme yksinkertaisimmalla tapauksella, joka koostuu kiinteästä ja liikkuvasta hihnapyörästä.

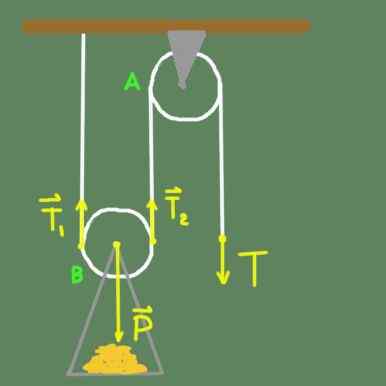Kuva 2. Kaksi hihnapyörää.

Kuvassa 2 meillä on kiinteä hihnapyörä katolle tuella. Hihnapyörä A. Meillä on myös B -hihnapyörä, jolla on kiinteä tuki hihnapyörän akselille, johon kuorma asetetaan. Hihnapyörä B on mahdollisuus liikkua pystysuunnassa sen lisäksi, että se pystyy kiertämään vapaasti akselinsa ympärillä.

Oletetaan, että olemme tasapainotilanteessa. Harkitse B -hihnapyörällä toimivia voimia. B -Pulley -akseli tukee kokonaispainoa P, joka on suunnattu alaspäin. Jos tämä olisi silloin ainoa voima B -hihnapyörään, mutta tiedämme, että tämän hihnapyörän läpi kulkeva köyttä on myös kaksi voimaa, jotka ovat T1 ja T2, jotka on suunnattu ylöspäin.

Translaatiotasapainon varalta kahden voiman on oltava samat painoon, joka tukee hihnapyörää B -akselia.

T1 + t2 = p

Mutta koska hihnapyörä B on myös pyörimis tasapainossa, niin T1 = T2. T1- ja T2 -voimat tulevat köyteen kohdistuvasta jännityksestä, nimeltään T.

Se voi palvella sinua: Bohr Atomic -malli

Siksi t1 = t2 = t. Edellisen yhtälön korvaaminen on edelleen:

T + t = p

2T = P

Osoittaa, että köyteen kohdistuva jännitys on vain puolet painosta:

T = p/2

Esimerkiksi, jos kuorma olisi 100 kg, se riittää levittämään 50 kg: n voima köyden vapaaseen päähän kuorman nostamiseksi vakiona nopeudella.

Tapaus 2: Kaksi matkapuhelinta ja kaksi kiinteää hihnapyörää

Tarkastellaan jännitteitä ja voimia, jotka toimivat sarjassa, joka koostuu kahdesta tuesta A ja B kahdella hihnapyörällä.

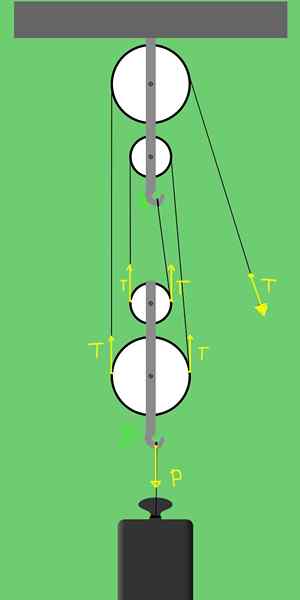Kuva 3. Voimat 2 kiinteän hihnapyörän ja 2 liikkuvan hihnapyörän takilla.

Tuki B: llä on mahdollisuus liikkua pystysuunnassa ja pojan kanssa toimivat voimat:

- Kuorman paino P, joka osoittaa pystysuunnassa.

- Kaksi jännitettä suuressa hihnapyörässä ja kaksi jännitteet pienessä hihnapyörässä. Kaiken kaikkiaan neljä jänniä, kaikki osoittavat.

Jotta translaatiotasapaino olisi, on välttämätöntä, että voimat, jotka pisteitä pystysuoraan ylöspäin ovat yhtä suuret kuin alaspäin osoittavat kuorma. Eli se on täytettävä:

T + t + t + t = p

Eli 4 t = p

Mistä seuraa, että köyden vapaassa päässä oleva käytetty voima t on vain neljäsosa painosta johtuen kuormasta, joka haluaa nousta., T = p / 4.

Tällä T -jännitteen arvolla kuorma voidaan pitää staattisena tai kasvaa vakiona nopeudella. Jos käytetään suurempaa jännitettä kuin tämä arvo, kuorma kiihtyy, ehto, joka on välttämätön sen poistamiseksi muusta.

Yleinen tapaus: n matkapuhelimet ja n kiinteät hihnapyörät

Kuten edellisissä tapauksissa nähdään, matkapuhelinten jokaisella hihnapyörällä on pari voimaa ylöspäin köyden kautta, joka kulkee hihnapyörän läpi. Mutta tämä voima ei voi olla mitään muuta kuin köyteen kohdistuva jännitys vapaassa päässä.

Joten jokaiselle matkapuhelimen hihnapyörällä on ylöspäin suuntautuva voima, joka on 2T: n arvoinen. Mutta koska matkapuhelinjoukossa on n hihnapyöriä, on sitten tarpeen osoittaa pystysuoraan ylöspäin: on:

Voi palvella sinua: Squirrel Cage Engine

2 n t

Pystysuoran tasapainon kannalta on välttämätöntä, että:

2 n t = p

Siksi vapaaseen päähän kohdistuva voima on:

T = p / (2 n)

Tässä tapauksessa voidaan sanoa, että voima T: lle kerrotaan 2 n kertaa kuormalla.

Esimerkiksi, jos meillä olisi 3 kiinteän hihnapyörän ja 3 matkapuhelimen tekijäraukku, luku n olisi yhtä suuri kuin 3. Toisaalta, jos kuorma olisi p = 120 kg, niin vapaaseen päähän kohdistettu voima olisi t = 120 kg / (2*3) = 20 kg.

Ratkaisut

Harjoitus 1

Harkitse tekijälaitetta, joka koostuu kahdesta kiinteästä hihnapyörästä ja kahdesta matkapuhelimesta. Suurin jännitys, joka voi tukea köyttä on 60 kg. Määritä, mikä on maksimikuorma, joka voidaan sijoittaa.

Ratkaisu

Kun kuorma on levossa tai liikkuu jatkuvasti painoa P -arvo, se liittyy köydessä levitettävään jännitykseen seuraavan suhteen avulla:

P = 2 n t

Koska se on kahden liikkuva ja kahden kiinteän hihnapyörän takila, sitten n = 2.

Suurin kuorma, joka voidaan sijoittaa.

Suurin kuorma = 2*2*60 kg = 240 kg

Harjoitus 2

Löydä köyden jännitteen ja kuorman painon välinen suhde kahden hihnapyörän tekijärapuun, jossa kuorma kiihtyy kiihtymällä.

Ratkaisu

Ero tässä esimerkissä suhteessa tähän mennessä nähtyyn on, että järjestelmän dynamiikkaa on harkittava. Joten ehdotamme Newtonin toista lakia pyydetyn suhteen löytämiseksi.

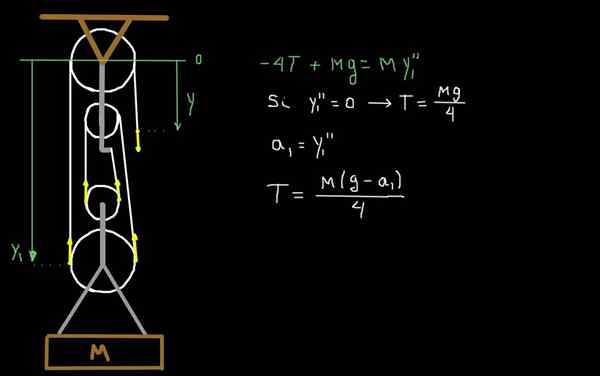Kuva 4. Tekijäraunan dynamiikka.

Kuviossa 4 piirrämme voimat köyden jännityksen t. Laitteen mobiiliosalla on kokonaismassa m. Otamme vertailujärjestelmänä yhden ensimmäisen kiinteän ja positiivisen hihnapyörän tasolla.

Y1 on alin hihnapyörän akselin sijainti.

Käytämme Newtonin toista lakia määrittääksemme takilan mobiiliosan A1 -kiihtyvyyden:

Voi palvella sinua: Varignon -lause

-4 t + mg = m A1

Koska kuorman paino on p = mg, missä g on painovoiman kiihtyvyys, edellinen suhde voidaan kirjoittaa:

-4T + p = p (a1 / g)

Jos halusimme määrittää köydessä kohdistetun jännityksen, kun tietty painolaino on kiihdytetty kiihtyvyydellä A1, niin edellinen suhde olisi tällainen:

T = p (1 - a1 / g) / 4

Huomaa, että jos järjestelmä oli levossa tai liikkuessa jatkuvasti, niin A1 = 0, ja palautimme saman lausekkeen, jonka saimme tapauksessa 2.

Harjoitus 3

Tässä esimerkissä käytetään samaa harjoituksen 1 laitetta, samalla köydellä, joka tukee korkeintaan 60 kg jännitystä. Tietty kuorma nousee, kiihdyttäen sitä leposta 1 m/s 0,5 s: llä, käyttämällä köyden maksimaalista jännitystä. Löydä enimmäiskuorman paino.

Ratkaisu

Käytämme harjoituksessa 2 saatuja lausekkeita ja kuviossa 4 olevaa vertailujärjestelmää, jossa positiivinen osoite on pystysuora alaspäin.

Kuorman kiihtyvyys on a1 = (-1 m/s -0 m/s) /0,5 s = -2 m/s^2.

Kuorman paino kilogrammissa on annettu

P = 4 T / (1 - A1 / G)

P = 4*60 kg / (1 + 2/9.8) = 199,3 kg

Tämä on kuorman suurin mahdollinen paino ilman, että köyttä rikkoutuu. Huomaa, että saatu arvo on pienempi kuin esimerkissä 1 saatu.

Viitteet

1. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1. 101-120.
2. Resnick, r. (1999). Fyysinen. Osa. 1. 3 ra ed. espanjaksi. Mannertoimitusyhtiö S.-Lla. C: n.V. 87-103.
3. Giancoli, D. 2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed. Prentice Hall. 72 - 96.
4. Hewitt, Paul. 2012. Käsitteellinen fysiikka. Viides. Ed. Pearson.38-61.
5. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen. 100 - 119.