ARC (geometria) Mitta, kaaretyypit, esimerkit

Hän keula-, Geometriassa mikä tahansa kaareva viiva yhdistää kaksi pistettä. Kaareva viiva, toisin kuin suora viiva, on se, jonka suunta on erilainen jokaisessa pisteessä. Kaaren vastakohta on segmentti, koska tämä on suora osa, joka liittyy kahteen pisteeseen.

Geometriassa yleisimmin käytetty kaari on kehäkaari. Muita yleisen käytön kaaria ovat parabolinen kaari, elliptinen kaari ja kissanarikaari. ARC -muotoa käytetään usein arkkitehtuurissa koriste -elementtinä ja rakenneelementtinä. Näin on ovien ja ikkunoiden, samoin kuin sillat ja vesijohdot.

Kuvio 1. Sateenkaari on kaareva viiva, joka liittyy kahteen pisteeseen horisontissa. Lähde: Pixabay

[TOC]

Kaari ja sen mitta

Kaaren mitta on sen pituus, joka riippuu käyrän tyypistä, joka yhdistää nämä kaksi pistettä ja niiden sijainnin.

Pyöreän kaaren pituus on yksi helpoimmista laskea, koska ympyrän koko kaaripituus tai kehä tunnetaan.

Ympyrän kehä on kaksi pilli kertaa radiosi: P = 2 π r. Tietäen tämän, jos haluat laskea pituuden s pyöreä kulmakaari α (mitattu radiansissa) ja radiossa R -, Osuutta käytetään:

(s / p) = (α / 2 π)

Sitten puhdistus s edellisen lausekkeen ja kehän korvaaminen p sen ilmaisua radiosta riippuen R -, Sinulla on:

S = (α / 2 π) p = (α / 2 π) (2 π r) = α R.

Toisin sanoen pyöreän kaaren mitta on sen kulma -aukon tuote pyöreällä kaarisäteellä.

Kaarelle yleisellä tavalla ongelma on monimutkaisempi siihen pisteeseen, että antiikin suuret ajattelijat väittivät, että se oli mahdoton tehtävä.

Se voi palvella sinua: mitkä ovat algebralliset lausekkeet ja jotka ovat yleisimpiä?

Vasta vuonna 1665 tapahtuvan differentiaali- ja kiinteälaskennan tuloksena minkä tahansa kaaren mittausongelma ratkaistiin tyydyttävästi. 

Ennen differentiaalilaskennan keksimistä vain ratkaisuja voitiin löytää käyttämällä monikulmaisia ​​linja- tai ympäryskaaria, jotka lähestyivät todellista kaaria, mutta nämä ratkaisut eivät olleet tarkkoja. 

Kaaretyypit

Geometrian kannalta kaarit luokitellaan kaarevaan linjaan, joka yhdistää koneen kaksi pistettä. Arkkitehtonisen käytön ja muodon mukaan on muita luokituksia.

Pyöreä kaari

Kun linja, joka yhdistää tason kaksi pistettä, on tietyn säteen ympäryspala, on pyöreä kaari. Kuvio 2 esittää säteen R: n pyöreän kaaren, joka yhdistää pisteet A ja B.

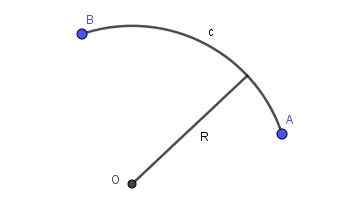Kuva 2. Radio r ympyräkaari, joka yhdistää kohta A ja B. Valmistaja: Ricardo Pérez.

Parabolinen kaari

Vertaus on suuntaus, joka seuraa esinettä, joka on heitetty ilmaan vinossa muodossa. Kun kahteen pisteeseen liittyvä käyrä on vertaus, niin kuvassa 3 on parabolinen kaari.

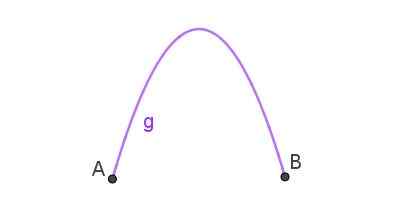Kuva 3. Parabolinen kaari, joka yhdistää pisteet A ja B. Valmistaja: Ricardo Pérez.

Tämä on muoto, joka hyväksyy vesisuihkut, jotka tulevat letkusta, joka osoittaa. Parabolinen kaari voidaan havaita vesilähteissä.

Kuva 4. Parabolinen kaari, joka on muodostettu veden lähteestä Dresdenissä. Lähde: Pixabay.

Kaari

Kissanarjakaari on toinen luonnollinen kaari. Kissanari on käyrä, joka muodostuu luonnollisesti, kun ketju tai köysi roikkuu mukavasti kahdesta erillisestä pisteestä.

Voi palvella sinua: mitkä ovat kulman elementit?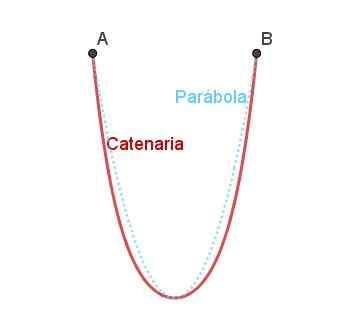 Kuva 5. Kissanarvon kaari ja vertailu paraboliseen kaareen. Valmistaja: Ricardo Pérez.

Kantanaari on samanlainen kuin Parabola, mutta se ei ole täsmälleen sama kuin se voidaan havaita kuvassa 4.

Arkkitehtuurissa käytetään käänteistä kissanarvon muotoista kaaria korkean puristuskestävyyden rakenteellisena elementtinä. Itse asiassa voidaan osoittaa, että se on vastustuskykyisin kaarityyppi kaikissa mahdollisissa muodoissa. 

Kiinteän kaaren rakentamiseksi vain köyden tai ketjun muoto kopioidaan, sitten kopioitu muoto kääntyy toistamaan sen oven lintelissä tai ikkunassa.

Elliptinen kaari

Kaari on elliptinen, jos kaksi pistettä yhdistävä käyrä on ellipsin venytys tai venymä. Ellipsi määritellään niiden pisteiden geometriseksi paikkaksi, joiden etäisyys kahteen pisteeseen annetaan aina vakion määrän.

Ellipsi on luonteeltaan ilmestyvä käyrä: se on planeetan etenemisen käyrä auringon ympärillä, kuten Johannes Kepler osoitti vuonna 1609.

Käytännössä ellipsi voidaan piirtää asettamalla kaksi tullia lattialle tai kaksi nastaa paperille ja sidottamalla niihin köyden. Sitten köysi on kireä merkinnän tai lyijykynän kanssa ja käyrä piirretään. Pala ellipsi on elliptinen kaari. Seuraava animaatio kuvaa kuinka ellipsi on piirretty:

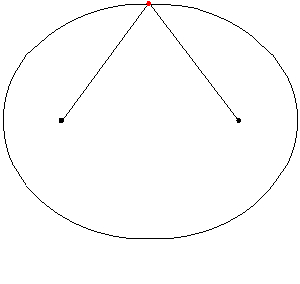Kuva 5. Ellipsin posenilla. Lähde: Wikimedia Commons

Kuvio 6 esittää elliptistä kaaria, joka yhdistää pisteet G ja H.

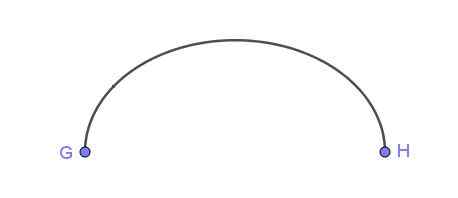Kuva 6. Elliptinen kaari, joka yhdistää kaksi pistettä. Valmistaja: Ricardo Pérez.

Esimerkkejä kaarista

Seuraavat esimerkit viittaavat siihen, kuinka joidenkin tiettyjen kaareiden kehä lasketaan.

Voi palvella sinua: Transcendent -numerot: Mitä ovat, kaavat, esimerkit, harjoitukset

Esimerkki 1

Kuvio 7 esittää ikkunan, joka on päättynyt leikkauskaariin. Kuvassa esitetyt mitat ovat jaloilla. Laske kaaren pituus.

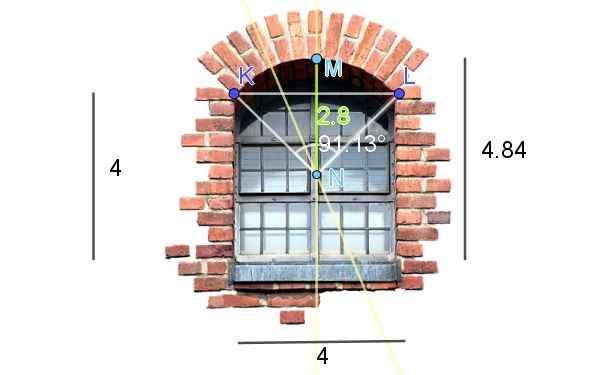Kuva 7. Ikkunan pyöreän kaaren pituuden laskeminen. (Omat merkinnät - ikkunakuva Pixabayssa)

Saadaksesi ikkunan lintelin ympyräkaaren keskusta ja säde seuraavat kuvassa tehdään seuraavat rakenteet:

-KL -segmentti piirretään ja sen mediatrix on piirretty.

-Sitten Lintelin korkein kohta sijaitsee, jota kutsumme m. KM -segmentti otetaan sitten huomioon ja sen mediatrix vedetään.

Kahden lääketieteen sieppaaminen on piste n ja on myös pyöreän kaaren keskipiste.

-Nyt sinun on mitattava NM -segmentin pituus, joka vastaa pyöreän kaaren sädettä r: r = 2.8 jalkaa.

-Tietää kaaren pituus säteen lisäksi, kaaren muodostava kulma. Joka voidaan määrittää kahdella menetelmällä tai mitataan kuljettajalla tai lasketaan vuorotellen trigonometrialla.

Kaaren muodostava kulma on 91,13º, joka on muunnettava radianiksi:

 91,13º = 91,13º * π / 180º = 1,59 radiaania

Laskemme lopulta pituuden s kaaren läpi kaavan läpi S = α R.

S = 1,59 * 2.8 jalkaa = 4,45 jalkaa

Esimerkki 2

Etsi kuvassa 8 esitetty elliptisen kaaren pituus, tunnetaan r - ja pieni puoli -akseli s ellipsi.

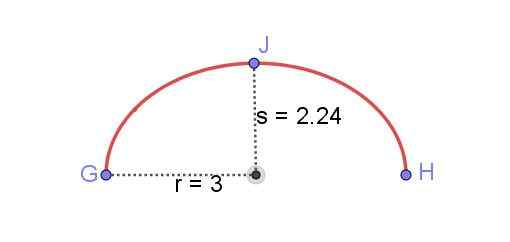Kuva 8. Elliptinen kaari GH: n välillä. Valmistaja: Ricardo Pérez.

Ellipsin pituuden löytäminen oli pitkään yksi matematiikan vaikeimmista ongelmista. Elliptisten integraalien ilmaisemia ratkaisuja voidaan saada, mutta numeerisen arvon niillä on laajennettava näitä voimasarjojen integraaleja. Tarkka tulos vaatisi näiden sarjojen äärettömiä ehtoja.

Onneksi vuosina 1887–1920 asuneen hindujen alkuperän matemaattinen nero löysi kaavan, joka lähestyy hyvin tarkkaan ellipsin kehää:

Ellipsin kehä = π [3 (r + s) - √ ((3r + s) (r + 3s))]]]]]

Ellipsin kehä, jonka r = 3 cm ja s = 2.24 cm on 16,55 cm. Eliptisellä kaarilla on kuitenkin puolet tästä arvosta:

Elliptinen kaaren pituus GH = 8.28 cm.

Viitteet

1. Clemens s. 2008. Geometria ja trigonometria. Pearson -koulutus.
2. Garcia f. Numeeriset toimenpiteet Java. Ellipsin pituus. Haettu osoitteesta: SC.Ehu.On
3. Dynaaminen geometria. Kaaret. Toipunut Geometriadinamicasta.On
4. Piza. Ellipsit ja vertaukset ympärillämme. Haettu osoitteesta: Pizaas.com
5. Wikipedia. Kaari (geometria). Palautettu: se on.Wikipedia.com