Kuution reunat

Mikä on kuution reuna?

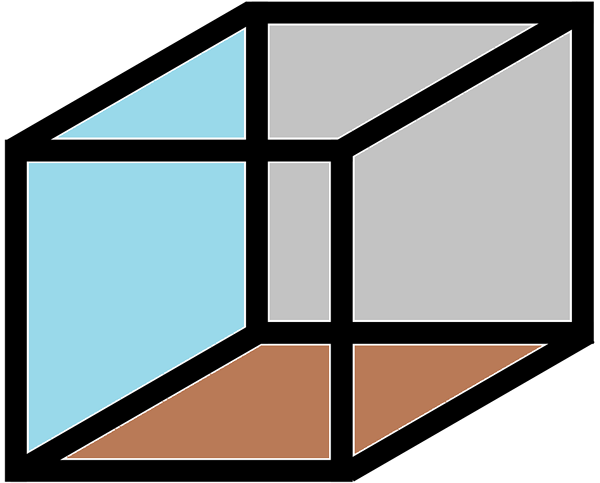
Se kuution reuna Se on sen reuna: se on linja, joka liittyy kahteen kärkeen tai kulmaan. Reuna on linja, jossa geometrisen hahmon kaksi puolta sieppataan. Kuutiossa on 12 reunaa.

Edellinen määritelmä on yleinen ja sitä sovelletaan mihin tahansa geometriseen lukuun, ei vain kuutioon. Kun kyse on tasaisesta hahmosta, reunat vastaavat mainitun luvun sivuja.

Sitä kutsutaan rinnakkain geometriseen hahmoon, jossa on kuusi pintaa rinnakkaisohjelmien muodossa, joista vastakohdat ovat yhtä suuret ja yhdensuuntaiset toistensa kanssa.

Erityisesti, jossa kasvot ovat neliömäisiä, rinnakkaiskipiä kutsutaan kuutioksi tai heksaedroksi, lukuksi, jota pidetään säännöllisenä polyhedronina.

Tapoja tunnistaa kuution reunat

Paremman kuvan saavuttamiseksi jokapäiväisiä esineitä voidaan käyttää tarkasti määrittämään kuution reunat.

1- Armando Paper-kuutio

Jos näet kuinka paperi tai pahvi kauha on rakennettu, näet mitä reunasi ovat. Se alkaa piirtää ristiä, kuten kuva ja tietyt sisäiset viivat ovat merkittyjä.

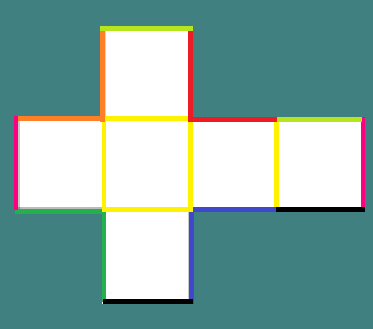
Jokainen keltainen viiva edustaa taitoa, joka on kuution reuna (reuna).

Samoin jokainen linjapari, jolla on sama väri, muodostaa reunan, kun ne liittyvät. Kaikkiaan kuutiossa on 12 reunaa.

2- Piirrä kuutio

Toinen tapa nähdä, mitkä kuution reunat ovat tarkkailla, miten se vedetään. Aloitat piirtämällä neliön sivua L; Neliön kukin puoli on kuution reuna.

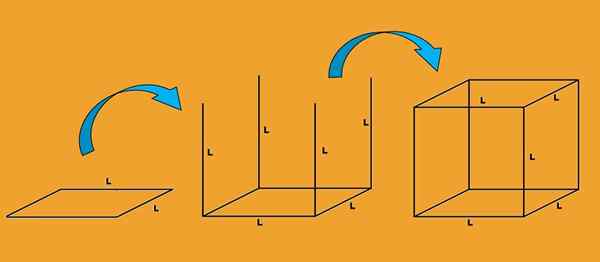
Sitten jokaisesta kärkipisteestä piirretään neljä pystysuuntaista viivaa, ja kunkin linjan pituus on l. Jokainen rivi on myös kauhan reuna.

Lopuksi piirretään toinen neliö L, siten, että sen kärkipisteet vastaavat edellisessä vaiheessa vedettyjen reunojen päätä. Tämän uuden neliön jokainen sivu on kuution reuna.

3- Rubik-kuutio

Alussa tapahtuneen geometrisen määritelmän havainnollistamiseksi näet Rubik -kuution.

Jokaisella kasvolla on eri väri. Reunoja edustaa linja, jossa kasvot siepataan eri väreillä.

Euler -lause

Eulerin Polyhedros -lause sanoo, että monikulmion ansiosta pusekkeiden lukumäärä P -lukumäärä on yhtä suuri kuin reunojen lukumäärä plus 2: een. Eli c+v = a+2.

Edellisissä kuvissa voidaan nähdä, että kuutiossa on 6 pintaa, 8 kärkeä ja 12 reunaa. Siksi se täyttää Polyhedran Euler -lauseen, koska 6+8 = 12+2.

Kuution reunan pituuden tunteminen on erittäin hyödyllistä. Jos reunan pituus tunnetaan, kaikkien sen reunojen pituus tunnetaan, mikä voi saada tietyt kuutiotiedot, kuten sen tilavuus.

Kuution tilavuus on määritelty L³: ksi, missä L on sen reunojen pituus. Siksi kuution tilavuuden tuntemiseksi on tarpeen tietää vain L: n arvo.