Matemaattinen biologian historia, opinto -kohde, sovellukset

Se Matemaattinen biologia tai biomaatematiikka on tieteen haara, joka vastaa numeeristen mallien kehittämisestä, jotka onnistuvat simuloimaan eläviin olentoihin liittyviä erilaisia ​​luonnonilmiöitä; toisin sanoen se merkitsee matemaattisten työkalujen käyttöä luonnollisten tai biologisten järjestelmien tutkimiseen.

Kuten sen nimessä voidaan ymmärtää, biomaatematiikka on monitieteinen alue, joka on biologian ja matematiikan tiedon risteyksessä. Yksinkertainen esimerkki tästä kurinalaisuudesta voisi sisältää tilastollisten menetelmien kehittämisen ongelmien ratkaisemiseksi genetiikan tai epidemiologian alueella, nimeämiseksi.

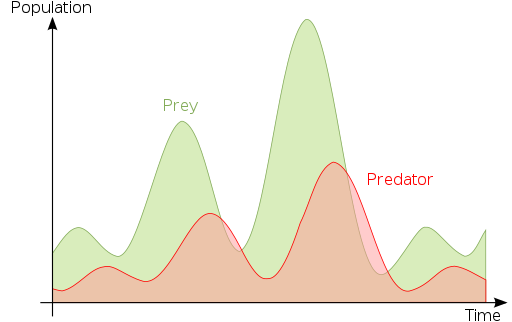Lotka-Volterran laki petoeläimien ja patojen välisestä suhteesta (lähde: Curtis Newton ↯ 10:55, 20. Huhtikuu. 2010 (CEST).Alkuperäinen lähettäjä oli Lämpel Saksan Wikipediassa. [CC BY-SA 3.0 (http: // creativecommons.Org/lisenssit/by-SA/3.0/)] Wikimedia Commonsin kautta)

Tällä tietoalueella on normaalia, että matemaattiset tulokset johtuvat biologisista ongelmista tai niitä käytetään niiden ratkaisemiseen, mutta jotkut tutkijat ovat kuitenkin onnistuneet ratkaisemaan matemaattiset ongelmat, jotka perustuvat biologisten ilmiöiden havaitsemiseen, joten se ei ole yksisuuntainen suhde Molemmat tieteen alat.

Yllä olevasta voidaan varmistaa, että matemaattinen ongelma on loppu, jolle biologisia työkaluja käytetään ja päinvastoin; että biologinen ongelma on loppu, jolle käytetään hyvin erilaisia ​​matemaattisia työkaluja.

Tällä hetkellä matemaattisen biologian kenttä kasvaa kiihtyneillä vaiheilla, ja sitä pidetään yhtenä matematiikan nykyaikaisimmista ja mielenkiintoisimmista sovelluksista. Se on erittäin hyödyllinen paitsi biologiassa, myös biolääketieteellisissä tieteissä ja bioteknologian alalla.

[TOC]

Biomaatemaryhmähistoria

Matematiikka ja biologia ovat kaksi tiedettä, joilla on moninaisuus sovelluksia. Matematiikka on ehkä yhtä vanha kuin länsimainen kulttuuri, sen alkuperä on peräisin monta vuotta, ennen.

Voi palvella sinua: Oksidaasitesti: Perusta, menettely ja käyttö

Biologia tieteenä on kuitenkin paljon uudempi, koska sen käsitteellistäminen tapahtui vasta 1800 -luvun alussa Lamarckin intervention ansiosta 1800 -luvulta.

Matemaattisen ja biologisen tiedon suhde on kapea sivilisaatioiden varhaisvaiheiden jälkeen, koska nomadisten kansojen ratkaiseminen tapahtui sen löytämisen ansiosta, että luontoa voitaisiin käyttää systemaattisesti, mikä on oltava pakollinen ensimmäiset käsitteet Matematiikka ja biologinen.

Heidän periaatteidensa mukaan biologisia tieteitä pidettiin "käsitöinä", koska ne viittasivat pääasiassa suosittuihin toimintoihin, kuten maatalouden tai karjan karjakauppaan; Samaan aikaan matematiikka löysi abstraktion ja sillä oli jonkin verran kaukana sovelluksia.

Biologian ja matematiikan välinen yhtymäkohta juontaa juurensa viidenteentoista ja kuudennentoista vuosisadan ajan fysiologian myötä, joka on tiede, joka ryhmittelee tiedon, luokittelemalla ne, tilaamalla ne ja systemaattisesti käyttävät matemaattisia työkaluja tarvittaessa tarvittaessa.

Thomas Malthus

Se oli Thomas Malthus, nykyaikainen taloustieteilijä Lamarckin kanssa, joka loi ennakkotapauksen matemaattisen biologian alkamiselle, koska hän oli ensimmäinen, joka postuloi matemaattisen mallin, joka selittää luonnonvaroihin perustuvan väestödynamiikan, joka perustuu luonnonvaroihin.

Malthuksen lähestymistavat olivat myöhemmin kehittyneempiä ja kehitettyjä, ja nykyään ovat osa ekologisten mallien perustaa, joita käytetään selittämään saalistajien ja niiden saaliin välistä suhdetta, esimerkiksi.

Matemaattisen biologian tutkimuksen kohde

Matemaattinen biologia on monitieteinen tieteellinen alue. Lähde: Konstantin Kolosov - Pixabay

Matemaattinen biologia on tiede, joka johtuu erilaisten matemaattisten työkalujen integroinnista biologisiin, kokeellisiin tai ei, joilla pyritään hyödyntämään matemaattisten menetelmien "voimaa" selittämään paremmin elävien olentojen, niiden solujen ja molekyylien maailmaa,.

Se voi palvella sinua: Ruokaketju: elementit, troofinen pyramidi ja esimerkit

Matemaattinen biologia koostuu "yksinkertaisesta" siitä, että kyseessä on kyseessä olevan teknologisen monimutkaisuuden asteesta, jonka mukaan kahden prosessin välillä on analogia, nimittäin:

- Elävän olennon monimutkainen rakenne on seurausta yksinkertaisen "kopioidun" ja "leikkaamisen ja silmukoinnin" käytöstä tai "Silmukointi”(Esimerkiksi) alkuperäiseen tietoon, joka sisältyy DNA -sekvenssiin (deoksihiohapon happo) -sekvenssiin.

- Lopputulos F (Ω) laskettavan toiminnon soveltamisesta järjestelyyn W - voidaan saada soveltamalla yksinkertaisten perustoimintojen yhdistelmää W -.

Matemaattisen biologian kenttä soveltaa matematiikan alueita, kuten laskenta, todennäköisyysteoriat, tilastot, lineaariset algebra, algebrallinen geometria, topologia, differentiaaliyhtälöt, dynaamiset järjestelmät, yhdistelmä- ja koodausteoria.

Äskettäin tätä tieteenalalla on erittäin hyväksikäytetty erityyppisten tietojen kvantitatiivista analysointia, koska biologiset tieteet ovat omistautuneet suuriin tietojoukkoihin, joista tiedot voidaan poimia arvokkaita.

Itse asiassa monet tutkijat katsovat, että biologisen tiedon suuri räjähdys "loi" tarpeen kehittää uusia ja monimutkaisempia matemaattisia malleja analysoitavaksi, samoin kuin laskennalliset algoritmit ja huomattavasti monimutkaisemmat tilastolliset menetelmät.

Sovellukset

Yksi matemaattisen biologian merkittävimmistä sovelluksista liittyy DNA -sekvenssien analysointiin, mutta tämä tiede osallistuu myös epidemioiden mallintamiseen ja hermosignaalien leviämisen tutkimiseen.

Sitä on käytetty neurologisten prosessien, kuten Parkinsonin taudin, Alzheimerin ja amyotrofisen lateraaliskleroosin, tutkimiseen.

Voi palvella sinua: Erythous: Ominaisuudet, rakenne, toiminnot

Se on erittäin hyödyllinen evoluutioprosessien (teoriointien) tutkimuksessa ja mallejen kehittämisessä, jotka selittävät elävien olentojen suhteen toisiinsa ja niiden ympäristöön, toisin sanoen ekologisiin lähestymistapoihin.

Erityyppisten syöpien mallintaminen ja simulointi on myös hyvä esimerkki monista sovelluksista, joita matemaattisella biologialla on nykyään, etenkin solupopulaatioiden välisten vuorovaikutusten simuloinnissa.

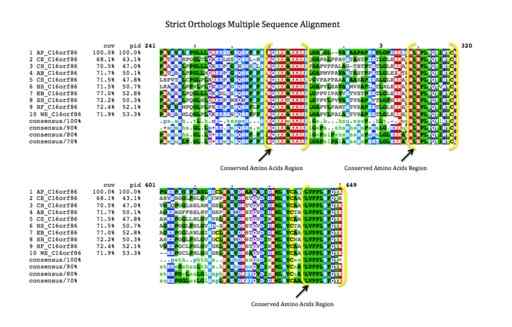Esimerkki genomiikassa yleisesti käytettyjen DNA-sekvenssien analyysistä (lähde: Radtk172 [CC BY-SA 4.0 (https: // creativecommons.Org/lisenssit/by-SA/4.0)] Wikimedia Commonsin kautta)

Biomaatematiikka on myös erittäin edistynyt laskennallisen neurotieteen alueella, populaation ja fylogenomisen ja genomisen dynamiikan tutkimuksissa yleensä.

Tässä viimeisessä genetiikan haarassa on ollut merkitystä, koska se on yksi viime vuosien korkeimmista kasvualueista, koska saatujen tietojen määrä on erittäin korkea, mikä ansaitsee uusia ja parempia tekniikoita sen käsittelyyn ja analyysiin.

Viitteet

1. Andersson, S., Larsson, k., Larsson, M., & Jacob, M. (Toim.-A. (1999). Biomaatematiikka: Bioslatuurien ja biodynamiikan matematiikka. Elsevier.
2. Elango, P. (2015). Matematiikan rooli biologiassa.
3. Friedman, a. (2010). Mikä on matemaattinen biologia ja kuinka hyödyllinen se on. AMS: n ilmoitukset, 57 (7), 851-857.
4. Hofmeyr, J. H. S. (2017). Matematiikka ja biologia. Etelä-Afrikan Journal of Science, 113 (3-4), 1-3.
5. Kari, l. (1997). DNA -tietojenkäsittely: Biologisen matematiikan saapuminen. Matemaattinen älykäs, 19 (2), 9-22.
6. Pacheco Castelao, J. M. (2000). Mikä on matemaattinen biologia?
7. Reed, m. C. (2004). Miksi Mathematico Biologia on niin kovaa? AMS: n ilmoitukset, 51 (3), 338-342.
8. S. M. (1972). Sub -ideat ja näkymät biomaattisesti. Biofysiikan ja biotekniikan vuosikatsaus, 1 (1), 277-292.