Suorakulmion ominaisuudet

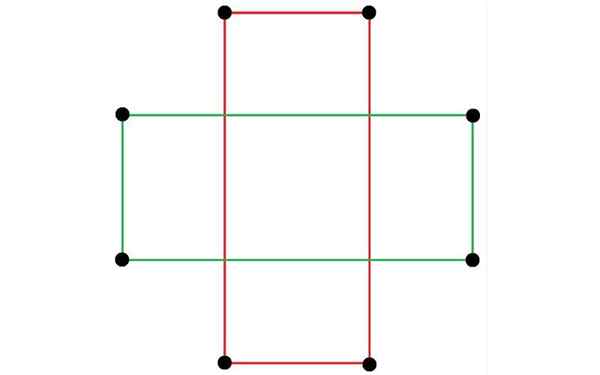
Kaksi suorakulmiota. Lähde: Tomruen, CC BY-SA 4.0, Wikimedia Commons

Hän suorakulmio Sille on ominaista olla litteä geometrinen hahmo, jolla on neljä sivua ja neljä kärkeä. Näistä neljästä sivusta yhdellä parilla on sama mitta, kun taas toisella parilla on erilainen mitta.

Tämä kuva on rinnakkainen monikulmio, koska suorakulmion vastakkaiset puolet ovat yhdensuuntaiset ja niillä on samat mitat. Suorakulmioiden muodostavien kulmien amplitudi on 90 °, joten ne ovat suorakulmia. Sieltä tulee nimi suorakulmio.

Se tosiasia, että suorakulmioissa on neljä saman amplitudin kulmaa, aiheuttaa nämä geometriset luvut kutsumaan equiángulosiksi.

Kun suorakulmio ylitetään diagonaalisella viivalla, luodaan kaksi kolmiota. Jos suorakulmio ylitetään kahdella diagonaalisella viivalla, ne ylittävät kuvan keskellä.

9 Suorakulmioiden keskeisiä ominaisuuksia

1. Sivujen lukumäärä ja ulottuvuus

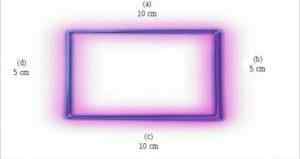
Suorakulmiot koostuvat neljästä puolesta. Voimme jakaa nämä sivut kahteen pariin: yksi sivuparit mittaavat samalla tavalla, kun taas toisella vääntömomentilla on korkeammat tai pienemmät mitat kuin edellisessä vääntömomentissa.

Vastustavilla sivuilla on samat toimenpiteet, kun taas peräkkäisillä on erilaisia ​​toimenpiteitä.

Tämän lisäksi suorakulmiot ovat kahden ulottuvuuden lukuja, mikä tarkoittaa, että niillä on vain kaksi ulottuvuutta: leveä ja korkea.

Lähde: Wikipedia.org

2. Monikulmio

Suorakulmiot ovat monikulmioita. Tässä mielessä suorakulmiot ovat geometrisia lukuja, joita rajoittaa suljettu monikulmainen viiva (ts. Suora segmentti, joka sulkeutuu sinänsä).

Tarkemmin sanottuna suorakulmiot ovat nelikulmaisia ​​monikulmioita, koska niillä on neljä puolta.

Se voi palvella sinua: Iskosceles -kolmio

3. Ne eivät ole tasa -arvoisia monikulmioita

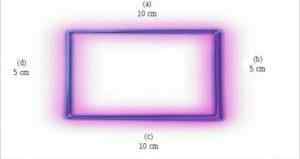
Monikulmio on tasapainossa, kun kaikki sen sivut mittaavat saman. Suorakulmion sivuilla ei ole samoja toimenpiteitä. Tästä syystä ei voida sanoa, että suorakulmiot ovat tasa -arvoisia.

Lähde: Wikipedia.org

4. Evengle Polygon

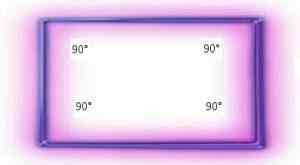
Equiángulos -polygonit ovat niitä, jotka koostuvat kulmista, joilla on sama amplitudi.

Kaikki suorakulmiot koostuvat neljästä suorasta kulmasta (ts. 90 ° kulmasta). 10 cm x 20 cm: n suorakulmiossa on neljä 90 ° kulmaa, sama tapahtuu suuremmalla tai vähemmän suorakulmiolla.

Lähde: Wikipedia.org

5. Suorakulmion alue

Suorakulmion pinta -ala on yhtä suuri kuin pohjan tuote korkeuden mukaan, pohja on vaakasuora puoli, kun taas korkeus on pystysuora puoli. Yksinkertaisempi tapa nähdä, että se on moninkertaistaa kahden vierekkäisen sivun mitat.

Tämän geometrisen hahmon pinta -alan laskemiseksi on:

a = b x a

Joitakin esimerkkejä suorakulmion alueen laskemisesta ovat:

- Suorakulmio, jonka pohja on 5 cm ja 2 cm korkeus: 5 cm x 2 cm = 10 cm²

- Suorakulmio, jonka pohja on 2 m ja korkeus 0,5 m: 2 m x 0,5 m = 2 m²

- Suorakulmio 18 m ja korkeus 15 m: 18 m x 15 m = 270 m²

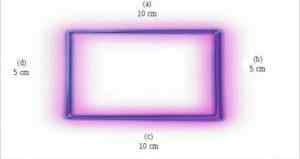Tämän suorakulmion pohja on 10 cm ja korkeus 5 cm. Alueesi on 10 cm x 5 cm tuote. Tässä tapauksessa suorakaiteen alue on 50 cm². Lähde: Wikipedia.org

6. Suorakulmiot ovat yhdensuuntaisia

Neljännekset voidaan luokitella kolmeen tyyppiin: trapetsoidit, trapetsoidit ja rinnakkaisohjelmat. Viimeksi mainituille on ominaista, että sillä on kaksi paria rinnakkaista sivua, joilla ei välttämättä tarvitse olla samoja toimenpiteitä.

Tässä mielessä suorakulmiot ovat yhdensuuntaisia ​​ohjelmia, koska kaksi paria sivua on.

Voi palvella sinua: Ensimmäisen aseman yhtälöt: kaava, kuinka ratkaista ne, esimerkki, harjoituksetLähde: Wikipedia.org

7. Vastakkaiset kulmat ovat yhdenmukaisia ​​ja peräkkäisiä täydentäviä

Vastakkaiset kulmat ovat niitä, joita löytyy kuvan ei -säilykkeistä. Vaikka peräkkäiset kulmat ovat vierekkäisiä, yksi vieressä.

Kaksi kulmaa ovat yhdenmukaisia, kun heillä on sama amplitudi. Toisaalta kaksi kulmaa on täydentävä, kun näiden amplitudien summa tuottaa 180 ° kulman tai mikä on sama, tasainen kulma.

Kaikki suorakulmion kulmat mittaavat 90 °, joten voidaan sanoa, että tämän geometrisen hahmon vastakkaiset kulmat ovat yhdenmukaisia.

Peräkkäisten kulmien suhteen suorakulmio koostuu 90 °: sta kulmasta. Jos peräkkäisiä lisätään, tulos on 180 °. Joten nämä ovat täydentäviä kulmia.

8. Se koostuu kahdesta suorakulmion kolmiosta

Jos suorakulmioon piirretään diagonaali (linja, joka kulkee suorakulmion kulmasta toiseen vastakkaiseen), saadaan kaksi suorakaiteen kolmiota. Tämäntyyppinen kolmio on sellainen, joka muodostuu suorassa kulmassa ja kahdella akuutissa kulmassa.

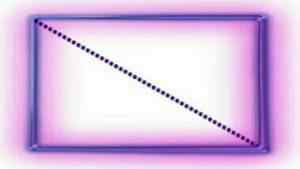Pistoviiva edustaa diagonaalia. Tämä jakaa suorakulmion kahteen kolmioon. Lähde: Wikipedia.org

9. Diagonaalit leikataan niiden keskipisteessä

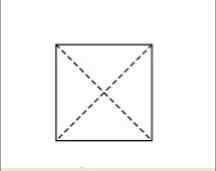
Kuten jo selitettiin, diagonaalit ovat linjoja, jotka menevät yhdestä kulmasta toiseen vastakkaiseen kulmaan. Jos suorakulmioon piirretään kaksi diagonaalia, ne ylittävät kuvan keskipisteessä.

Viitteet

1. Suorakulmio. Toipunut Mathisfunista.com.
2. Suorakulmio. Palautettu Merriam-Websteristä.com.
3. Rhombusien, suorakaiteenkertojen ja neliöiden ominaisuudet. Nukkeet toipuivat.com.
4. Suorakulmio. Haettu jstk.Wikipedia.org.
5. Suorakulmio. Toipunut Collinsdiction ja.com.

Voi palvella sinua: moninkertainen käänteinen: Selitys, esimerkit, ratkaisut harjoitukset