Aksiaalikuormitus kuinka lasketut ja ratkaistut harjoitukset

Se Aksiaalikuorma Rakenteen muodostavan elementin symmetria -akselin rinnakkain suunnataan voima. Aksiaalinen voima tai kuorma voi olla jännitys tai puristus. Jos aksiaalivoiman vaikutusviiva osuu samanaikaisesti symmetria -akselin kanssa, joka kulkee otetun elementin keskikohdan läpi, sanotaan, että se on samankeskinen aksiaalikuorma tai voima.

Päinvastoin, jos se on aksiaalinen voima tai kuorma, joka on yhdensuuntainen symmetrian akselin kanssa, mutta jonka toimintaviiva ei ole itse akselilla.

Kuvio 1. Aksiaalikuorma. Lähde: Itse tehty

Kuviossa 1 keltaiset nuolet edustavat voimia tai aksiaalikuormia. Yhdessä tapauksessa se on samankeskinen jännitysvoima ja toisessa kohtaamme eksentrisen puristusvoiman.

Aksiaalikuormituksen yksikkö kansainvälisessä järjestelmässä, jos se on Newton (n). Mutta muita voimayksiköitä, kuten kilogrammivoimaa (KG-F) ja puntalujuutta (LB-F), käytetään usein (LB-F).

[TOC]

Kuinka se lasketaan?

Aksiaalikuorman arvon laskemiseksi rakenteen elementeissä on noudatettava seuraavia vaiheita:

- Tee voimakaavio jokaisessa elementissä.

- Soveltaa yhtälöitä, jotka takaavat translaatiotasapainon, ts. Kaikkien voimien summa on mitätön.

- Harkitse vääntömomenttien yhtälöä niin, että kiertotasapaino täyttyy. Tässä tapauksessa kaikkien vääntömomenttien summan on oltava tyhjä.

- Laske voimat, samoin kuin tunnista aksiaaliset voimat tai kuormat jokaisessa elementissä.

Aksiaalikuormitussuhde normaaliin ponnisteluun

Keskimääräinen normaali pyrkimys määritellään aksiaalikuormituksen väliseksi jaettuna alueen poikkileikkauksen välillä. Normaalin ponnistelun yksiköt kansainvälisessä järjestelmässä S.Yllyttää. Ne ovat Newton neliömetrillä (N/ M²) tai Pascal (PA). Kuvio 2 kuvaa normaalin ponnistelun käsitettä selkeyden vuoksi.

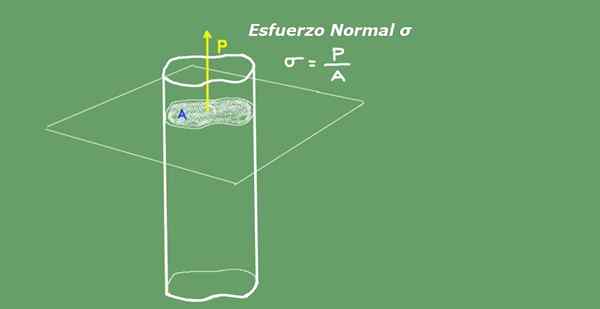Kuva 2. Normaali ponnistus. Lähde: Itse tehty.

Ratkaisut

-Harjoitus 1

Harkitse lieriömäistä betonipylvästä H ja radio r. Oletetaan, että betonin tiheys on ρ. Pylväs ei tue mitään lisäkuormaa kuin omaa painoa, ja sitä tuetaan suorakaiteen muotoisella pohjalla.

- Löydä aksiaalikuormituksen arvo pisteissä A, B, C ja D, jotka ovat seuraavissa asennoissa: a pylvään pohjassa, B A ⅓ korkeudesta h, c a ⅔ korkeudesta h ja viimeisenä D pylvään yläpäässä.

- Määritä myös keskimääräinen normaali ponnistus jokaisessa näissä paikoissa. Ota seuraavat numeeriset arvot: h = 3m, r = 20 cm ja ρ = 2250 kg/m³

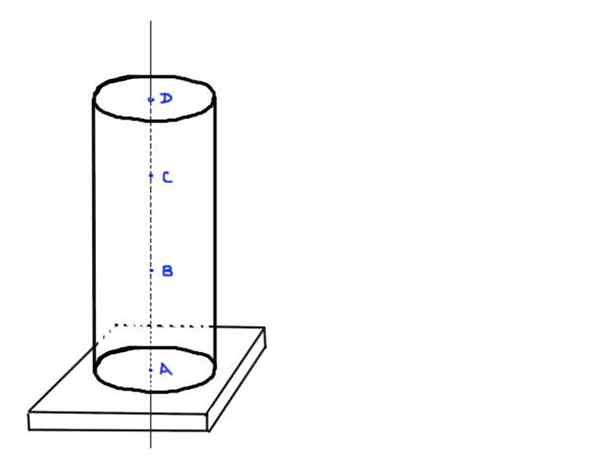Kuva 3. Lieriömäinen pylväs. Lähde: Itse tehty.

Ratkaisu

Kokonaispylväspaino

Pylvään kokonaispaino W on sen tiheyden tuote tilavuudella kerrottuna painovoiman kiihtyvyydellä:

W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 n

Aksiaalikuorma a

Pylvään pisteessä sen on tuettava koko painoa, joten aksiaalikuorma tässä vaiheessa on puristus on yhtä suuri kuin pylvään paino:

PA = W = 8313 N

Aksiaalikuorma b: ssä

Kohdassa B on yksin pylvään ⅔, joten aksiaalikuormitus on siinä vaiheessa puristus ja sen ⅔ -arvon arvon arvo:

Pb = ⅔ w = 5542 n

Kuva 3. Lieriömäinen pylväs. Lähde: Itse tehty.

Yläasennon c yläpuolella on vain sarake ⅓, joten sen aksiaalinen puristuskuorma on ⅓ oman painonsa ⅓:

PC = ⅓ W = 2771 N

Aksiaalikuorma d

Lopuksi pisteessä D, joka on pylvään yläpää, ei ole kuormaa, joten aksiaalinen voima siinä pisteessä on tyhjä.

Pd = 0 n

Normaalit ponnistelut kussakin paikassa

Kunkin aseman normaalin ponnistelun määrittämiseksi on tarpeen laskea alueen A poikkileikkaus, jonka annetaan:

A = π ∙ r² = 0,126m²

Tällä tavoin normaali ponnistus jokaisessa paikassa on aksiaalivoiman välinen osoitus jokaisessa pisteessä jaettuna jo lasketun poikkileikkauksen välillä, mikä tässä harjoituksessa on sama kaikille pisteille, koska se on sarake lieriömäinen.

σ = p/a; σa = 66,15 kPa; σb = 44,10 kPa; σc = 22,05 kPa; σd = 0,00 kPa

-Harjoitus 2

Kuva näyttää rakenteen, joka koostuu kahdesta palkista, joita kutsumme AB: lle ja CB: lle. AB -palkkia tuetaan lopussa A: lla nastaan ​​ja toiseen päähän, joka on kytketty toiseen palkkiin toisen B -pinin kautta.

Samoin CB -palkki tuetaan lopussa C nastalla ja lopussa B nasta B: n kanssa, joka yhdistää sen toiseen palkkiin. Pystysuuntainen voima tai kuorma F levitetään nastaihin B, kuten seuraavassa kuvassa esitetään:

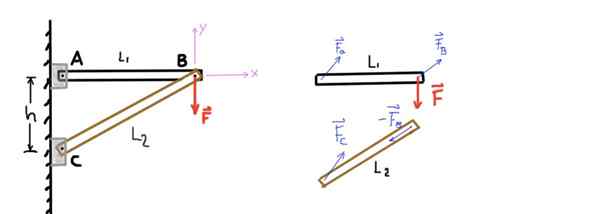Kuva 4. Kaksi palkkien rakenne ja vapaa kehon kaavio. Lähde: Itse tehty.

Oletetaan, että pylväiden paino on halveksittava, koska voima F = 500 kg-F on paljon suurempi kuin rakenteen paino. Tuken A ja C välinen ero on H = 1,5 m ja AB -palkin pituus on L1 = 2 m. Määritä aksiaalikuormitus jokaisessa tangossa, osoittaen, onko se aksiaalinen puristus vai jännitekuorma.

Ratkaisu 2

Kuva osoittaa vapaan kehon kaavion kautta rakenteen jokaiseen elementtiin vaikuttavat voimat. Cartesian -koordinaattijärjestelmä on myös osoitettu, joiden kanssa voimien tasapainoyhtälöt nostetaan.

Vääntimet tai hetket lasketaan kohtaan B ja niitä pidetään positiivisina, jos ne osoittavat näytöltä (z -akseli). Jokaisen palkin voimien ja vääntömomenttien tasapaino on:

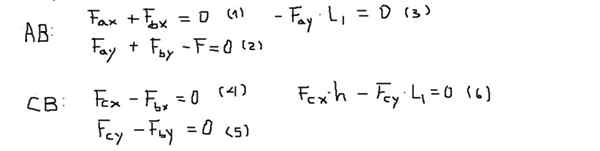
Sitten kunkin yhtälön voimien komponentit ovat selviä seuraavan järjestyksen jälkeen:

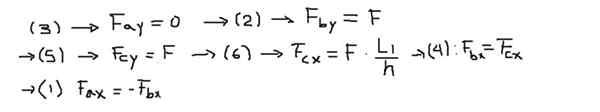
Lopuksi tuloksena olevat voimat lasketaan kunkin palkin päissä:

Voidaan huomata, että kunkin tangon päissä olevat voimat ovat yhdensuuntaisia, mikä vahvistaa, että se on aksiaalivoimia tai kuormia. AB -palkin tapauksessa se on aksiaalinen jännitevoima, jonka arvo on:

F ∙ (l1/h) = 500 kg-f ∙ (2,0m/1,5m) = 666,6 kg-f = 6533,3 n

CB -palkki on puristuksessa johtuen kahdesta voimasta, jotka toimivat heidän päähänsä, jotka ovat palkin kanssa yhdensuuntaisia ​​ja osoittavat heidän keskustaan. Aksiaalisen puristusvoiman suuruus CB -palkissa on:

F ∙ (1 + L1²/H²) 1/2 = 500 kg-F ∙ (1 + (2/1,5) ²) 1/2 = 833,3 kg-F = 8166,6 n

Viitteet

1. Olut f ... materiaalimekaniikka. Viides. Painos. 2010. MC Graw Hill. 1-130.
2. Hibbeler R. Materiaalimekaniikka. Kahdeksas painos. Prentice Hall. 2011. 3-60.
3. Gere J. Materiaalimekaniikka. Kahdeksas painos. Cengage -oppiminen. 4-220.
4. Giancoli, D. 2006. Fysiikka: sovellusten periaatteet. 6. ed. Prentice Hall. 238-242.
5. Valera Negrete, J. 2005. Yleiset fysiikan muistiinpanot. Yksinäinen. 87-98.