Yhtenäiset solujen ominaisuudet, punainen vakio ja tyypit

Se Yhtenäinen solu Se on kuvitteellinen tila tai alue, joka edustaa kokonaisuuden vähimmäisilmaisua; Että kemian tapauksessa kokonaisuus olisi kide, joka koostuu atomista, ioneista tai molekyyleistä, jotka järjestetään rakenteellisen kuvion jälkeen.

Jokapäiväisessä elämässä voit löytää esimerkkejä, jotka ilmentävät tätä käsitettä. Tätä varten on tarpeen kiinnittää huomiota esineisiin tai pintoihin, joilla on tietty toistuva järjestys sen elementteistä. Jotkut mosaiikit, bas -relef, käsityö.

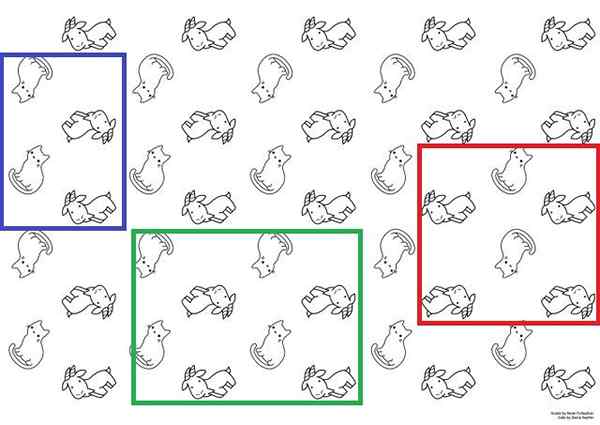Yhtenäiset solut kissassa ja vuohenpaperissa. Lähde: Hanna Petruschat (WMDE) [CC BY-SA 4.0 (https: // creativecommons.Org/lisenssit/by-SA/4.0)].

Sen selkeämmän havainnollistamiseksi sinulla on ylivoimainen kuva, jota voitaisiin käyttää kuvakudoksena. Siinä kissat ja vuohet esiintyvät kahdella vaihtoehtoisella aistella; Kissat ovat jalkoja tai päätä, ja vuohet katsovat ylös tai alas.

Nämä kissat ja vuohet luovat toistuvan rakennesarjan. Kaikkien paperin rakentamiseksi riittää toistaa yhtenäinen solu pinnan mukaan riittävästi kertoja translaatioliikkeiden avulla.

Mahdolliset yksikkösolut on esitetty sinisellä, vihreällä ja punaisella laatikoilla. Mitä tahansa näistä kolmesta voitaisiin käyttää paperin saamiseen; Mutta on välttämätöntä siirtää niitä mielikuvituksellisesti pintaa pitkin selvittääksesi, toistaako ne saman kuvan havaitun sekvenssin.

Punaisesta laatikosta alkaen olisi ymmärrettävä, että jos kolme saraketta (kissoja ja vuohia) siirrettäisiin vasemmalle, kaksi vuohia ei enää ilmesty sen alaosaan, mutta vain yksi. Siksi se johtaisi toiseen sekvenssiin, eikä sitä voida pitää yksikkösoluna.

Vaikka ne liikkuvat mielikuvituksellisesti kaksi laatikkoa, sininen ja vihreä, sama paperisekvenssi saadaan. Molemmat ovat yksikkösoluja; Sininen laatikko kuitenkin noudattaa määritelmää enemmän, koska se on pienempi kuin vihreä laatikko.

[TOC]

Yksikkösolujen ominaisuudet

Hänen oma määritelmänsä äskettäin selitetyn esimerkin lisäksi selventää useita sen ominaisuuksia:

-Jos ne liikkuvat avaruudessa, suunnasta riippumatta, täydellinen kiinteä tai lasi saadaan. Tämä johtuu siitä, että kuten kissojen ja vuohien kanssa mainittiin, ne toistavat rakennesekvenssin; joka on yhtä suuri kuin toistuvien yksiköiden alueellinen jakauma.

-Niiden on oltava mahdollisimman pieniä (tai pienellä tilavuudella) verrattuna muihin mahdollisiin soluvaihtoehtoihin.

Voi palvella sinua: metyylimalonihappo: rakenne, ominaisuudet, synteesi, käyttää

-Ne ovat tavallisia, symmetrisiä. Samoin sen symmetria heijastuu kirjaimellisesti yhdisteen kiteisiin; Jos suolan yksikkösolu on kuutio, sen kiteet ovat kuutiometriä. Yksikkösoluilla on kuitenkin kuvattu kiteisiä rakenteita vääristyneillä geometrioilla.

-Ne sisältävät toistuvat yksiköt, jotka voidaan korvata pisteillä, mikä puolestaan ​​on kolmen dimensiona, mitä kutsutaan hiuskappaleena. Edellisessä esimerkissä kissat ja vuohet edustavat retikulaarisia pisteitä korkeammasta tasosta; eli kaksi ulottuvuutta.

Toistuvien yksiköiden lukumäärä

Yksikkösolujen toistuvat yksiköt tai retikulaariset pisteet ylläpitävät saman osuuden kiinteistä hiukkasista.

Jos kissojen ja vuohien lukumäärä lasketaan sinisen laatikon sisällä, siellä on kaksi kissaa ja vuohia. Sama pätee vihreään laatikkoon ja myös punaisella laatikolla (vaikka jo tiedetään, että se ei ole yksikkökenno).

Oletetaan esimerkiksi, että kissat ja vuohet ovat vastaavasti atomeja G ja C (outo eläinhitsaus). Koska G: n ja C: n välinen osuus on 2: 2 tai 1: 1 sinisessä laatikossa, voidaan odottaa ilman virheitä, että kiinteistöllä on GC (tai CG) kaava.

Kun kiinteistöllä on enemmän tai vähemmän kompakteja rakenteita, kuten suoloja, metalleja, oksideja, sulfideja ja seoksia, yksikkösoluissa ei ole kokonaisia ​​toistuvia yksiköitä; Eli niistä on annoksia tai osia, jotka lisäävät yhden tai kaksi yksikköä.

Näin ei ole GC: n kohdalla. Jos sininen laatikko "alkaisi" kissoille ja vuohille kahdessa (1/2G ja 1/2C) tai neljässä osassa (1/4G ja 1/4C). Seuraavissa osissa nähdään, että näissä yksikkösoluissa retikulaariset kohdat jaetaan kätevästi tällä ja muilla tavoilla.

Mitkä verkkovakiot määrittelevät yksikkösolun?

GC -esimerkin yhtenäiset solut ovat kaksiulotteisia; Tätä ei kuitenkaan sovelleta todellisissa malleissa, joissa tarkastellaan kolmea ulottuvuutta. Siten laatikot tai rinnakkaisgrammit transformoituna rinnakkaispääniksi. Nyt termi "solu" on suurempi merkitys.

Näiden solujen tai rinnakkaiskipien mitat riippuvat siitä, kuinka kauan niiden vastaavat sivut ja kulmat ovat.

Alemmassa kuvassa on rinnakkaiskipien alakulma, joka koostuu sivuista -lla, b - ja c, ja kulmat α, β ja y.

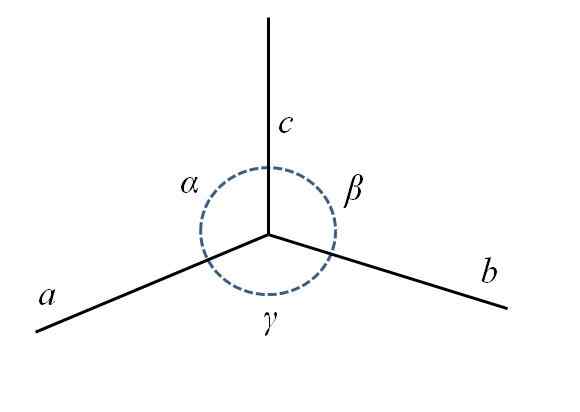Yksikkösolun parametrit. Lähde: Gabriel Bolívar.

Kuten näet, -lla on vähän pidempi kuin b - ja c. Keskustassa sinulla on ympyrä katkoviivalla, joka osoittaa kulmat α, β ja y, välillä Ac, Cb ja ba, vastaavasti. Jokaiselle yksikkökennolle näillä parametreilla on vakioarvoja ja määrittele niiden symmetria ja muu lasi.

Voi palvella sinua: Kalsiumperoksidi (CAO2): Ominaisuudet, riskit ja käytöt

Kuvaparametrit määrittelisivät uudelleen jonkin verran mielikuvitusta, kaltaisen solun kuin venytetty kuutio sen reunalla -lla. Siten yksikkösolut syntyvät reunojen eri pituuksilla ja kulmilla, jotka voidaan myös luokitella erityyppeiksi.

Kaverit

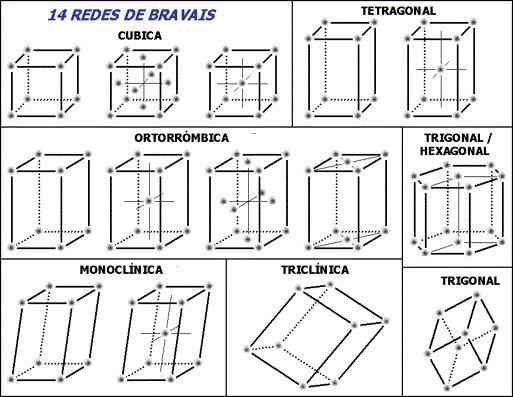
14 Bravais -verkkoa ja seitsemän kiteistä perusjärjestelmää. Lähde: Alkuperäinen lataus oli Angrense Portugalin Wikipediassa. [CC BY-SA 3.0 (http: // creativecommons.Org/lisenssit/by-SA/3.0/]]

Huomaa, että katkoviivat yksikkösolujen sisällä: ne osoittavat alemman takakulman, kuten selitetään. Seuraava kysymys voidaan kysyä, missä ovat retikulaariset kohdat tai toistuvat yksiköt? Vaikka ne antavat väärän vaikutelman, että solut ovat tyhjiä, heidän kärkipisteissä vastaus on.

Nämä solut luodaan tai valitsevat siten, että niiden kärjessä toistuvat yksiköt sijaitsevat (kuvan harmaat kohdat). Edellisessä osassa määritettyjen parametrien arvoista riippuen jokaiselle yksikkökennolle vakiona seitsemän kiteistä järjestelmää on johdettu.

Jokaisella kiteisessä järjestelmässä on oma yhtenäinen solu; Toinen määrittelee ensimmäisen. Yläkuvassa on seitsemän laatikkoa, jotka vastaavat seitsemää kiteistä järjestelmää; tai vähän enemmän yhteenvetoa, kiteisiä verkkoja. Siten esimerkiksi kuutioyksikkökenno vastaa yhtä kiteisestä järjestelmästä, joka määrittelee kuutiomaisen kiteisen verkon.

Kuvan mukaan kiteiset järjestelmät tai verkot ovat:

-Kuutio-

-Tetragonaali

-Ortorrombica

-Kuusikulmainen

-Monokliininen

-Trikliininen

-Trigonaalinen

Ja näissä kiteisissä järjestelmissä muut, jotka muodostavat neljätoista Bravaisin verkkoa; että kaikista kiteisistä verkoista ne ovat perusteellisimpia.

Kuutio-

Kuutiossa kaikki sen sivut ja kulmat ovat samat. Siksi seuraava on täyttynyt tässä yksikkösolussa:

-lla = b - = c

α = β = γ = 90º

Kuubisia yksikkösoluja on kolme: yksinkertainen tai primitiivinen, keskittynyt vartaloon (BCC) ja keskittynyt kasvoihin (FCC). Erot ovat siinä, kuinka pisteet (atomit, ionit tai molekyylit) ja niiden lukumäärät jakautuvat.

Mikä näistä soluista on kompakti? Se, jonka tilavuus on enemmän pisteitä: kuutio keskittyy kasvoihin. Huomaa, että jos korvaamme pisteet alun kissoilla ja vuohilla, ne eivät rajoittuisi yhteen soluun; Ne kuuluvat ja ne jakavat useita. Jälleen se olisi osia g tai c.

Se voi palvella sinua: hydrokoloidi

Yksiköiden lukumäärä

Jos kissat tai vuohet olisivat kärkipisteissä, ne jakaisivat 8 yksikkösolua; Eli jokaisella solulla olisi 1/8 g tai c. Yhdessä tai kuvittele 8 kuutiota, kahdessa kahdessa rivin sarakkeessa, sen visualisoimiseksi.

Jos kissat tai vuohet olisivat kasvoilla, ne jakaisivat vain 2 yksikkösolua. Nähdäksesi se riittää keräämään kaksi kuutiota.

Toisaalta, jos kissa tai vuohi olisivat kuution keskellä, ne kuuluvat vain yhteen yhtenäiseen soluun; Sama tapahtuu pääkuvan laatikoiden kanssa, kun käsitettä käsiteltiin.

Sanoi sitten yllä, yksinkertaisessa kuutiosolussa eräs Yksikkö tai retikulaarinen piste, koska siinä on 8 kärkeä (1/8 x 8 = 1). Kuubisolulle, joka on keskittynyt rungossa, sinulla on: 8 kärkeä, jotka ovat atomia, ja keskellä oleva piste tai yksikkö; Siksi on kaksi yksiköt.

Ja kuutiosoluun, joka on keskittynyt kasvoihin, joissa sinulla on: 8 kärkeä (1) ja kuusi kasvot, joissa jaetaan, missä puolet jokaisesta pisteestä tai yksiköstä on jaettu (1/2 x 6 = 3); Siksi sillä on neljä yksiköt.

Tetragonaali

Samanlaisia ​​kommentteja voidaan tehdä tetragonaalisen järjestelmän yhtenäisen solun suhteen. Sen rakenneparametrit ovat seuraavat:

-lla = b - ≠ c

α = β = γ = 90º

Ortorrombica

Ortorromisten solujen parametrit ovat:

-lla ≠ b - ≠ c

α = β = γ = 90º

Monokliininen

Monokliinisen solun parametrit ovat:

-lla ≠ b - ≠ c

α = γ = 90º; β ≠ 90º

Trikliininen

Trikliinisolun parametrit ovat:

-lla ≠ b - ≠ c

α ≠ β ≠ γ ≠ 90º

Kuusikulmainen

Kuusikulmaisen solun parametrit ovat:

-lla = b - ≠ c

α = β = 90º; γ ≠ 120º

Oikeastaan ​​solu muodostaa kuusikulmaisen prisman kolmannen osan.

Trigonaalinen

Ja lopuksi, trigonaalisen solun parametrit ovat:

-lla = b - = c

α = β = γ ≠ 90º

Viitteet

1. Whitten, Davis, Peck & Stanley. (2008). Kemia. (8. ed.-A. Cengage Learning P 474-477.
2. Shiver & Atkins. (2008). Epäorgaaninen kemia. (Neljäs painos). MC Graw Hill.
3. Wikipedia. (2019). Primitiivinen solu. Haettu: vuonna.Wikipedia.org
4. Bryan Stephanie. (2019). Yksikkökenno: Latice -parametrit ja kuutiorakenteet. Opiskelu. Toipunut: Opiskelu.com
5. Akateeminen resurssikeskus. (S.F.-A. Kristallirakenteet. [PDF]. Illinoisin teknillinen instituutti. Haettu: Web.iit.Edu
6. Belford Robert. (7. helmikuuta 2019). Kideleikkaus ja yksikkösolut. Kemian librettexts. Palautettu: Chem.Librettexts.org