Painopisteominaisuudet, laskelmat, esimerkit

Hän painovoima mitattavan kokoinen runko on kohta, jossa sen painoa pidetään levitettävänä. Siksi se on yksi staattisen ensisijaisista käsitteistä.

Ensimmäinen lähestymistapa perusfysiikan ongelmiin on olettaa, että mikä tahansa esine käyttäytyy tiettynä massana, ts. Siinä puuttuu mitat ja koko massa on keskittynyt yhteen pisteeseen. Tämä pätee laatikkoon, autoon, planeetalle tai subatomiselle hiukkaselle. Tämä malli tunnetaan nimellä hiukkasmalli.

Kuvio 1. Korkeudella hyppäävät urheilija kiinnittää ne niin, että sen painopiste on vartalon ulkopuolella. Lähde: Pixabay

Luonnollisesti tämä on lähestymistapa, joka antaa erittäin hyviä tuloksia monille sovelluksille. Ei ole helppo tehtävä harkita tuhansien ja miljoonien hiukkasten yksilöllistä käyttäytymistä, joita mikä tahansa esine voisi sisältää.

Asioiden todelliset mitat olisi kuitenkin otettava huomioon, jos haluat. Koska olemme yleensä maan välittömässä läheisyydessä, minkä tahansa kehon aina läsnä oleva voima on juuri paino.

[TOC]

Näkökohdat painopisteen löytämiseksi 

Jos kehon koko otetaan huomioon, missä painoa käytetään erityisesti? Kun sinulla on jatkuva esine mielivaltaisesti, sen paino on a Hajautettu voima kunkin sen ainesosan hiukkasen välillä.

Anna näiden hiukkasten m₁, m₂, m₃… Jokainen heistä kokee vastaavan gravitaatiovoimansa m₁g, m₂g, m₃G ..., kaikki rinnakkain. Näin on, koska maan gravitaatiokenttää pidetään vakiona suurimmassa osassa tapauksista, kun otetaan huomioon, että esineet ovat pieniä verrattuna planeetan kokoon ja ovat lähellä pintaa.

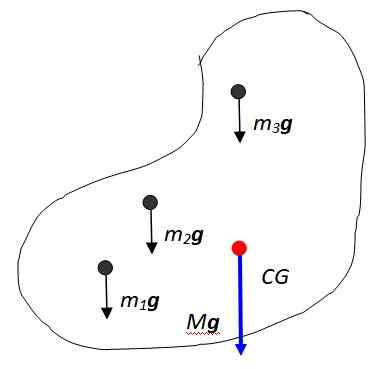Kuva 2. Kohteen paino on hajautettu massa. Lähde: Itse tehty.

Näiden voimien vektorisumma johtaa esineen painoon, jota kohdistetaan pisteeseen, jota kutsutaan kuviossa merkittynä painopisteeksi, joka sitten on samanaikainen Massakeskus. Massikeskus puolestaan ​​on kohta, jossa koko massaa voidaan pitää tiivistyneinä.

Tuloksena olevalla painolla on suuruusluokkaa Mg missä M Se on esineen kokonaismassa, ja tietysti se on suunnattu pystysuoraan kohti maan keskustaa. Sumory -merkintä on hyödyllinen kehon kokonaismäärän ilmaisemiseksi:

Symmetriset ja homogeeniset esineet, jotka vastaavat niiden tiheyttä on tasainen, on niiden painopiste geometrisessä keskuksessa: kuutiot, rinnakkaiskipit, renkaat, renkaat tai pallot.

Painopiste ei aina vastaa materiaalista pistettä. Esimerkiksi vanteen CG on sen geometrisessä keskuksessa, jossa itse taikinaa ei ole. Silti, jos haluat analysoida vannessa toimivia voimia, paino on sovellettava tähän tarkkaan kohtaan.

Missä tapauksissa, joissa esine on mielivaltainen, jos se on homogeeninen, sen massikeskus voidaan silti laskea etsimällä keskikohtaa o Kuvan baricentro.

Voi palvella sinua: Elohopea (planeetta)

Kuinka painopiste lasketaan?

Periaatteessa, jos painopiste (CG) ja massikeskus (CM) ovat samat, kun painovoimakenttä on tasainen, CM voidaan laskea ja käyttää sitä painoa.

Harkitse kahta tapausta: ensimmäinen on yksi, jossa massajakauma on huomaamaton; Eli voit laskea jokaisen järjestelmän muodostavan massan ja määrittää numeron I, kuten edellisessä esimerkissä tehtiin.

Massan keskuksen koordinaatit erillisen massajakauman suhteen ovat: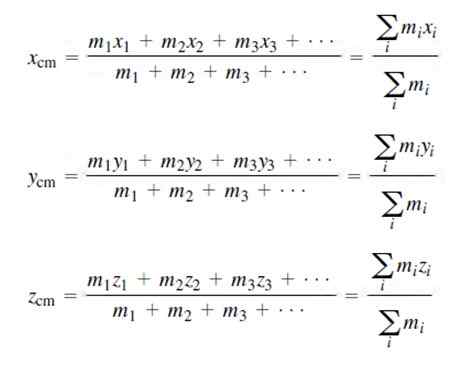

Luonnollisesti kaikkien massojen summa vastaa M -järjestelmän kokonaismassaa, kuten edellä on osoitettu.

Kolme yhtälöä pelkistetään kompaktiin muotoon ottaen huomioon vektori r_cm o Massikeskuksen sijaintivektori:

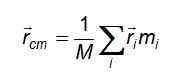
Ja jatkuvan massan jakautumisen tapauksessa, jossa hiukkaset ovat differentiaalikokoisia ja niitä ei voida erottaa niiden laskemisesta, summa korvataan integraalilla, joka tehdään kyseisen esineen miehittämälle tilalle:

Missä r - Se on differentiaalimassan sijaintivektori Dm Ja massan tiheyden määritelmä massaeron ilmaisemiseksi on tehty Dm sisältävät tilavuuserot DV-

Kohteen tiheys voi olla vakio, jolloin se tulee pois integraalista tai alueellisten koordinaattien funktiona, ja meidän on tiedettävä sen riippuvuus (x, y, z) integroinnin ratkaisemiseksi.

Ominaisuudet

Joitakin tärkeitä näkökohtia massikeskuksesta ovat seuraavat:

- Vaikka positioiden määrittämiseen tarvitaan vertailujärjestelmää, massan keskipiste ei riipu järjestelmästä tehdystä valinnasta, koska se on objektin ominaisuus.

- Kun esineellä on akseli tai symmetriataso, massakeskus on mainitulla akselilla tai tasolla. Hyödynnä tämä seikka säästää laskenta -aikaa.

- Kaikki esineeseen vaikuttavat ulkoiset voimat voidaan soveltaa massakeskukseen. Tämän pisteen seuran seuraaminen antaa globaalin kuvan esineen liikkeestä ja helpottaa sen käyttäytymisen tutkimuksen työtä.

-Kehon painopisteen löytäminen staattisessa tasapainossa

Oletetaan, että edellisen luvun runko on staattisessa saldossa.

Kuva 3. Kaavio painon vääntömomentin laskemiseksi pisteeseen tai.

Kuvan 3 mukaan verkon vääntöhetki O: n suhteen on: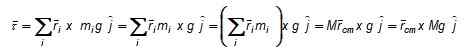Voima F levitettiin pystysuoraan painopisteeseen (tai myös sen läpi kulkevan akselin ylä- tai ala- tai ala-. F: n suuruus valitaan siten, että objektia ei myöskään siirretä, ja tällä tavalla meillä on se staattisessa tasapainossa.

Voi palvella sinua: aaltoileva optiikka

-Ratkaistu esimerkki

Ohuen tasaisen materiaalin palkin pituus on 6 m ja painaa 30 N. Sen lopussa 50 N länsi ja toinen 20 N oikeassa päässä on ripustettu. Etsi: a) Pylvään tasapainon ylläpitämiseksi tarvittavan nousevan voiman suuruus, b) sarjan painopiste.

Ratkaisu

Voiman kaavio on esitetty seuraavassa kuvassa. Pylvään paino on painopisteessä, joka vastaa sen geometristä keskustaa. Pylvään ainoa ulottuvuus on sen pituus, koska lausunto ilmoittaa, että se on ohut.

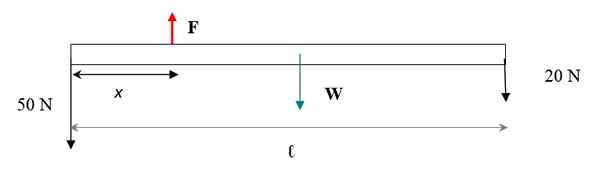Kuva 4. Pàra la Barra -kaavio.

Jotta palkki + painojärjestelmä pysyy käännöstasapainossa, voimien summan on oltava tyhjä. Voimat ovat pystysuorat, jos harkitsemme merkkiä + ja alas merkinnällä - sitten: sitten:

F-50- 20-30 N = 0

F = 100 n

Tämä voima takaa käännöksen tasapainon. Kaikkien voimien vääntymisen hetket akselista, joka kulkee järjestelmän vasemman pään läpi, ja määritelmän soveltaminen:

t = r x f

Kaikkien näiden voimien hetket valitun pisteen suhteen ovat kohtisuorassa palkin tasoon nähden:

t_F = xf = 100x

t_{W -} = -(l/2) mg = -3m . 30 n = -90 N.m

t₁ = 0 (Koska 50 N: n voima kulkee valitun kääntöakselin läpi eikä käytä hetkeä)

t₂ = -Lf₂ = 6 m . 20 n = -120 N.m

Siksi:

100 x -90 -120 N.M = 0

x = 2.10 m

Pistorasian + painon painopiste sijaitsee 2.10 metrin päässä palkin vasemmasta päästä.

Ero massakeskuksen kanssa

Painovoimakeskus on samanaikainen massan keskipisteessä, kuten osoitetaan, niin kauan kuin maan painovoimakenttä on vakiona otettavan esineen kohteille. Maan gravitaatiokenttä ei ole muuta kuin g = 9.8 m/s² Pystysuoraan suuntautuva.

Vaikka G -kokemusten arvo on leveys- ja korkeusvariaatioita, ne eivät yleensä vaikuta esineisiin, joihin useimmiten käsitellään. Hyvin erilainen olisi, jos sitä pidetään suurena ruumiina maan läheisyydessä, esimerkiksi asteroidi, joka lähellä planeettaa.

Asteroidilla on oma massakeskus, mutta sen painopisteen ei enää tarvitse olla samanaikaisesti tämän jälkeen, koska g Se todennäköisesti kokenut merkittäviä vaihteluita, kun otetaan huomioon asteroidin koko ja että kunkin hiukkasen painot eivät välttämättä ole yhdensuuntaisia.

Toinen perustavanlaatuinen ero on, että massan keskipiste on riippumatta siitä, onko esineeseen kohdistuva voima, jota kutsutaan sovellettuna painoksi. Se on objektin luontainen ominaisuus, joka paljastaa kuinka sen massa on jaettu suhteessa sen geometriaan.

Voi palvella sinua: mikä on dielektrinen vakio?

Massikeskus on molemmat, jos painoa käytetään ikään kuin ei. Ja sijaitsee samassa asennossa, vaikka esine siirretään toiselle planeetalle, jolla gravitaatiokenttä on erilainen.

Toisaalta painopiste liittyy selvästi painon soveltamiseen, kuten olemme pystyneet arvostamaan aiempia kappaleita.

Painovoimakeskuksen esimerkit

Epäsäännöllisten esineiden painopiste

On erittäin helppo selvittää, missä epäsäännöllisen esineen painopiste on kuin kuppi. Ensin se on ripustettu mistä tahansa pisteestä ja sieltä vedetään pystysuora viiva (kuvassa 5 se on Fuksia -viiva vasemmassa kuvassa).

Sitten se ripustetaan toisesta pisteestä ja vedetään uusi pystysuora (turkoosi oikeassa kuvassa). Molempien viivojen leikkauspiste on kupin painopiste.

Kuva 5 . CG -kupin sijainti. Lähde: Muokattu Pixabay.

Esineiden tasapaino

Analysoidaan tien varrella kiertävän kuorma -auton vakautta. Kun painopiste on kuorma -auton pohjan yläpuolella, se ei kaada. Vasemmalla oleva kuva on vakain sijainti.

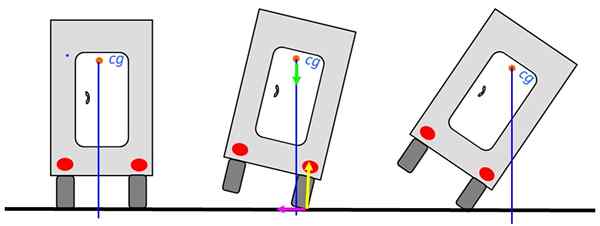Kuva 6. Kuorma -autojen tasapaino. Lähde: Itse tehty.

Jopa silloin, kun kuorma -auto nojaa oikealle, voi palata vakaaseen tasapainoasentoon, kuten väliaineen piirtämisessä, koska pystysuora kulkee edelleen pohjan läpi. Kuitenkin, kun tämä linja kulkee kuorma -auton ulkopuolelle.

Kaavio näyttää tukikohdan voimat: normaali keltainen, paino vihreänä ja staattinen kitka vasemmalla fuksiassa. Normaali ja hiero. Siksi he eivät osallistu kuorma -auton kaatopaikkaan.

Paino on edelleen, joka käyttää vääntöhetkiä, onneksi anti -Horary -mielessä ja jolla on taipumus palata kuorma -autoon tasapainoonsa. Huomaa, että pystysuora viiva kulkee tukipinnan läpi, joka on rengas.

Kun kuorma -auto on äärimmäisen oikeanpuoleisen asennossa, painon vääntymisen aika muuttuu ja muuttuu kireään suuntaan. Kuorma -auto kaataa.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.  247-253.
2. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6. ... Ed Prentice Hall. 229-238.
3. Resnick, r. (1999). Fyysinen. Osa. 1. 3. ed. espanjaksi. Mannertoimitusyhtiö S.-Lla. C: n.V. 331-341.
4. Rex, a. 2011. Fysiikan perusteet. Pearson.146-155.
5. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.340-346.