Sekoitettu sähköpiiri

Selitämme, mikä on sekoitettu piiri, sen ominaisuudet, osat, symbolit ja annamme useita esimerkkejä

Mikä on sekoitettu piiri?

Hän sekoitettu sähköpiiri Se sisältää elementit, jotka on kytketty sekä sarjaan että rinnakkain, niin että piiri suljettaessa jokaisessa niistä on muodostettu erilaisia ​​jännitteitä ja virtauksia.

Piirit on suunniteltu monenlaisilla tavoitteilla ja niiden elementit kuuluvat kahteen luokkaan: omaisuus ja velat.

Piirin aktiiviset elementit ovat generaattoreita tai jännitteitä tai virtalähteitä, suoria tai vaihtoehtoisia. Toisaalta passiiviset elementit ovat vastus, kondensaattorit tai kondensaattorit ja kelat. Sekä että muut myöntävät yhteydet sarjassa ja rinnakkain, samoin kuin näiden yhdistelmät.

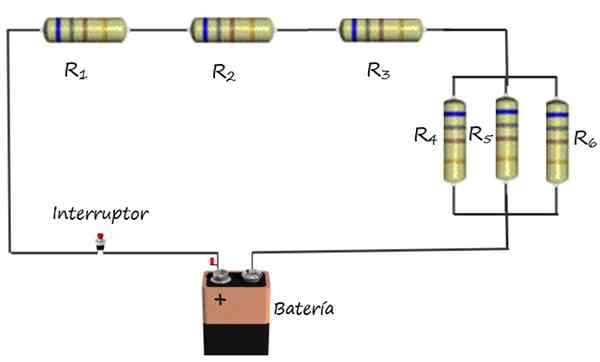
Yläkuvio näyttää esimerkiksi sähkövastusten sekoitetun assosiaation akun ja kytkimen kanssa. Resistanssit r₁, R -₂ ja r₃ Ne liittyvät sarjaan, kun taas R -vastukset₄, R -₅ ja r₆ Ne on kytketty rinnakkain.

Muita mahdollisia yhteyksiä, jotka eroavat sarja-selkäyhdistyksistä, ovat delta (tai kolmio) ja tähti, jota käytetään usein sähkökoneilla.

Sekapiirin ominaisuudet

Yleensä seuraavaa havaitaan sekoitetussa piirissä:

• Piirisyöttö voi tapahtua suoran generaattorin (akku) tai vaihtoehtoisen kautta.
• Erilaisia ​​elementtejä yhdistävät kaapelit tai johdot eivät tarjoa nykyistä vastustusta.
• Sekä jännite että virta voivat olla vakio tai muuttuva ajassa. Iskemiä kirjaimia käytetään vakioarvojen ja pienten kirjaimien merkitsemiseen, kun muuttuja.
• Puhtaasti resistiivisissä sekoitetuissa piireissä sarja sarjankestävyyksien kautta on sama, kun taas rinnakkaiskestävyydet ovat yleensä erilaisia. Virran ja jännitteen laskemiseksi kunkin resistanssin läpi piiri pelkistetään yleensä ainutlaatuiseksi vastusksi, jota kutsutaan vastaavaksi vastus- tai r_Eq .

Se voi palvella sinua: vektorisuunta: graafinen menetelmä, esimerkit, harjoitukset

Sarjankestävyydet

Rinnakkaiset vastukset

• Jos piiri koostuu N -kondensaattoreista, kun vastaava kapasitanssi C liittyy sarjaan_Eq tulos:

Sarjan kondensaattorit

Rinnakkaiskondensaattorit

• Kelat tai induktorit noudattavat samoja assosiaatiosääntöjä kuin vastarinta. Siten, kun haluat vähentää sarjan kela -assosiaatiota vastaavan induktanssin l hankkimiseksi_Eq, Käytetään seuraavia kaavoja:

Sarjan induktorit

Induktorit rinnakkain

• Sekoitettujen piirien ratkaisemiseksi vastusten kanssa, Ohm -laki ja Kirchoffin lakeja käytetään. Yksinkertaisissa resistiivisissä piireissä Ohmin laki riittää, mutta monimutkaisemmille verkkoille se on välttämätöntä läsnä.

Jännitteen ja virran välinen suhde

Piirielementistä riippuen, jännitteen tai jännitteen välillä elementin kautta sen läpi kulkevan virran voimakkuuden kanssa:

Resistenssi r

Ohmin lakia käytetään:

v_{R -}(t) = r ∙ i_{R -}(T)

Kondensaattori c

Induktanssi L

Sekapiirin osat

Sähköpiirissä seuraavat osat erottuvat:

Solmu

Union -piste kahden tai useamman johtavan johdon välillä, jotka yhdistävät piirin aktiiviset tai vastuut.

Haara

Elementit, aktiiviset tai velat, jotka ovat kahden peräkkäisen solmun välillä.

Keikari

Piirin suljettu osa kulki kulkematta kahdesti saman pisteen läpi. Sillä voi olla jännite- tai virrangeneraattori.

Kirchoff -lait tai säännöt

Kirchoff -sääntöjä sovelletaan sekä virroihin että jännitteisiin vakiona vai ovatko ne riippuvaisia ​​ajasta. Vaikka niitä kutsutaan yleensä lakeiksi, ne ovat tosiasiallisesti sääntöjä säilyttämisperiaatteiden soveltamiseksi sähköpiireihin.

Voi palvella sinua: Solid State Fysiikka: Ominaisuudet, rakenne, esimerkit

Ensimmäinen sääntö

Se vahvistaa kuorman säilyttämisen periaatteen huomauttaen, että solmuon siirtyvien nykyisten intensiteettien summa, mikä vastaa siitä tulevien intensiteettien summaa:

∑ i_{Sisäänkäynti} = ∑ i_poistuminen

Toinen sääntö

Tässä yhteydessä vahvistetaan energiansäästöperiaate, kun siinä todetaan, että jännitteiden algebrallinen summa suljetussa piirissä (mesh) on nolla.

∑ vi = 0

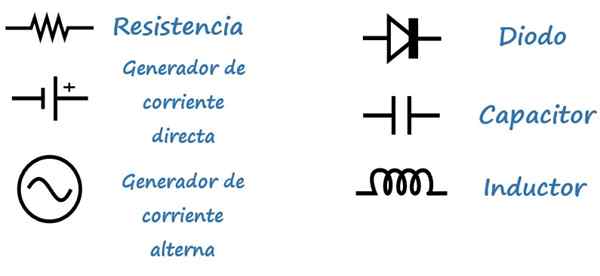
Symbolit

Piirien analysoinnin helpottamiseksi käytetään seuraavia symboleja:

Sekapiiri -esimerkit

Esimerkki 1

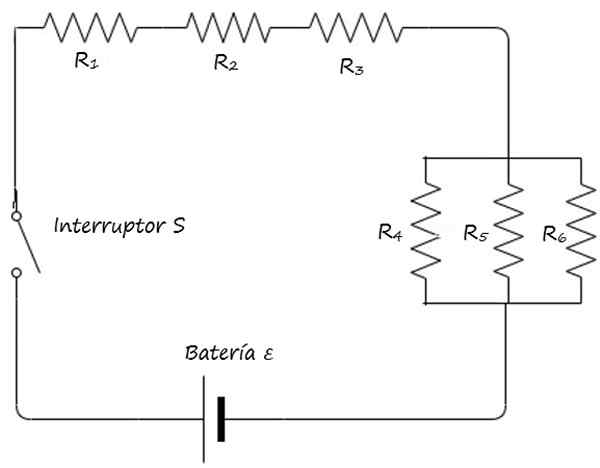
Piirrä aloituskuvion sekoitettu piiri, käyttämällä yllä kuvattuja symboleja.

Vastaus

Esimerkki 2

Esimerkin 1 piirissä sinulla on seuraavat vastus- ja akun arvot:

R -₁ = 50 Ω; R -₂ = 100 Ω; R -₃ = 75 Ω, R₄ = 24 Ω, R₅ = 48 Ω; R -₆ = 48 Ω; ε = 100 V

Näytetyn piirin suhteen akkua pidetään ihanteellisena, ts. Sillä ei ole sisäistä vastustusta. Yleensä todellisilla paristoilla on pieni sisäinen vastus, joka on piirretty sarjaan akun kanssa ja niitä käsitellään samalla tavalla kuin muut piirin vastukset.

Laske seuraava:

• a) piirin vastaava vastus.
• b) Akusta tulevan virran arvo.
• c) Jännitteet ja virrat jokaisessa resistanssissa.

Vastaa

Ensimmäinen vastusryhmä: R₁ = 50 Ω; R -₂ = 100 Ω; R -₃ = 75 Ω on kytketty sarjaan, joten vastaava vastus on R₁₂₃-

R -₁₂₃ = R₁ + R -₂ + R -₃ = 50 ω + 100 ω + 75 ω = 225 Ω

Se voi palvella: Kolmas termodynamiikan laki: kaavat, yhtälöt, esimerkit

R -vastusryhmän suhteen₄ = 24 Ω, R₅ = 48 Ω; R -₆ = 48 Ω, on kytketty rinnakkain ja vastaava kaava on käytettävä:

 Edellisen tuloksen vastavuoroinen tai käänteinen on ryhmän vastaava vastus:

R -₄₅₆ = 12 Ω

Saatu yksinkertaistettu piiri on esitetty seuraavassa kaaviossa, joka koostuu kahdesta sarjan vastustamisesta akun tai akun kanssa. Nämä kaksi vastustusta lisätään alkuperäisen R -piirin vastaavan vastuskyvyn löytämiseksi_Eq-

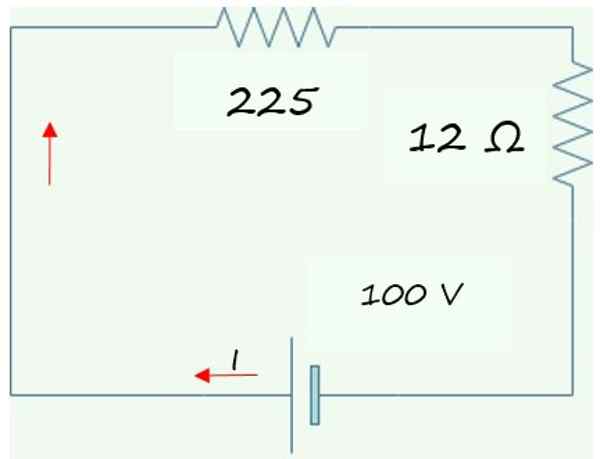
R -_Eq= 225 Ω + 12 ω = 237 Ω

Vastaus b

Akun poistuva virta (konventin mukaan aina positiivinen napa piirtää aina yksinkertaistetulla piirillä, joka koostuu vastaavasta vastus R: stä_Eq Sarjassa akun kanssa, johon OHM: n lakia sovelletaan:

ε = i · r

I = ε / r = 100 V / 237 ω = 0.422 a

Vastaus C

Jännitteet ja virrat jokaisessa SA -vastustuskysymyksessä lasketaan Ohmin lain mukaan. Ensimmäinen asia, joka havaitaan₁ , R -₂ ja r₃ Ja sen sijaan se on jaettu ylittämällä r₄ , R -₅ ja r₆.

Jännitteet v₁, V₂ ja v₃ ovat:

V₁  = 0.422 a × 50 ω = 21.1 V
V₂  = 0.422 a × 100 ω = 42.2 V
V₃  = 0.422 a × 75 ω = 31.7 V

Puolestaan ​​Voltajes V₄, V₅ ja v₆ Niillä on sama arvo, koska resistanssit ovat rinnakkain:

V₄ = V₅ = V₆ = 0.422 a × 12 ω = 5.06 V

Ja vastaavat virrat ovat:

Yllyttää₄ = 5.06 V / 24 ω = 0.211 a

Yllyttää₅ = I₆ = 5.06 V / 48 ω = 0.105 a

Huomaa, että lisäämällä I₄, Yllyttää₅ ja minä₆ Akun kokonaisvirta saadaan uudelleen.