Kiinteät aineet, nesteet, kaasut, esimerkit

Se puristuvuus aine tai materiaali on tilavuuden muutos, jonka se kokee, kun se on paineenvaihto. Yleensä tilavuus pienenee, kun levitetään painetta järjestelmään tai objektiin. Toisinaan tapahtuu kuitenkin päinvastoin: paineen muutos voi tuottaa räjähdyksen, jossa järjestelmä lisää tilavuutta tai kun vaihemuutos tapahtuu.

Joissakin kemiallisissa reaktioissa tämä voi tapahtua ja myös kaasuissa, koska lisäämällä törmäysten tiheyttä, torjuntavoimat tapahtuvat.

Sukellusvene kokee puristusvoimia upotettuna. Lähde: Pixabay.com.

Kuvittelemalla, kuinka helppoa tai vaikeaa voi olla objektin puristaminen, sinun on otettava huomioon kolme tilaa, joissa asia on normaalisti: kiinteä, nestemäinen ja kaasumainen. Jokaisessa heistä molekyylit pitävät tiettyjä etäisyyksiä toisistaan. Mitä entistä enemmän linkkejä, jotka yhdistävät esineen ja lähemmäksi muodostuvat ainemolekyylit, sitä vaikeampaa on muodonmuutoksen aiheuttaminen.

Kiinteällä on erittäin läheiset molekyylit, ja yrittäessään enemmän, torjuntavoimat ilmestyvät, jotka estävät tehtävää. Siksi sanotaan, että kiinteät aineet ovat kompensoivia. Nestemäisissä molekyyleissä on enemmän tilaa, joten sen puristuvuus on suurempi, mutta silti tilavuuden muutos vaatii yleensä suuria voimia.

Joten kiinteät aineet ja nesteet ovat tuskin puristuvia. Erittäin suuri painevaihtelu olisi tarpeen saavuttaakseen huomattava muutos So -nimellä normaalissa paine- ja lämpötila -olosuhteissa. Toisaalta kaasut, koska niillä on erittäin etäisyydellä sijaitsevat molekyylit, puristetaan helposti ja purkautuvat.

[TOC]

Vankka puristuvuus

Kun esine upotetaan esimerkiksi nesteeseen, se painostaa esinettä kaikkiin suuntiin. Tällä tavoin voimme ajatella, että esineen tilavuus vähenee, vaikka useimmissa tapauksissa tämä ei ole huomattavaa.

Tilanne näkyy seuraavassa kuvassa:

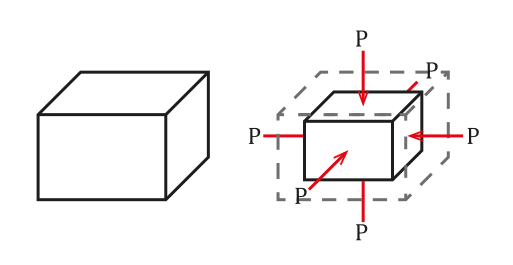Upotetun esineen nesteen aiheuttama voima on kohtisuorassa pintaan nähden. Lähde: Wikimedia Commons.

Paine määritellään voimana pinta -alayksikköä kohti, mikä aiheuttaa tilavuudenmuutoksen ΔV verrannollinen objektin V alkuperäiseen tilavuuteen_jompikumpi. Tämä volyymin muutos riippuu saman ominaisuuksista.

Hooken laissa todetaan, että esineen kokemat muodonmuutokset ovat verrannollinen siihen sovellettaviin ponnisteluihin:

Ponnistelu ∝ muodonmuutos

Kehon kokemat tilavuusmuodot määritetään b: llä vaadittu suhteellisuusvakio, jota kutsutaan nimellä materiaalin tilavuusmoduuli-

B = -seft/yhtenäinen muodonmuutos

Voi palvella sinua: Lämpösäteily: Ominaisuudet, esimerkit, sovellukset

B = -Ap/ (ΔV/ V_jompikumpi-A

Kuten Δv/v_jompikumpi Se on mitaton määrä, koska se on kahden määrän välinen osoitus, tilavuusmoduulilla on samat paineyksiköt, jotka kansainvälisessä järjestelmässä ovat Pascal (PA).

Negatiivinen merkki osoittaa tilavuuden odotetun vähentymisen, kun objekti on riittävästi, ts. Paine kasvaa.

-Materiaalin puristus

Tilavuusmoduulin käänteinen tai vastavuoroinen arvo tunnetaan nimellä puristuvuus Ja se on merkitty sanoituksilla k -k -. Siksi:

Tässä k -k - Se on negatiivinen fraktiotilavuuden muutoksesta, joka johtuu paineen noususta. Sen yksiköt kansainvälisessä järjestelmässä ovat PA: n käänteinen² /N.

B -tai k: n yhtälöä voidaan soveltaa sekä kiinteisiin aineisiin että nesteisiin. Volumetrisen moduulikonseptia sovelletaan harvoin kaasuihin. Myöhemmin yksinkertainen malli selitetään määrän määrän määrän määrittämiseksi, jonka todellinen kaasu voi kokea.

Äänen nopeus ja puristusmoduuli

Mielenkiintoinen sovellus on äänen nopeus väliaineessa, joka riippuu saman puristusmoduulista:

Missä C on äänen nopeus, B on tilavuusmoduuli ja ρ on väliaineen tiheys

Ratkaisut harjoitukset-esimerkkejä

-Liikunta ratkaistiin 1

Kiinteä messinkipallo, jonka tilavuus on 0.8 m³ Se putoaa valtamereen syvyyteen, jossa hydrostaattinen paine on 20 m suurempi kuin pinnalla. Mikä muutos kokee pallon määrän? Tiedetään, että messinki puristusmoduuli on B - = 35 000 MPa,

Ratkaisu

1 m pa = 1 mega pascal = 1. 10 ⁶ Paa

Painevaihtelu pintaan on dp = 20 x 10 ⁶ Paa. Sinulla on annettu yhtälö B: lle, sinulla on:

B = -Ap/ (ΔV/ V_jompikumpi-A

Siksi:

Niin:

Δv = -5.71.10 ^-4 x 0.8 m³ = -4.57 x 10^-4 m³

Tilavuuserolla voi olla negatiivinen merkki, kun lopullinen tilavuus on pienempi kuin alkuperäinen tilavuus, joten tämä tulos sopii kaikkiin tähän mennessä tekemiin oletuksiin.

Puristusmoduuli niin korkea, osoittaa, että paineessa vaaditaan suuri muutos siten, että objekti kokee huomattavan äänenvoimakkuuden vähenemisen.

-Liikunta ratkaistiin 2

Korvan asettaminen junaraiteille tiedetään, kun yksi näistä ajoneuvoista lähestyy etäisyyttä. Kuinka kauan ääni kestää, kun matkustat teräskiskon läpi, jos juna on 1 km päässä?

Voi palvella sinua: lineaarisen vauhdin säilyttäminen: periaate, esimerkit, harjoitukset.

Tiedot

Terästiheys = 7.8 x 10 ³ kg/m3

Teräspuristusmoduuli = 2.0 x 10 ^yksitoista Paa.

Ratkaisu

Nesteiden puristuvuus

Yllä laskettu puristusmoduuli B sovelletaan myös nesteisiin, vaikka yleensä tarvitaan suurta vaivaa, jotta volyymi vähenee huomattavasti. Mutta nesteet voivat laajentua tai supistuessaan, kun ne lämmitävät tai jäähtyvät, ja myös jos niitä lannistuu tai paineistetaan.

Vesien vakiopaine- ja lämpötila -olosuhteissa (0 ºC ja noin 100 kPa paine -ilmakehän) tilavuusmoduuli on 2100 MPa. Eli noin 21000 -kertainen ilmakehän paine.

Siksi useimmissa sovelluksissa nesteitä pidetään yleensä puristamattomina. Tämä näkyy heti numeerisella sovelluksella.

-Liikunta ratkaistiin 3

Löydä veden tilavuuden murto -osan väheneminen, kun se on painettu 15 MPa.

Ratkaisu

Kaasujen puristus

Kaasut, kuten edellä selitetään, toimivat hiukan eri tavalla.

Tietää, mikä tilavuus heillä on n tietyn kaasun moolit, kun sitä pidetään rajoitettuna paineessa P ja lämpötilassa T, Osavaltion yhtälöä käytetään. Ihanteellisen kaasun tilayhtälössä, jossa molekyylien välisiä voimia ei oteta huomioon, yksinkertaisin malli osoittaa, että:

P.V_{ihanteellinen} = n. R -. T

Missä r on ihanteellisten kaasujen vakio.

Kaasun tilavuuden muutokset voidaan suorittaa vakiopaineessa tai vakiona lämpötilassa. Esimerkiksi pitämällä lämpötilavakio, isoterminen puristuvuus κ_T On:

Ennen kiinteiden aineiden käsitteen määrittelemistä käytetyn ”delta” -symbolin sijasta se on kuvattu johdannaisella, tässä tapauksessa osittain johdettu P: n suhteen, ylläpitämällä vakio t t.

Siksi B -_T Isoterminen puristusmoduuli on:

 B -_T = p

Ja myös adiabaattinen bu -puristusmoduuli B on tärkeä_{adiabaattinen}, Jolle ei ole tulevaa tai lähtevää lämpövirtausta.

B -_{adiabaattinen} = γp

Missä γ on adiabaattinen kerroin. Tällä kertoimella voit laskea äänen nopeuden ilmassa:

-Liikunta ratkaistiin 4

Edellisen yhtälön soveltamalla äänen nopeus ilmassa.

Tiedot

Adiabaattinen ilman puristusmoduuli on 1,42 × 10⁵ Paa

Ilmatiheys on 1.225 kg/m³ (Ilmakehän paineella ja 15 ºC)

Ratkaisu

Puristuskerroin z

Sen sijaan, että työskentelisit puristusmoduulin kanssa, paineenvaihdon johtuen yksikön tilavuuden muutoksena todellinen kaasun puristuskerroin, Erilainen, mutta havainnollistava käsite siitä, kuinka todellinen kaasu verrataan ihanteelliseen kaasuun:

Voi palvella sinua: Valon aaltoileva teoria: Selitys, sovellukset, esimerkit

P . V_todellinen = Z. R -. T

Jos z on kaasun puristuvuuden johdettavuus, joka riippuu olosuhteista, joissa se on, on yleensä sekä P- että lämpötilan T -paineen funktio, kykenemällä ilmaisemaan itsensä seuraavasti:

Z = f (p, t)

Ihanteellisen kaasun z = 1 tapauksessa. Oikeiden kaasujen z -arvo kasvaa melkein aina paineen kanssa ja laskee lämpötilan kanssa.

Kasvaamalla painetta kaasumaiset molekyylit törmäävät useammin ja niiden väliset torjuvat voimat lisääntyvät. Tämä voi johtaa todellisen kaasun määrän lisääntymiseen, joten z> 1.

Toisaalta paineen alentamiseksi molekyylit voivat vapaasti liikkua ja vetovoiman voimat ovat vallitsevia. Tässä tapauksessa z < 1.

Yksinkertaisen tapauksen 1 mol kaasua n = 1, jos sama paine- ja lämpötilaolosuhteet ylläpidetään, jakamalla termi aiemmat yhtälöt saadaan:

On päätelty, että:

V_todellinen = Z v_{ihanteellinen}

-Liikunta ratkaistiin 5

Paineessa on todellinen kaasu 250 ºK ja 15 atm, jonka tilavuus 12 % on alhaisempi kuin ihanteellisten kaasujen tilalla laskettu. Jos paine ja lämpötila pysyvät vakiona, etsi:

a) puristuskerroin.

b) todellisen kaasun molaarinen tilavuus.

c) Millaiset voimat ovat vallitsevia: houkutteleva tai torjuttava?

Ratkaisu

a) Jos todellinen tilavuus on 12 % pienempi kuin ihanne, se tarkoittaa:

V_todellinen = 0.88 V_{ihanteellinen}

Siksi 1 mol kaasua, puristuskerroin on:

Z = 0.88

b) Ideaalikaasujen vakion valitseminen asianmukaisilla yksiköillä annettuihin tietoihin:

R = 0,082 l.atm/mol.K -k -

Molaarinen tilavuus lasketaan tyhjentämällä ja korvaamalla arvot:

c) houkuttelevat voimat ovat vallitsevia, koska z on alle 1.

Viitteet

1. Atkins, p. 2008. Fysikaalinen kemia. Pan -american lääketieteellinen toimitus. 10 - 15.
2. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. 6^th. Ed Prentice Hall. 242 - 243 ja 314-15
3. Mott, r.  2006. Fluidimekaniikka. Pearson -koulutus.13-14.
4. Rex, a. 2011. Fysiikan perusteet. Pearson -koulutus. 242-243.
5. Tipler, P. (2006) Tieteen ja tekniikan fysiikka. 5. ed. Osa 1. Toimitus palautti. 542.