Suhteellisuusvakio mikä on, laskenta, harjoitukset

Se suhteellisuusvakio Se on relaatio numeerinen elementti, jota käytetään samankaltaisuuskuvion määrittelemiseen 2 suuruuten välillä, jotka ovat samanaikaisesti muutettuja. On hyvin yleistä edustaa sitä yleisenä lineaarisena funktiona ekspression f (x) = k kautta.X. Tämä ei kuitenkaan ole ainoa mahdollisen suhteellisuuden esitys.

Esimerkiksi X: n ja Y: n välisellä suhteella Y = 3x -funktiossa on vakio suhteellisuus, joka on yhtä suuri kuin 3. Se osoittaa, että kun riippumaton muuttuja X kasvaa, niin myös riippuvainen muuttuja ja sen edellisen arvon kolminkertainen.

Yhdessä muuttujassa sovelletuilla muutoksilla on välittömät vaikutukset toisaalta, niin että on olemassa arvo, jota kutsutaan vakiona suhteellisuudesta. Tämän tarkoituksena on yhdistää erilaiset suuruudet, jotka molemmat muuttujat hankkivat.

[TOC]

Mikä on suhteellisuuden ja tyyppien vakio

Muuttujien muuttamisen suuntauksen mukaan suhteellisuudet voidaan luokitella kahteen tyyppiin.

Suora suhteellisuus

Ehdottaa kahden suuruuden välistä yksisuuntaista suhdetta. Siinä, jos riippumaton muuttuja aiheuttaa jonkin verran kasvua, myös riippuvainen muuttuja kasvaa. Samoin riippumattoman muuttujan väheneminen aiheuttaa vähentyneen ja.

Esimerkiksi johdannossa käytetty lineaarinen funktio; Y = 3x, vastaa suoraa suhteellisuussuhdetta. Tämä johtuu siitä, että riippumattoman muuttujan X kasvu aiheuttaa kolminkertaisen lisääntymisen riippuvaisen muuttujan edellisessä arvossa ja.

Samoin riippuvainen muuttuja vähentää kolminkertaista arvonsa, kun x laskeutuu suuruuteen.

Suhteellisuusvakion "k" arvo suorassa suhteessa määritellään k = y/x.

Käänteinen tai epäsuora suhteellisuus

Tämän tyyppisissä funktioissa muuttujien välinen suhde esitetään antonymin, jossa riippumattoman muuttujan kasvu tai lasku vastaa vastaavasti riippuvaisen muuttujan laskua tai kasvua.

Se voi palvella sinua: Luonnollisten lukujen hajoaminen (esimerkit ja harjoitukset)

Esimerkiksi funktio f (x) = k/x on käänteinen tai epäsuora suhde. Koska riippumattoman muuttujan arvo alkaa kasvaa, K: n arvo jaetaan kasvavalla lukulla, mikä tekee riippuvaisesta muuttujan arvon vähenemisestä osuuden mukaan.

K: n ottaman arvon mukaan suhteellisen käänteisen toiminnan taipumus voidaan määritellä. Jos k> 0, niin funktio pienenee kaikissa reaalilukuissa. Ja sen kuvaaja sijaitsee 1. ja 3. kvadrantissa.

Päinvastoin, jos K: n arvo on negatiivinen tai pienempi kuin nolla, funktio kasvaa ja sen kuvaaja löytyy 2. ja 4 -kvadrantista.

Kuinka se lasketaan?

On olemassa erilaisia ​​tilanteita, joissa suhteellisuusvakion määritelmä voidaan tarvita. Eri tapauksissa esitetään erilaisia ​​tietoja ongelmasta, missä näiden tutkimus osoittaa lopulta K: n arvon.

Yleisellä tavalla edellä mainittu voidaan koota uudelleen. K: n arvot vastaavat kahta lauseketta läsnä olevan suhteellisuuden tyypin mukaan:

- Suora: k = y/x

- Käänteinen tai epäsuora: k = y.X

Kaaviosi mukaan

Joskus vain funktion kaavio tunnetaan osittain tai kokonaan. Näissä tapauksissa se on tarpeen graafisella analyysillä määritettävä suhteellisuustyyppi. Sitten meidän on määritettävä koordinaatti, jonka avulla X: n ja Y: n arvot voidaan tarkistaa vastaavaan K -kaavaan.

Suoraan suhteellisuuteen viittaavat kaaviot ovat lineaarisia. Toisaalta käänteisten suhteellisten funktioiden kaaviot muuttuvat yleensä hyperboleista.

Arvotaulukon mukaan

Joissakin tapauksissa on arvotaulukko, jonka arvot vastaavat riippumattoman muuttujan kutakin iteraatiota. Normaalisti tämä merkitsee kaavion toteutumista K: n arvon määrittelemisen lisäksi.

Voi palvella sinua: Taajuuden jakautuminen: Kuinka tehdä taulukko, esimerkki, liikunta

Analyyttisen ilmaisun mukaan

Näyttää lausekkeen, joka määrittelee analyyttisesti. Suoraan k: n arvo voi olla selvä, tai se voidaan myös päätellä itse lausekkeesta.

Kolmen suoran tai yhdisteen säännönä

Muissa harjoitusmalleissa on tiettyjä tietoja, jotka viittaavat arvojen väliseen suhteeseen. Tämä tekee tarvittavan kolmen suoran tai yhdisteen soveltamisen muiden tarvittavien tietojen määrittelemiseksi vuodessa.

Historia

Suhteellisuuden käsite on aina ollut läsnä. Ei vain suurten matemaatikkojen mielessä ja työssä, vaan myös väestön jokapäiväisessä elämässä heidän käytännöllisyyden ja sovellettavuuden vuoksi.

On hyvin yleistä täyttää tilanteet, jotka vaativat suhteellisuuslähestymistapaa. Nämä esitetään kussakin tapauksessa, joissa verrataan muuttujia ja ilmiöitä, jotka pitävät tiettyjä suhteita.

Aikajanan kautta voimme luonnehtia historiallisia hetkiä, jolloin suhteellisuutta koskevat matemaattiset edistykset on sovellettu.

- Toinen vuosisata a.c. Kreikan jaostojen varastointijärjestelmä otetaan käyttöön.

- 5. vuosisata a.c. Kreikassa löydetään myös osuus, joka liittyy neliön sivuun ja diagonaaliin.

- 600 a.c. Tales de Mileto esittelee lauseensa suhteellisuudesta.

- Vuosi 900. Intian aikaisemmin käyttämää desimaalijärjestelmää syistä ja mittasuhteista laajennetaan. Arabien panos.

- Xvii Century. Osallistukset viittaavat Eulerin laskennan mittasuhteisiin.

- XIX -vuosisata. Gauss tarjoaa kompleksiluku- ja osuuksien käsitteen.

- Kahdeskymmenes vuosisata. Suhteellisuus funktiomallina määrittelee sokeri ja deulofeo.

Ratkaisut

Harjoitus 1

Sen on laskettava muuttujien arvo x, y, z ja g. Seuraavien suhteiden tunteminen:

3x + 2y - 6z + 8g = 1925

Voi palvella sinua: jatkuva satunnaismuuttuja

x/3 = y/8 = z/3 = g/5

Suhteellisuusvakion suhteelliset arvot määritetään. Ne voidaan saada toisesta suhteesta, jossa kukin muuttujan jakaminen arvo osoittaa suhteen tai syyn K: n suhteen.

X = 3K y = 2K z = 3K g = 5K

Arvot korvataan ensimmäisessä lausekkeessa, jossa uusi järjestelmä arvioidaan yhtenä K -muuttujana.

3 (3K) + 2 (2K) - 6 (3K) + 8 (5K) = 1925

9K + 4K -18K + 40K = 1925

35K = 1925

K = 1925/35 = 55

Tätä suhteellisuusvakion arvoa käyttämällä löydämme kuvan, joka määrittelee jokaisen muuttujan.

x = 3 (55) = 165 y = 2 (55) = 110

Z = 3 (55) = 165 g = 5 (55) = 275

Harjoitus 2

Laske suhteellisuusvakio ja funktion määrittelevä lauseke, kun otetaan huomioon sen grafiikka.

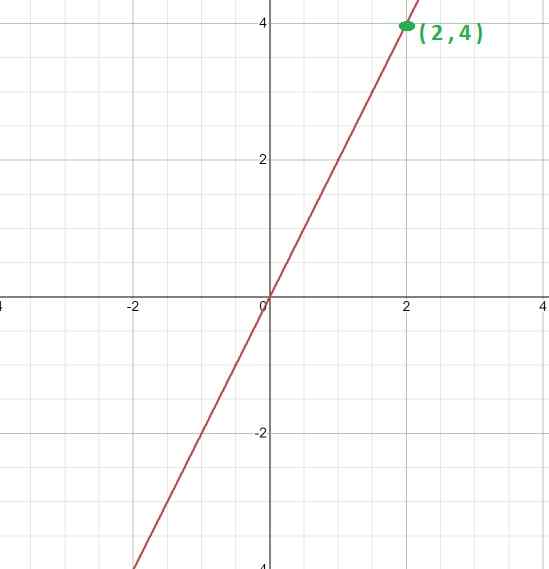
Ensinnäkin kaavio analysoidaan, sen lineaarinen merkki on ilmeinen. Tämä osoittaa, että se on funktio, jolla on suora suhteellisuus ja että K: n arvo saadaan lausekkeen k = y/x kautta

Sitten valitaan kaavion määritettävissä oleva kohta, ts. Se, jossa sen muodostavat koordinaatit voivat olla tarkkoja.

Tätä tapausta kohta otetaan (2, 4). Missä voimme luoda seuraavan suhteen.

K = 4/2 = 2

Niin, että lauseke määritetään y = kx -funktiolla, joka tässä tapauksessa on

F (x) = 2x

Viitteet

1. Sähkö- ja elektroniikan matematiikka. DR. Arthur Kramer. Cengage Learning, 27. heinäkuuta. 2012
2. Vision 2020: Operatiivisen tutkimuksen strateginen rooli. N. Ravichandran. Liittolaisten kustantajat, 11. syyskuuta. 2005
3. GRAMMATICAL ja aritmeettinen tieto valtion hallinnollisesta avustajasta.e-kirja. Hullu
4. Matematiikan vahvistus opetussuunnitelman tukemiseksi ja monipuolistamiselle: Opetussuunnitelman tuen ja monipuolistamisen kannalta. Mª Lourdes Lázaro Soto. Narcea Ediciones, 29. elokuuta. 2003
5. Logistiikka ja kaupallinen hallinta. Maria José Escudero Serrano. Paraninfo Editions, S.-Lla., 1. syyskuuta. 2013