Nopeusvakio

Mikä on nopeusvakio?

Se nopeusvakio Kemiallisen kinetiikan nopeuslain suhteellisuus on vakio, joka luo suhteet reagenssien molaarisen pitoisuuden ja reaktion nopeuden välillä.

Reagenssina reaktionopeudet kuluttavat myös. Siksi nopeusvakion laskelmissa, joita edustavat 'k' -symboli, alkuperäiset nopeudet otetaan huomioon, jotta vertailupiste on useiden kokeiden välillä.

Kemiallinen kinetiikka osoittaa, että tämä vakio riippuu reagenssien reaktiojärjestyksistä, joiden pitoisuudet muuttavat reaktion nopeutta.  Toisaalta Arrhenius -yhtälön mukaan K riippuu myös reaktion lämpötila- ja aktivointienergiasta.

Siksi sanotaan, että nopeusvakio ei ole todellinen vakio, koska se vaihtelee lämpötilan mukaan ja myös aktivointienergiaa muuttavien katalyytit, jotka. Siksi ei ole monia taulukoita, joissa ne tulevat tiettyihin reaktioihin (ja olosuhteisiin).

Esimerkiksi reaktiossa, jossa a ja b reagoivat, jokaisella on 1 reaktiojärjestys, vakio ilmoitti K: stä 25 ° C: seen ja lisäämällä tietyn määrän katalyyttiä, se ei ole sama, jos reaktio tehdään lämpötilaan 26 tai 27 ºC. Pienin variaatio vaikuttaa K: n arvoon, joka on vakio vain kokeisiin perustettujen olosuhteiden aikana.

Kuinka laskea nopeusvakio?

Kokeilu

Reaktion nopeusvakion arvon määrittäminen tehdään kokeellisesti. Jos haluat esimerkiksi määrittää nopeusvakion arvon muodon reaktiolle:

A +B → C

K: n arvon määrittämiseksi voidaan tehdä kolme reaktiota seuraavilla eroilla: reaktiossa 2 reagenssin A alkuperäinen konsentraatio on vakio, [A], mutta se kaksinkertaistuu, esimerkiksi reagenssin B konsentraatio, [ B].

Samaan aikaan reaktiossa 3 [A] kaksinkertaistuu reaktioon 1 verrattuna, pitäen vakiona [b].

Siten rakennetaan pitoisuustaulukko, joka verrataan alkuperäisiä nopeuksia useiden kokeiden välillä. Tämä tarkoituksena määrittää reaktiomääräykset ja peräkkäin nopeusvakion laskemiseksi.

Voi palvella sinua: Alumiinihydroksidi: rakenne, ominaisuudet, käytöt, riskit

Reaktiomääräykset

Ensimmäinen laskenta

Edellisessä reaktiossa sen nopeus ilmaistaan ​​yhtälöllä:

Reaktionopeus = K · [A]^x· [B]^ja

Missä 'x' e 'ja' vastaavat reagenssien a ja b reaktiomääräyksiä, vastaavasti.

Reaktiojärjestysten arvojen määrittämiseksi on tehtävä vertailu reaktion 2 ja 1 välillä, samoin kuin reaktion 3 ja 1 välillä.

Kun verrataan reaktiota 1 2: iin, voidaan havaita esimerkiksi, että kopioimalla [B] reaktionopeuden päällekkäisyys.

Sitten: [B]: n osuus reaktioiden 2 ja 1 välillä on 2, samoin kuin reaktioiden nopeuksien välinen osuus. Sitten reaktion järjestysarvo voidaan saada suhteessa B: hen (eksponentti ja) seuraavan lähestymistavan kautta:

Reaktion luokan "ja" laskeminen. Lähde: Gabriel Bolívar.

Kokeen 2 nopeus on kahdesti nopeampi kuin kokeen nopeus 1. Siten jakamalla kaksi yllä olevaa yhtälöä, meillä on:

2 = 2^ja

Siksi 'ja' Vale 1, kyky päätellä, että reagenssin B: n suhteen on ensimmäisen asteen järjestys.

Toinen laskenta

Samalla tavalla jatkamme reagenssin A laskemista 'x':

Reaktion luokan "x" laskeminen. Lähde: Gabriel Bolívar.

Kokeen tai reaktion nopeus 3 on neljä kertaa korkeampi kuin koe tai reaktio 1. Siksi:

4 = 2^x

JOMPIKUMPI

2² = 2^x

Ja x: n arvo on 2, joten reaktio on toinen järjestys suhteessa reagenssiin.

Lopullinen raivaus

Sitten voidaan määrittää nopeusvakion arvo, joka perustuu mihin tahansa reaktioon:

Reaktionopeus = K · [A]²· [B]

Tarpeeksi ottamaan käyttöön kokeellisia arvoja ja selkeää k: n:

K = Reaktionopeus / ([A]²· [B])

Esimerkit

Seuraavat esimerkit toimivat johdannona ennen kuin harjoitukset ratkaistiin seuraavasta osasta.

Esimerkki 1

Kemiallisessa reaktiossa:

a) Jos reagenssin alkuperäinen pitoisuus kaksinkertaistaa reaktion nopeuden: mikä on reaktion järjestys tämän reagenssin suhteen?

b) Jos reagenssipitoisuuden lisääntyminen aiheuttaa nopeuden lisääntymistä kertoimessa 8, mikä olisi reaktion järjestys?

c) Jos reagenssin pitoisuus kokee muutoksen ja nopeus pysyy samana: mikä on reaktion järjestys reagenssin suhteen?

Se voi palvella sinua: sykopropaani (C3H6)

A) reaktionopeuden osuus on sama ja reagenssipitoisuuksien osuus on yhtä kuin 2^x,

2 = 2^x

Siksi x = 1 ja reaktion rikos suhteessa reagenssiin on 1.

B) reaktionopeuden osuus on sama 8 (2³) ja reagenssipitoisuuksien osuus on yhtä suuri kuin 2^x,

2³ = 2^x

Siksi x = 3 ja reaktion järjestys suhteessa reagenssiin on 3-

Kun taas c) reaktion nopeus on riippumaton reagenssin pitoisuudesta, niin reagenssin suhteen reagenssin järjestys on nolla.

Esimerkki 2

Reaktio:

2 Ei₂  +  JOMPIKUMPI₂ → 2 Ei₂

Sillä on seuraavan nopeuslain ilmaisu:

Reaktionopeus = k · [ei₂-²·JOMPIKUMPI₂.

Mikä on reaktion globaali järjestys? Mitä yksiköitä k on?

Reaktion järjestys tai₂ Se on 1, ja reaktion järjestys suhteessa ei₂ Se on 2, joten reaktion globaali järjestys on näiden arvojen summa, ts. 2 + 1 = 3.

Reaktion nopeudella on M/S -yksiköt, ja reagenssien pitoisuudet ilmaistaan ​​M: ssä. Analyysi yksiköistä, joita meillä on:

k = reaktionopeus / ([ei₂-²·[JOMPIKUMPI₂-

= (M / s) / (m³-A

= s^-1M^-2

Ratkaisut

Harjoitus 1

Seuraavan reaktion tiedot saatiin 25 ° C: ssa:

A +2 B → C +2 D

Mikä on tämän reaktion nopeuslain ilmaus? Mikä on nopeusvakion arvo?

Reaktiomääräysten laskelmat

Kokeelliset tiedot ovat:

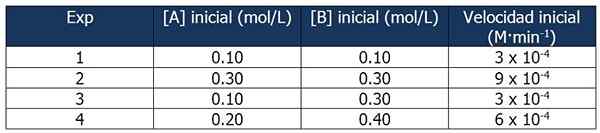Suoritusta harjoituksista 1. Lähde: Gabriel Bolívar.

Kokeiden 1 ja 3 vertailu antaa sinun tehdä seuraavat johtopäätökset:

Reaktioiden 3 ja 1 nopeuden välinen osuus:

3 x 10^-4 M · min^-1 / 3 x 10^-4 M · min^-1 = 1

Mutta B -pitoisuuksien välinen osuus on:

(0.3 mol / l) / (0.1 mol/l) = 3

Reaktion nopeus on riippumaton B: n pitoisuudesta, koska sen kasvu ei vaikuta siihen. Siksi reaktion R -järjestys reagenssiin B: n suhteen on nolla.

Toisaalta reaktioiden 4 ja 1 vertailu sallii seuraavat johtopäätökset:

6 x 10^-4 M · min^-1 / 3 x 10^-4 M · min^-1 = 2

Samaan aikaan reaktioiden 4 ja 1 [A] välinen osuus on yhtä suuri kuin:

Voi palvella sinua: 5 homogeenisten seosten ominaisuuksia

(0.20 mol / l) / (0.10 mol/l) = 2^x

Silloin suhteiden välinen suhde on:

2 = 2^x

x = 1

Siksi nopeuslain ilmaisu on:

Reaktionopeus = K · [A]

B: tä ei oteta sisään, koska sen reaktion järjestys on nolla.

K -laskenta

Voimme laskea nopeusvakion mistä tahansa kineettisestä tiedosta. Käytetään kokeilu 1:

K = Reaktionopeus / [A]

= 3 x 10^-4 M · min^-1 / 0.10 m

= 3 x 10^-3 tai 0.003 min^-1

Harjoitus 2

Reaktionopeuden tiedot saatiin tietyssä lämpötilassa.

2 CLO₂ (AC) +2 OH^- (AC) → CLO₃^- (AC) +CLO₂ (AC) +H₂Tai (l)

Reaktiomääräysten laskelmat

Kokeelliset tiedot ovat:

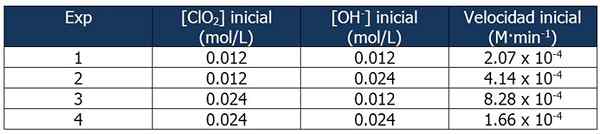KESKUSTUS TARJOAMINEN 2. Lähde: Gabriel Bolívar.

Reaktion 2 ja reaktion 1 nopeuden välinen osuus on:

4.14 x 10^-4 M · min^-1 / 2.07 x 10^-4 M · min^-1 = 2

Ja OH -pitoisuuksien osuus^- Reaktioiden 2 ja 1 välillä on yhtä suuri kuin:

(0,024 mol/l)/(0,012 mol/l) = 2^x

Eksponentti 'x' edustaa reaktion järjestystä suhteessa OH -reagenssiin^-. Laskettujen mittasuhteiden välinen suhde voidaan esittää seuraavasti:

2 = 2^x

x = 1

Siksi reaktion järjestys suhteessa OH -reagenssiin^- on yhtä suuri kuin 1.

Reaktiossa 3 CLO: n pitoisuus kaksinkertaistuu₂ reaktio 1, kun taas OH: n pitoisuus^- Pysyy vakiona.

Reaktioiden 3 ja 1 nopeuden välinen osuus:

(8.28 x 10^-4 M · min^-1) / (2.07 x 10^-4 M · min^-1) = 4 (2²-A

Ja [CLO: n osuus₂] reaktioiden 3 ja 1 välillä on yhtä suuri kuin:

(0,024 mol/l)/(0,012 mol/l) = 2^ja

Eksponentti 'ja' edustaa CLO -reagenssin reaktion järjestystä₂.

Vertailu mittasuhteita:

2² = 2^ja

4 = 2^ja

y = 2

Siksi reaktio on toinen CLO -reagenssin suhteen₂.

Nopeuslain ilmaisu tulee sitten:

Reaktionopeus = k · [CLO₂-²· [Vai niin^--

K -laskenta

Jälleen voimme laskea k: n edellisestä lausekkeesta käyttämällä mitä tahansa kokeiden kineettistä tietoa. Käytämme kokeilua 3:

K = (8.28 x 10^-4 M · min^-1) / (0.024 m)² (0.012 m)

= 119.79 min^-1· M^-2

Viitteet

1. Whitten, Davis, Peck & Stanley. (2008). Kemia. (8. ed.-A. Cengage -oppiminen.
2. Wikipedia. (2020). Reaktionopeusvakio. Haettu: vuonna.Wikipedia.org
3. Kemia Texas A&M University. (S.F.-A. Kinetiikka: näytteenottoasteen laskelmat. Palautettu: Chem.tamu.Edu
4. Keith J. Lakkaus. (2020). Reaktionopeus. Britannica Encyclopaedia. Toipunut: Britannica.com
5. Helmestine, Anne Marie, PH.D -d. (25. elokuuta 2020). Mikä on nopeusvakio kemiassa? Toipunut: Admingco.com
6. Clark Jim. (2013). Nopeusvakiot ja Arrhenius -yhtälö. Talteenotettu: Chemguide.yhteistyö.Yhdistynyt kuningaskunta