Kuinka monta ratkaisua neliömäisellä yhtälöllä on?

Neliöyhtälöllä tai toisen asteen yhtälöllä voi olla nolla, yksi tai kaksi todellista ratkaisua, riippuen mainitussa yhtälössä näkyvistä kertoimista. Jos työskentelet monimutkaisten numeroiden kanssa, voit sanoa, että jokaisessa neliömäisessä yhtälössä on kaksi ratkaisua.

Neliömäisen yhtälön aloittamiseksi se on ax²+bx+c = 0 -muodon yhtälö, jossa a, b ja c ovat todellisia lukuja ja x on muuttuja.

Sanotaan.

Jos sinulla on esimerkiksi yhtälö x²-4x+4 = 0, niin x1 = 2 on ratkaisu, koska (2) ² (2) +4 = 4-8+4 = 0.

Päinvastoin, jos x2 = 0 korvataan, se saadaan (0) ²-4 (0) +4 = 4 ja AS 4 ≠ 0, niin x2 = 0 ei ole neliömäisen yhtälön ratkaisu.

Neliöyhtälön ratkaisut

Neliöyhtälön ratkaisujen lukumäärä voidaan erottaa kahdessa tapauksessa, jotka ovat:

1.- Todellisessa määrin

Kun työskentelet todellisilla numeroilla, neliömäiset yhtälöt voivat olla:

-Zero -ratkaisut: Eli ei ole todellista numeroa, joka tyydyttää neliömäistä yhtälöä. Esimerkiksi x²+1 = 0: n annettu yhtälö, ei ole olemassa todellista lukua, joka tyydyttää mainittua yhtälöä, koska molemmat x² ovat suurempia tai yhtä suuret kuin nolla ja 1 on suurempi kuin nolla, joten sen summa on suurempi Tiukka kuin nolla.

-Toistuva ratkaisu: On yksi todellinen arvo, joka tyydyttää neliömäisen yhtälön. Esimerkiksi yhtälön X²-4x+4 = 0 ainoa ratkaisu on x1 = 2.

-Kaksi erilaista ratkaisua: On kaksi arvoa, jotka tyydyttävät neliömäisen yhtälön. Esimerkiksi x²+x -2 = 0: lla on kaksi erilaista ratkaisua, jotka ovat x1 = 1 ja x2 = -2.

2.- Monimutkaisina lukuina

Kun työskentelet monimutkaisten lukujen kanssa, neliömäiset yhtälöt ovat aina kaksi ratkaisua, jotka ovat Z1 ja Z2, joissa Z2 on Z1: n konjugaatti. Lisäksi ne voidaan luokitella seuraavasti:

-Kompleksit: Ratkaisut ovat muodossa z = p ± qi, missä p ja q ovat todellisia lukuja. Tämä tapaus vastaa edellisen luettelon ensimmäistä tapausta.

-Puhtaat kompleksit: Juuri silloin, kun liuoksen todellinen osa on yhtä suuri kuin nolla, toisin sanoen ratkaisussa on muoto z = ± Qi, missä Q on todellinen luku. Tämä tapaus vastaa edellisen luettelon ensimmäistä tapausta.

-Kompleksit, joiden kuvitteellinen osa on yhtä suuri kuin nolla: Juuri kun liuoksen monimutkainen osa on yhtä suuri kuin nolla, toisin sanoen ratkaisu on todellinen luku. Tämä tapaus vastaa edellisen luettelon kahta viimeistä tapausta.

Kuinka neliömäisen yhtälön ratkaisut lasketaan?

Neliömäisen yhtälön ratkaisujen laskemiseksi käytetään kaavaa, joka tunnetaan nimellä ”resoluutio”, jossa sanotaan, että AX²+BX+C = 0 -yhtälön liuokset annetaan seuraavan kuvan lausekkeella:

Neliöjuuren sisällä esiintyvää määrää kutsutaan neliömäisen yhtälön syrjiväksi ja sitä merkitään kirjaimella "d".

Neliöyhtälöllä on:

-Kaksi todellista ratkaisua kyllä, ja vain kyllä, d> 0.

-Toistuva todellinen ratkaisu, jos ja vain jos d = 0.

-Nolla oikeat ratkaisut (tai kaksi monimutkaista ratkaisua) kyllä, ja vain kyllä, D<0.

Esimerkit

-Yhtälön x²+x-2 = 0 ratkaisut annetaan:

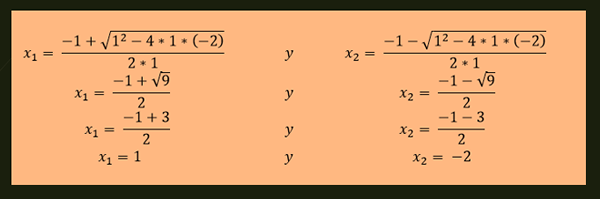
-Yhtälöllä x²-4x+4 = 0 on toistuva ratkaisu, joka annetaan:

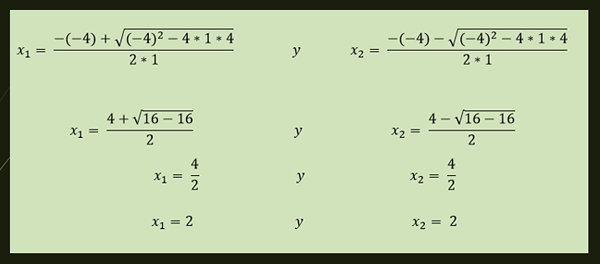
-Yhtälön X²+1 = 0 ratkaisut annetaan:

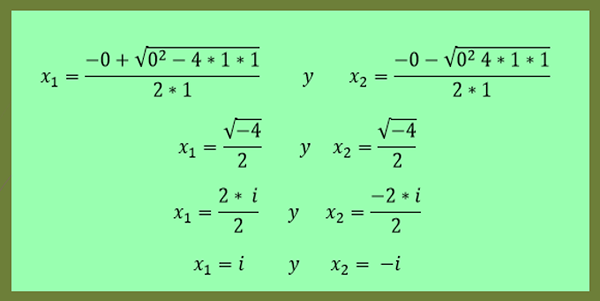
Kuten tässä viimeisessä esimerkissä voidaan nähdä, x2 on x1: n konjugaatti.