Tiheys

Selitämme, mikä on tiheys, sen kaava, kuinka laskea se, olemassa olevat tyypit ja annamme useita esimerkkejä

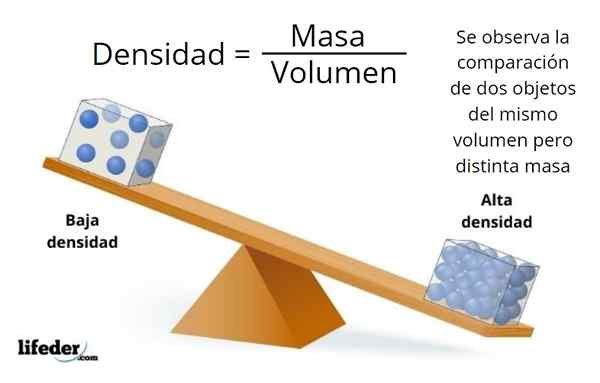
Kahden yhtä suuren määrän kohteen välillä yksi, jolla on suurin tiheys, on suurin massa

Mikä on tiheys?

Se tiheys aineen massa on osamäärä näytteen massan ja sen käyttämän tilavuuden välillä, joka on sen mittayksikkö Kg/M³ Kansainvälisessä yksikköjärjestelmässä. Kreikan kirjainta ρ (Rho) käytetään usein sen merkitsemiseen.

Vesitiheys, joka on yleistä nestettä, on 1000 kg/m³ o 1 g/cm³ 25 ° C: ssa, koska tiheyskokemukset muuttuvat lämpötilan ja paineen myötä.

Monta kertaa on esineitä, joilla on samat mitat, ja silti jotkut ovat kevyempiä ja raskaita, tämä johtuu tiheyseroista. Kevyemmällä esineellä on vähemmän tiheyttä kuin raskain.

Tiheys on aineen intensiivinen ominaisuus, joka ei riipu tutkittavan näytteen massan määrästä, koska samalla aineella pysyy vakiona vakiona. Tämä mahdollistaa aineen erottamisen toisesta.

Materiaaleilla on laaja valikoima tiheyksiä, alaikäiset ovat kaasujen materiaaleja, joten yksikkö kg/m³ Se on erittäin suuri ja grammat/litra tai g/l on edullinen. Muita usein käytettyjä yksiköitä ovat grammat/millilitra tai grammat/kuutio senttimetri.

Tiheyden käsite on erityisen hyödyllinen työskennellessäsi jatkuvilla keinoilla, kuten nesteillä, joko kaasu- tai nesteillä.

Tiheyskaava

Annetun määritelmän mukaan tiheydellä on matemaattinen kaava, jonka on antanut:

Missä tiheys on ρ, m on massa- ja V -tilavuus.

Kuinka tiheys mitataan?

Objektin tiheys voidaan laskea, jos sen massa ja tilavuus mitataan aiemmin. Jälkimmäinen ei ole aina helppoa, koska näyte voi olla epäsäännöllinen, mutta menetelmiä on useita.

Voi palvella sinua: Mars (planeetta)

Geometrinen menetelmä

Jos näytteellä on säännöllinen geometrinen muoto, on kaavoja, jotka sallivat tilavuuden laskemisen sen mittojen perusteella. Mitä taikinaan, tämä voidaan saada tasapainon avulla.

Perustamismenetelmä: Volume siirtymä

Avaimen tilavuuden mittaus siirtymään joutuneella tilavuudella

Jos objekti ei ole säännöllinen, sen tilavuus voidaan määrittää mittaamalla siirtynyt tilavuus, kun se on täysin upotettu nesteeseen, kuten vesi.

Tätä varten käytetään asteittaista astiaa ja sitä täytetään tarkan veden V: n tilavuudella V₁, Sitten objekti on täysin upotettu ja uusi tilavuus V mitataan₂. Objektin tilavuus on yhtä suuri kuin ero v₂ - V₁.

Tämän menetelmän käyttämiseksi näyte -ainetta ei tule liuottaa veteen, ja sinulla on oltava asteittainen astia, jolla on oikean kokoinen.

Tiheys Archimedes -periaatteen kautta

Archimedes -periaatetta voidaan käyttää kiinteän näytteen tiheyden selvittämiseen. Periaatteessa todetaan, että osittainen tai täysin upotettu ruumis läpikäy nousevan voiman, jota kutsutaan pushiksi, jonka suuruus on yhtä suuri kuin siirretyn nesteen paino kehon asettaessa.

Objektin tiheyden määrittämiseksi Archimedes -periaatteen kautta näitä vaiheita noudatetaan:

• Vaihe 1

Määritä massa m_c esineen tasapainon kautta.

• Vaihe 2

Täytä säiliö nesteellä, jonka tiheys tunnetaan, mikä yleensä tislattiin vettä. Tätä arvoa kutsutaan m₁.

• Vaihe 3

Upota astiaan kokonaan vedellä oleva kiinteä esine, huolehtin siitä, etten kosketa seiniä. Havaitaan, että neste käyttää työntövoimaa JA Kiinteällä, ja tämä puolestaan, Newtonin kolmannen lain mukaan, saa aikaan yhtä suuren suuruuden veteen, mutta vastakkaiseen suuntaan.

Voi palvella sinua: Solid State Fysiikka: Ominaisuudet, rakenne, esimerkit

Sarjan punnitsemiseksi saatu arvo, nimeltään M₂, Se on säiliön täynnä vettä enemmän tätä reaktiota.

• Vaihe 4

Tiheyden yhtälöstä voidaan ilmaista kehon tilavuus V, mikä vastaa siirretyn nesteen tilavuutta:

Missä m_c ja ρ_c Kehon massa ja tiheys ovat vastaavasti, kun taas M_F ja ρ_c Ne ovat siirretyn nesteen massa ja tiheys. Tästä lausekkeesta kehon ρ tiheys puhdistetaan_c-

Nesteen häätetyn m massa_F Se on yksinkertaisesti:

m_F = m₂ −m₁

Siksi:

Tiheystyypit

Absoluuttinen tiheys  

Se on aiemmin määritelty tiheys: Massan ja näytteen tilavuuden välinen osuus.

Suhteellinen tiheys

Liian kutsuttu Tietty painovoima, Se on aineen tiheys suhteessa toiseen, jota pidetään referenssinä. Kiinteät aineet ja nesteet tämä vertailuaine on vettä 4 ° C: ssa ja 1 atm paine ja kaasulle se on kuiva ilma. Se lasketaan:

Suhteellinen tiheys = veden veden tiheys/

Sekä materiaalin että veden tiheys on mitattava identtisissä paine- ja lämpötilassa olevissa olosuhteissa ja ilmaista itsensä samoissa yksiköissä.

Seuraava kuva näyttää teräksen ja puun suhteelliset tiheydet.

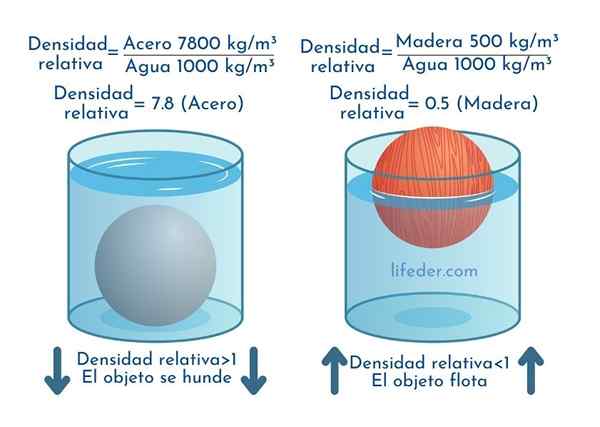
Koska teräksen tiheys on 7800 kg/m³ Ja vesi on 1000 kg/m³, Teräksen suhteellinen tiheys, joka on merkitty SG: ksi, on:

SG = 7800/1000 = 7.8

Puun suhteellinen tiheys on puolestaan:

SG = 500/1000 = 0.5

Esineet, joiden suhteellinen tiheys on vähemmän kuin yksi kelluva vedessä, kun taas ne, joiden suhteellinen tiheys on suurempi kuin yksi pesuallas.

Ilmeinen tiheys

Se lasketaan näytteen massan ja sen tilavuuden välillä, mukaan lukien huokoset ja ilmatilat:

Voi palvella sinua: Satunnainen virhe: kaava ja yhtälöt, laskenta, esimerkit, harjoitukset

Näennäinen tiheys = massa / tilavuus = (massa _hiukkaset + Massa _ilma )/ (Tilavuus _hiukkaset+ Tilavuus _ilma-A

Tiheysesimerkit

• Kaikkien kevyin metalli on litium, 530 kg/m tiheys³
• Veren tiheys on 1060 kg/m³
• Osmium on tunnetuin metalli, tiheys on 22570 kg/m³
• Kvarkkien plasman tiheys on 1 × 10¹⁹ kg/m³

Ratkaisut

Harjoitus 1

Laske korkin tiheys tietäen, että tällä materiaalilla tehty kuutio, joka mittaa 1.5 cm: n puolella on massa 1 g.

• Ratkaisu

Kuution tilavuus on:

V = ℓ³ = (1.5 cm)³ = 3.375 cm³

Lause osoittaa, että kuution massa M on M = 1 g, siten korvata arvot tiheysyhtälössä:

ρ = m / v = 1 g / 3.375 cm³ = 0.296 g/cm³

Harjoitus 2

Mikä on 15 cm: n radiosmiumin valmistettu pallon massa?

• Ratkaisu

Alkaen tiheysyhtälöstä:

Taikina puhdistetaan seuraavasti:

M = ρ ∙ v

On välttämätöntä laskea pallon tilavuus, joka on antanut kaavalla:

Koska pallon säde on. Koska osmiumin tiheys on 22570 kg/m³, On kätevää ilmaista 15 cm metreinä:

R = 15 cm = 15 × 10⁻² m

V = (4/3) π × (15 × 10⁻² m)³ = 0.01414 m³

Tämä arvo korvataan taikinan puhdistuksessa:

M = ρ ∙ V = 22570 kg/m³ × 0.01414 m³ = 319.1 kg

Viitteet

1. Chang, R. 2013. Kemia. 11Va. Painos. McGraw Hill -koulutus.
2. Giancoli, D.  2006. Fysiikka: sovellusten periaatteet. Kuudes. Ed Prentice Hall.
3. Laivamies, J. 2009. Johdanto fysiikkaan. Kahdestoista painos. Brooks/Cole, Cengage Editions.
4. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. McGraw Hill.
5. Antioquian yliopisto. Kiintoaineiden tiheys. Toipunut: Opetus.sinä.Edu.yhteistyö.