Johdettu kotangenttilaskennasta, esittelystä, harjoituksista

Se Kotangentti Se on yhtä suuri kuin sadonkorjuun neliön vastakohta ”-csc²". Tämä kaava johtuu johdannaislakeista määritelmän mukaan ja trigonometristen funktioiden erilaistuminen. Se on merkitty seuraavasti:

D (ctg u) = -csc² tai . du

Missä "du" symboloi argumenttifunktiosta johdettua lauseketta suhteessa riippumattomaan muuttujaan.

Lähde: Pixabay.com

[TOC]

Kuinka se lasketaan?

Näiden johdannaisten kehittämismenettely on melko yksinkertainen. Tunnista vain väite ja sen edustama funktio.

Esimerkiksi lauseke CTG (F/G) esittelee jakautumisen väitteeseen. Tämä tarvitsee erottelun U/V: stä vetoketjun kehittämisen jälkeen.

Kotangentti on tangentin vastavuoroinen funktio. Algebrallisesti tämä tarkoittaa sitä:

(1/tg x) = ctg x

Ctg x = cos x / sen x

On väärin sanoa, että kotangentti funktio on tangentin "käänteinen". Tämä johtuu siitä, että tangentin käänteinen funktio määritelmän mukaan on tangentti kaari.

(TG^-1 x) = arctg x

Pythagoran trigonometrian mukaan kotangentti on mukana seuraavissa osissa:

Ctg x = (cos x) / (sin x)

CTG² X + 1 = CSC² x

Analyyttisen trigonometrian mukaan vastaa seuraaviin identiteetteihin:

Ctg (a + b) = (1 - tg a . Tg b) / (tg a + tg b)

Ctg (a - b) = (1 + tg a . Tg b) / (tg a - tg b)

CTG (2A) = (1 - TG² a) / (2TG A)

Kotangenttitoiminnon ominaisuudet

On tarpeen analysoida funktion f (x) = CTG X: n eri ominaisuuksia, jotta voidaan määritellä tarvittavat näkökohdat sen erottelun ja sovelluksen tutkimiseksi.

Pystysuuntaiset asymptotit

Kohdosta funktiota ei ole määritelty arvoissa, jotka tekevät lausekkeesta "senx" nolla. Vastaavan CTG x = (cos x) / (sin x) johtuen sillä on määrittelemätöntä kaikissa ”nπ”: ssa, jolloin n kuuluu kokonaislukuihin.

Se voi palvella sinua: analyyttinen geometria

Toisin sanoen jokaisessa näissä x = nπ -arvoissa on asymptootti pystysuora. Kun kotangenttien lähestymistavat ja lähestyessäsi oikeaa, funktio kasvaa määräämättömäksi ajaksi.

Verkkotunnus

Kotangenttifunktion domeeni ilmaistaan ​​sarjalla x ∈ R / x ≠ nπ, n ∈ Z. Tätä luetaan nimellä "x, joka kuuluu reaalilukujoukkoon siten, että x eroaa Nπ: stä, n: n kokonaislukujen kanssa" koko numerot ".

Etäisyys

Kotigenttifunktion sijoitus kattaa vähemmän äärettömyyteen. Siksi voidaan päätellä, että sen sijoitus on joukko todellisia N -numeroita.

Taajuus

Cotagent -funktio on jaksollinen ja sen ajanjakso on yhtä suuri kuin π. Tällä tavalla tasa -arvo CTG x = ctg (x + nπ) toteutetaan, missä n kuuluu Z: lle.

Käyttäytyminen

Se on pariton funktio, koska ctg (-x) = - ctg x. Tällä tavoin tiedetään, että funktio esittelee symmetrian koordinaattisen alkuperän suhteen. Siinä on myös väheneminen jokaisessa välissä, joka sijaitsee 2 peräkkäisen pystysuoran asymptoottin välillä.

Sillä ei ole maksimiarvoja tai minimiarvoja, koska niiden lähestymistavat pystysuoraan asymptoottiin on käyttäytymistä, jossa funktio kasvaa tai pienenee toistaiseksi.

Kotigenttifunktion nollat ​​tai juuret löytyvät π/2: n parittomista monikerroksista. Tämä tarkoittaa, että ctg x = 0 täyttyy muodon x = nπ/2 arvoihin kokonaisuudessaan.

Esittely

On 2 tapaa osoittaa kotangenttitoiminnon johdannainen.

Trigonometrinen differentiaalinen esittely

Kohdostajan funktion johdannainen osoitetaan sen vastaavasta rinnassa ja cosenosissa.

Voi palvella sinua: Boolean Algebra: Historia, lauseet ja postulaatit, esimerkit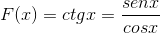

Kyse on funktioiden jaon johdannaisesta

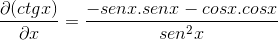
Tekijöiden saamisen jälkeen ryhmitelty ja Pythagorean -identiteettiä pyritään jäljittelemään

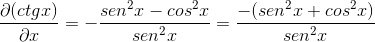
Identiteettien korvaaminen ja vastavuoroisuuden soveltaminen Expression saadaan

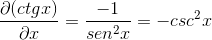
Johdannaisen määritelmän määritelmä

Seuraava lauseke vastaa johdannaista määritelmän mukaan. Jos funktion 2 pisteen välinen etäisyys lähestyy nollaa.

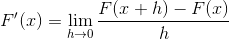
Korvaamalla cotangente, sinun on:

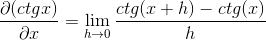
Identiteetit koskevat argumenttien ja vastavuoroisuuden summaa

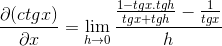
Osoitusosan osuus käytetään perinteisesti

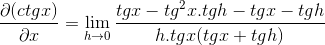
Saadaan vastakkaiset elementit ja piirtäminen yhteinen tekijä

Pythagorean -identiteettien ja vastavuoroisuuden soveltaminen

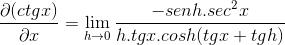
X: ssä arvioidut elementit ovat vakioita rajan suhteen, siksi ne voivat jättää tämän väitteen. Sitten sovelletaan trigonometrisiä rajoja.

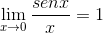
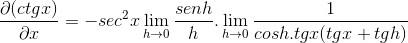
Raja arvioidaan

Sitten se on factoring, kunnes se saavuttaa halutun arvon

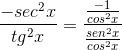
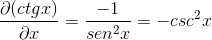
Tämän osoittaa cotangente -johdannainen vastakohtana harvesterin neliön kanssa.

Ratkaisut

Harjoitus 1

Funktion f (x) mukaan määritä lauseke f '(x)

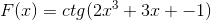
Vastaavaa johdannaista käytetään ketjusäännön kunnioittamiseen

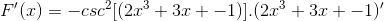
Argumentin saaminen

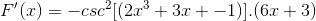
Joskus on tarpeen soveltaa vastavuoroisia tai trigonometrisiä identiteettejä ratkaisujen mukauttamiseksi.

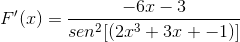
Harjoitus 2

Määritä f (x): tä vastaava differentiaalinen lauseke

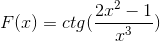
Johdannaisen kaavan mukaan ja ketjusäännön kunnioittaminen

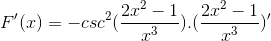
Argumentti on johdettu, kun taas loput pysyvät samoina

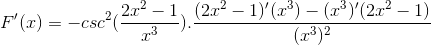
Kaikki elementit

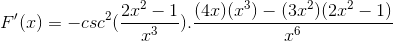
Toimivat perinteisesti saman pohjan tuotteet

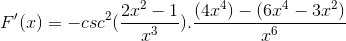
Samat elementit lisätään ja yleinen tekijä uutetaan

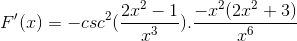
Merkkejä yksinkertaistetaan ja käytetään. Antaa tietä täysin johdetulle ilmaisulle

Voi palvella sinua: ero yhteisen osan ja desimaalin välillä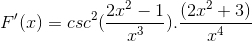

Viitteet

1. Trigonometrinen sarja, nide 1. -Lla. Zygmund. Cambridge University Press, 2002
2. Yhden muuttujan laskenta. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. marraskuuta. 2008
3. Laskenta trigonometrialla ja analyyttisellä geometrialla. John H. Saksi, John Saxon, Frank Wang, Diana Harvey. Saxon Publishers, 1988
4. Monimuuttuja -analyysi. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. joulukuuta. 2010
5. Järjestelmän dynamiikka: Mechatronic -järjestelmien mallintaminen, simulointi ja hallinta. Dekaani C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. maaliskuuta. 2012
6. Laskenta: Matematiikka ja mallinnus. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. tammikuuta. 1999