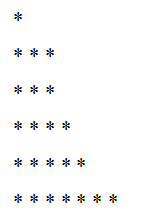Additiivien hajoaminen

Se additiivien hajoaminen positiivisen kokonaisluvun on ilmaista se kahden tai useamman positiivisen määrän summana. Siten meillä on, että numero 5 voi ilmaista sen 5 = 1+4, 5 = 2+3 tai 5 = 1+2+2. Jokainen näistä kirjoitustapoista 5 on se, mitä kutsumme additiiviseksi hajoamiseksi.

Jos kiinnitämme huomiota, voimme nähdä, että lausekkeet 5 = 2+3 ja 5 = 3+2 edustavat samaa koostumusta; Molemmilla on samat numerot. Kuitenkin vain mukavuuden kannalta jokainen mainos on yleensä kirjoitettu kriteereistä vähiten suurimmista.

Additiivien hajoaminen

Toisena esimerkkinä voimme ottaa numeron 27, jonka voimme ilmaista sen seuraavasti:

27 = 7+10+10

27 = 9+9+9

27 = 3+6+9+9

27 = 9+18

Lisäaineen hajoaminen on erittäin hyödyllinen työkalu, jonka avulla voimme vahvistaa tietämystämme numerointijärjestelmistä.

Kaanoninen lisäaineen hajoaminen

Kun meillä on enemmän kuin kahta lukua, tietty hajoamismuoto on 10, 100, 1000, 10 000 jne. Monitoiminnassa, j., jotka tekevät siitä. Tätä minkä tahansa numeron kirjoitustapaa kutsutaan kanoniseksi additiiviseksi hajoamiseksi. Esimerkiksi numero 1456 voi hajottaa sen seuraavasti:

1456 = 1000 + 400+ 50 + 6

Jos meillä on numero 20 846 295, kanoninen additiivien hajoaminen on:

20 846 295 = 20 000 000 + 800 000 + 40 000 + 6000 + 200 + 90 +5.

Tämän hajoamisen ansiosta voimme nähdä, että tietyn numeron arvo annetaan sen aseman perusteella. Otetaan esimerkiksi numerot 24 ja 42:

24 = 20 + 4

42 = 40 +2

Täällä voimme nähdä, että 24: ssä 2: n arvo on 20 yksikköä ja 4: n arvo 4 yksikköä; Toisaalta 42: ssa 4: n arvo on 40 yksikköä ja 2 kahdesta yksiköstä. Siten, vaikka molemmat numerot käyttävät samoja numeroita, niiden arvot ovat täysin erilaisia ​​heidän miehittämänsä aseman mukaan.

Voi palvella sinua: x Squared

Sovellukset

Yksi sovelluksista, jotka voimme antaa additiivisen hajoamiseen.

Esimerkki lause

Otetaan esimerkki seuraavalle lauseelle heidän demonstraatioillaan.

- Olla z kokonaismäärä 4 numeroa, niin Z on jaettavissa viidellä, jos sen luku, joka vastaa yksiköitä, on nolla tai viisi.

Esittely

Muistakaamme, mikä on jaettavuus. Jos meillä on "A" ja "B" kokonaiset numerot, sanomme, että "A" jakaa "B", jos on olemassa kokonaisluku "C" siten, että b = a*c.

Yksi jakautuvuuden ominaisuuksista kertoo meille, että jos "A" ja "B" ovat jaettavissa "C": n välillä, niin myös vähennys "A-B" on.

Olla z kokonaismäärä 4 numeroa; Siksi voimme kirjoittaa Z: lle ja Z = ABCD: lle.

Kanonisen lisäaineen hajoamisen avulla meidän on:

Z = A*1000 + B*100 + C*10 + D

On selvää, että A*1000 + B*100 + C*10 on jaettavissa 5: n välillä. Siksi meillä on, että Z on jaettavissa 5: n välillä, jos z - (a*1000 + b*100 + c*10) on jaettavissa 5: n välillä.

Mutta z - (a*1000 + b*100 + c*10) = d ja d on yksi kuvionumero, joten ainoa tapa olla jaettavissa 5: n välillä on, että se on 0 tai 5.

Siksi Z on jaettavissa 5: n välillä, jos d = 0 tai d = 5.

Huomaa, että jos z: llä on N -numeroita, esittely on täsmälleen sama, se muuttuu vain, että kirjoitamme nyt z = a₁-Lla₂…_n Ja tavoitteena olisi todistaa se_n on nolla tai viisi.

Osiot

Sanomme, että positiivisen kokonaisluvun jakaminen on tapa, jolla voimme kirjoittaa numeron positiivisten kokonaislukujen summana.

Voi palvella sinua: lähentymisradio: Määritelmä, esimerkit ja harjoitukset ratkaistu

Additiivisen hajoamisen ja osion välillä on se, että ensimmäisessä etsitään, että ainakin se voidaan jakaa kahteen tai useampaan, osiossa tämä rajoitus.

Siten meillä on seuraavat:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+2+2

Yllä olevat ovat 5: n osiot.

Eli meillä on, että kaikki lisäaineen hajoaminen on osio, mutta kaikki osiot eivät välttämättä ole lisäaineen hajoamista.

Numeroteoriassa aritmeettisen takeiden peruslause takaa, että jokainen kokonaisluku voidaan kirjoittaa ainutlaatuisesti serkkujen tuotteena.

Kun osioita tutkitaan, tavoitteena on määrittää, kuinka monella tapaa positiivinen kokonaisluku voidaan kirjoittaa muiden kokonaislukujen summana. Siksi määrittelemme osiofunktion, kuten alla esitetään.

Määritelmä

Osion p (n) -toiminto määritellään niiden tapojen lukumääränä, joilla positiivinen kokonaisluku n voidaan kirjoittaa positiivisten kokonaislukujen summana.

Palattuaan viiden esimerkkiin, meidän on:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+1+3

5 = 1+2+2

5 = 1+1+1+2

5 = 1+1+1+1+1

Tällä tavalla p (5) = 7.

Kaaviot

Molemmat osiot että additiiviset hajoamiset numeron n voidaan edustaa geometrisesti.  Oletetaan. Tässä hajoamisessa lisäykset voidaan korjata siten, että summan jäsenet tilataan vähiten suurimmaksi. Joten, se on syytä:

n = a₁ + -lla₂ + -lla₃ +… + A_{r -} kanssa

-lla₁ ≤ a₂ ≤ a₃ ≤ ... ≤ a_{r -}.

Voimme kaavioida sanomalla hajoamisen seuraavasti: Ensimmäisessä rivessä merkitsemme a₁-pisteitä, sitten merkitsemme₂-pisteitä ja niin edelleen, kunnes saavutetaan_{r -}.

Voi palvella sinua: kolmion eriarvoisuus: esittely, esimerkit, ratkaisut harjoitukset

Otetaan esimerkkinumero 23 ja sen seuraava hajoaminen:

23 = 5 + 4 + 7 + 3 + 1 +3

Tilaamme tämän hajoamisen ja meillä on:

23 = 1 + 3 + 3 + 4+ 5 + 7

Sen vastaava kaavio olisi:

Samoin, jos luemme tämän kaavion pystysuoraan sen sijaan vaakasuoraan, voimme saada hajoamisen, joka on mahdollisesti erilainen kuin edellisessä. 23: n esimerkissä seuraava erottuu:

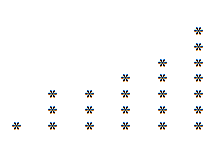
Joten meillä on se 23, voimme myös kirjoittaa sen seuraavasti:

23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.