Kulman siirtymä

Mikä on kulman siirtymä?

Hän Kulman siirtymä Kulma -asennon muutos tai variaatio, jota kiertokokemuksessa oleva esine, yleensä mitattu radiaaneissa tai muussa käännöksissä, kuten arvosanat tai kierrokset.

Kun esine pyörii kiinteän akselin ympärillä, sen kulman siirtymä määritetään mittaamalla kulma, joka pyyhkäisee viivalla, joka kulkee minkä tahansa rungon pisteen läpi leikkaamalla kierto -akselin, ts. Radiaalinen viiva.

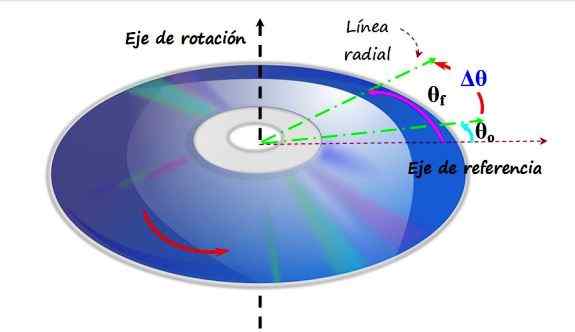Kompakti levy tai CD pyörii antihoranantisuunnassa pystysuoran kierto -akselin ympärillä. Kun kuljet kulmasta θo to θf, sanotaan, että se on kokenut kulman siirtymän. Lähde: f. Zapata.

Yläkuviossa on CD, joka pyörii anti -horaariseen suuntaan, koska se on sen kierto -akseli pystysuuntainen akseli. CD -levyn tasolle asetetaan referenssiakseli, joka vastaa kulmaa 0 radiaania tai 0. Vihreä viiva on säteittäinen viiva, joka muodostaa alun perin kulman θ_jompikumpi Viitteellä. Tämä on alkuperäinen sijainti.

Myöhemmin vihreä viiva siirtyy uuteen sijaintiin nimeltään θ_F, Ja kokenut kokemus, nimeltään Δθ on yksinkertaisesti:

Δθ = θ_F - θ_jompikumpi

Kaikilla CD -arvoilla P kokee saman kulman siirtymisen tietyssä aikaväleissä, lukuun ottamatta keskustaa, missä kierto -akseli kulkee ja pysyy levossa.

Kaavat ja yhtälöt

On esine, joka pyörii kiinteän akselin ympärillä tai joka jättää näytön lukijalle. Ja sen sisällä on piste P, joka sijaitsee kierto -akselin etäisyydellä R ja kuvataan radion R ympärysmielisyydet.

Tämä näkyy seuraavassa kuvassa, joka näyttää leikkausobjektin, joka on nähty kelloulojen vastaisesti. Kyseinen kohta on kulma -asennossa θ, mitattu referenssiakselista, joka tässä tapauksessa on vaaka -akseli.

Voi palvella sinua: Lisäaineperiaate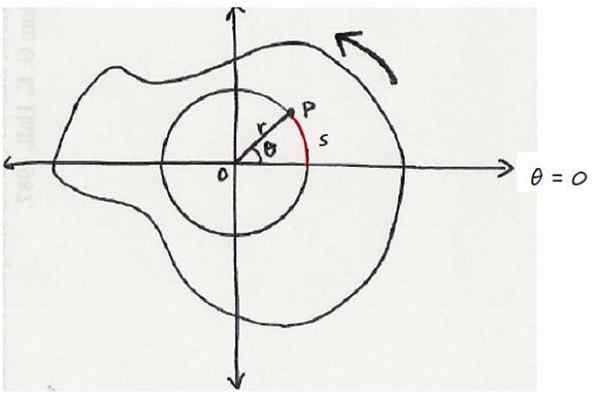Esine, joka pyörii anti -horary -merkityksessä. Kierto -akseli tulee kohtisuoraan näytölle. Lähde: Wikimedia Commons.

Yleissopimuksen mukaan kiertoon antihorariaalisessa mielessä se on annettu positiivinen merkitys, kun taas aikataulun kierto on negatiivinen merkki.

Kun piste P vannoo kulman θ, se kulkee samanaikaisesti kaari. Koska θ on keskeinen kulma, koska sen kärki on ympärysmitta, on täytettävä, että:

Radianina ilmaistuna θ.

Kulman siirtymä on:

Δθ = θ_lopullinen  - θ_alkukirjain

Esimerkiksi, jos p aloitetaan θ: llä_alkukirjain = 0 rad ja sitten on θ_lopullinen = 0.8 Rad, sen kulman siirtymä on peräisin:

Δθ = 0.8 rad - 0 rad =  0 -.8 rad

Muut esineen kohdat voivat käyttää erilaisia ​​kulma -asentoja, mutta kaikki kokevat saman kulman siirtymisen. Keskustan syrjäisimmät hiukkaset kulkevat kuitenkin suurempia etäisyyksiä, koska s = r⋅θ.

Kulmat mittaa

Kiertossa on yleistä löytää radiaaneista mitatut kulmat, mutta niitä löytyy myös asteina ja kierroksissa tai käännöksissä. Ongelmanratkaisussa on tarpeen siirtyä näistä yksiköistä radianeille.

1 vallankumous vastaa täydellistä käännöstä, ts. Kun täydellinen käännös on rikki, se on kääntynyt 360 º ja nämä vastaavat 2π radiaania, koska siinä tapauksessa kohta kierteli kaaria, joka oli yhtä suuri kuin 2πr:

Mutta yksinkertaistaminen, edellinen vastaavuus voidaan ilmaista seuraavasti:

π radianit = 180º

Kuinka kulman siirtymä lasketaan?

Kulmainen siirtymä voidaan laskea analogisesti siihen, kuinka liikkeen siirtyminen lasketaan mittana, tietyn liikemallin jälkeen. Tätä varten keskimääräinen kulmanopeus määritellään kulman siirtymänä Δθ tietyllä aikavälillä Δt:

Missä keskimääräinen kulmanopeus merkitään ω_m ja annetaan radiaaneina/kansainvälisen järjestelmän yksiköissä, jos.

Voi palvella sinua: Kuinka saada kolmion kulma? (Esimerkki)

Välitön kulmanopeus on keskimääräisen kulmanopeuden raja, kun ΔT → 0:

Eli se on ensimmäinen johdettu kulma -asennosta ajankohtana. Kulmakiihtyvyys puolestaan ​​voidaan määritellä, merkitty nimellä α, joka vastaa kulmanopeuden johdannaista tai muutosnopeutta ajan suhteen:

Joka voidaan tulkita myös toiseksi, joka on johdettu kulma -asennosta ajankohtana.

Tärkeää on, että kaksi liikkeen mallia voidaan määrittää analogisesti suoraviivaisten liikkeiden kanssa, koska vaikka kierto suoritetaan tasossa, yksi kulma koordinaatti on riittävä määrittämään minkä tahansa kohteen sijainnin sijainti.

Yhtenäinen pyöreä liike

Yhdenmukaisessa pyöreässä liikkeessä kulmanopeus on vakio, ts. Keskimääräinen kulmanopeus on yhtä suuri kuin välitön kulmanopeus. Koska kulmakiihtyvyys α on yhtä suuri kuin 0, voit kirjoittaa seuraavan yhtälön sijainnille ajan funktiona:

θ = θ_jompikumpi + ωt

Missä θ_jompikumpi Se on matkapuhelimen alkuperäinen sijainti.

Tasaisesti kiihtynyt pyöreä liike

Tässä tapauksessa kulmakiihtyvyys α on vakio, ja analogisesti tasaisesti vaihdetun välittömän liikkeen kanssa voidaan kirjoittaa seuraavat yhtälöt:

• θ = θ_jompikumpi + Ω_jompikumpi T + ½ αt²
• Ω = ω_jompikumpi + αt 
• Ω² = Ω_jompikumpi² + 2α ∙ Δθ

Liikuntaa

Ensimmäinen harjoitus

Voidaan olettaa, että maa on jäykkä esine, joka pyörii kiinteällä akselilla ja että sen kierto on melkein tasainen. Aikavälillä Δt = 12 h löydä:

a) Maan kulman siirtymä

b) kulmanopeutesi

c) kulmakiihtyvyys tuona ajanjakson aikana.

Liittää jhk

Tietäen, että 24 tunnin kuluessa maa kääntää täydellisen käännöksen akselinsa ympäri, 12 tunnissa sinulla on kääntynyt puolet kierroksesta, tsuri π radianit. Jos pidetään sen osaa θ_alkukirjain = 0 rad, sitten sen kulman siirtymä on:

Voi palvella sinua: Moninkertainen periaate: Laskentatekniikat ja esimerkit

Δθ = π radiaanit

Ratkaisu b

Koska kierto on tasaista, kulmanopeus on kulman siirtymän ja ajan välinen osoitus, 1 tunti = 3600 s:

Ω = π rad / 12 h = π rad / (12 x 3600) s = 0.000073 rad/s.

Liuos C

Kulmakiihtyvyys on tyhjä, koska maan kierto on tasainen.

Toinen harjoitus

Juan on kulkenut 35 metrin etäisyyden pyöreällä yleisurheiluradalla, jonka säde on yhtä suuri kuin 7 metriä. Laske Juanin tekemän kulman siirtymä.

Ratkaisu

Koska kuluneen kaarin etäisyys ja kehän säde tunnetaan, toinen kaava voidaan käyttää tuntemaan Juanin tekemä kulma -siirtymä. Yllä kuvattua kaavaa sinun on θ = 35/7 = 5 radiaania.

Kolmas harjoitus

Jos Mario on ajoneuvossaan, puolet pyöreästä kilpa -raidasta, mikä on kulma siirtymä, jonka Mario on tehnyt?

Ratkaisu

Tässä harjoituksessa sovelletaan ensimmäistä kaavaa. Koska tiedetään, että Mario on matkustanut puolet radasta, voidaan olettaa, että hän aloitti kilpailun kulmassa 0 ° ja kun hän saavutti puolet kehästä, hän on matkustanut 180 °. Siksi vastaus on 180 ° -0 ° = 180 ° = π radiaanit.

Neljäs harjoitus

Marialla on pyöreä uima -allas. Koirasi juoksee uima -altaan ympärillä kulkee 18 metrin etäisyydellä. Jos uima -altaan säde on 3 metriä, mikä on Marian lemmikin tekemä kulma -siirtymä?

Ratkaisu

Koska uima -allas on pyöreä ja sen säde on tiedossa, voit jatkaa toisen kaavan käyttöä.

On tiedossa, että säde on yhtä suuri kuin 3 metriä ja lemmikin kuljettama etäisyys on yhtä suuri kuin 18 metriä. Siksi suoritettu kulman siirtymä on yhtä suuri kuin θ = 18/3 = 6 radiaania.

Viitteet

1. Katz, D. 2013. Fysiikka tutkijoille ja insinööreille. Perusteet ja yhteydet. Cengage -oppiminen.
2. Rex, a. 2011. Fysiikan perusteet. Pearson.
3. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1. Pearson.
4. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.
5. Tipler, P. (2006). Fysiikka tieteen ja tekniikan puolesta. 5. ed. Osa 1. Toimitus palautti.