120 jakajaa

Se 120 jakajaa Ne ovat kaikki ne numerot, jotka jakavat sen tarkalleen. Nämä numerot ovat seuraavat:

Jakajat 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, 60, 120

Myös tämän numerosarjan, toisin sanoen negatiiviset, vastustajat ovat 120 jakajaa, koska jako on tarkka. 120: lla on 16 positiivista kokonaista jakajaa ja monia muita negatiivisia.

Numeron jakajia on useita tapoja löytää. Jos tämä ei ole kovin suuri, voit käyttää kertolaskutaulukoita (numeroille alle 100) ja tarkistaa, missä taulukoissa kyseinen numero ilmestyy. Esimerkiksi 12 esiintyy 2, 3, 4 ja 6 taulukoissa, ja nämä ovat heidän jakautumisensa yhdessä yhden ja saman 12: n kanssa.

Lukumäärä voidaan jakaa myös sen ensisijaisiin tekijöihin, soveltaa jaettavuussääntöjä ja kertoa tekijät. Mutta sinun on oltava varovainen, ettet läpäistä mitään huomiotta jätettyä jakajaa.

Koska 120 on suurempi kuin 100, se ei ole suoraan kertolaskutaulukoissa, mutta se ei ole liian työläs löytää sen 16. Kaikkien numeroiden kelvollinen menettely esitetään välittömästi käyttämällä hyvin yksinkertaisia ​​taulukoita.

Kuinka monta jakajaa on 120?

Ensinnäkin 120: n jakajien lukumäärä löytyy. On kaava, jonka avulla voit tietää kuinka monta sinulla on, vaikka se ei sano mitä he ovat.

Yhdistelmäluvut, kuten 120, voidaan ilmaista ensisijaisten lukumäärien tai näiden voimien tuotena. Soittaminen N: lle yhdisteelle:

N = aⁿ ∙ B^m ∙ C^p … R^{k -k -}

Voi palvella sinua: Suhteellisuussuhteet: Konsepti, esimerkit ja harjoitukset

Numerot a, b, c ... r ovat alkulukuja ja n, m, p, ... k, vastaavat voimat. Päätekijöiden hajoaminen 120 on seuraava:

120 | 2
60 | 2
30 | 2
15 | 3
5 | 5
1 | 1

Tällä tavalla 120 on tekijöiden tuote:

120 = 2³ ∙ 3 ∙ 5

Kaava N: n jakajien lukumäärän laskemiseksi

Jakajien lukumäärä = (n +1) × (m +1) × (p +1)… × (k +1)

Nyt sovelletaan kaavaa 120: een. Hajoamisesta tekijöillä, jotka sinun on:

n = 3 (on 2: n voima)

M = 1 (3 on kohonnut arvoon 1: 3¹ = 3)

P = 1 (5 näyttää myös kohotetulta arvoon 1)

Näiden arvojen kanssa:

Jakajien lukumäärä 120 = (3 +1) × (1 +1) × (1 +1) = 4 × 2 × 2 = 16

Tämä tulos osuu samaan aikaan alun alkamisen kanssa: 120: lla on 16 jakajaa. Lisäksi on jo tiedossa, että 2, 3 ja 5 ovat 120: n ja 10: n jakajia, koska mikä tahansa numero 0 on jaettavissa 10: llä. Menettely niiden löytämiseksi kaikki näkyy heti.

120: n jakajien laskenta

Se tehdään edellisessä osassa laskettujen tekijöiden avulla. Siellä nähtiin, että 2 on ensisijainen tekijä eksponentin 3 kanssa ja 3 on toinen serkkukerroin, eksponentin kanssa 1. Näiden tietojen avulla seuraava taulukko on rakennettu:

Huomaa, että 2: n voimat alkavat 2^{0 -} ja päättyy 2³, mikä on tekijä, joka syntyy hajottaessa 120. Muista, että 2^{0 -} ja 3^{0 -} Molemmat ovat yhtä suuret kuin mikä tahansa lukumäärä 0 on 1). Tekijälle 3 alkaa 3^{0 -} Kunnes 3¹, vuodesta 3¹ = 3.

Seuraavaksi taulukko on saatu päätökseen punaisella numeroilla, kuten tässä on esitetty:

Voi palvella sinua: moninkertainen käänteinen: Selitys, esimerkit, ratkaisut harjoitukset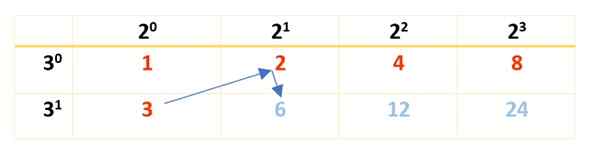

Kaikki punaiset ja siniset numerot ovat 120 jakajaa, mutta niitä on tuskin 8. Jäljellä olevien löytämiseksi uusi taulukko on puhkeaa, jo eturivissä jo saadut jakajat ja kertoimet, jotka on vielä otettava huomioon

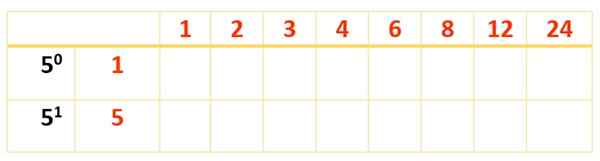
Nyt taulukko on saatu päätökseen punaisten numeroiden tuotteiden kanssa, kuten ensimmäisellä taululla tehtiin:

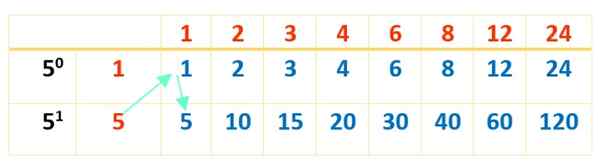
Ja lopuksi 120: n jakautumista sinisellä ilmestyvät. Pöydät ovat erinomainen apu toimintojen tekemisessä järjestyksessä, joten ei 120 jakajaa.

Ratkaisut

Menettely, joka löytää kaikki numeron jakajat, on yhteenveto seuraavasti:

1. Jaamun lukumäärä alkeisiksi tekijöiksi.
2. Laske jakojen lukumäärä kaavan kanssa.
3. Rakenna tarvittavat taulukot jakautujien löytämiseksi. Jos numerolla on kaksi tekijää, taulukko riittää, jos sinulla on kolme tekijää, on tehtävä kaksi taulukkoa, kuten 120: n tapauksessa.

Harjoitus 1

Löydä kaikki 288: n jakajat.

Ratkaisu

288 hajoaa päätekijöiksi:

288 | 2
144 | 2
72 | 2
36 | 2
18 | 2
9 | 3
3 | 3
1 | 1

288 on kirjoitettu näin:

288 = 2⁵ ∙ 3²

Välittömästi on 288: n jakajien lukumäärä:

Jakajien lukumäärä = (n +1) × (m +1) × (p +1)… × (k +1)

Ensisijaisten tekijöiden hajoamisesta on todettu, että n = 5 ja m = 2, sitten:

Jakajat 288 = (5 +1) × (2 +1) = 6 × 3 = 18

Jakajia on 18 ja koska tekijöitä on vain kaksi, se riittää vain yhdellä taulukolla:

Voi palvella sinua: suorakulmion ominaisuudet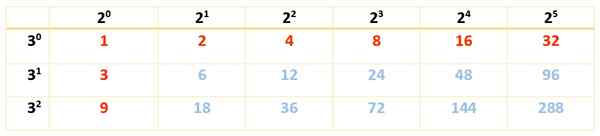

288: n jakajat ovat punaisella ja sinisellä numeroilla:

Div (288) = 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288

Ne voidaan tarkistaa nopeasti laskimen avulla.

Harjoitus 2

Löydä 350: n jakajat

Ratkaisu

350 hajoaa:

350 | 2
175 | 5
35 | 5
7 | 7
1 | 1

350 voidaan kirjoittaa kolmen tekijän tuotteena:

350 = 2 ∙ 5²∙ 7

Seuraava vaihe on laskea, kuinka monta jakajaa on kaavan kautta:

Jakajien lukumäärä = (n +1) × (m +1) × (p +1)… × (k +1)

N = 1, m = 2, p = 1

Jakajat 288 = (1 +1) × (2 +1) × (1 +1) = 2 × 3 × 2 = 12

Koska 350 vaatii kolme tekijää, on tehtävä kaksi pöytää. Ensimmäinen tehdään 2 ja 5², Mutta se voidaan tehdä myös 2 ja 7 tai 7 ja 5², Asetuksen mukaan, koska kaikissa muodoissa lopputulos on sama:

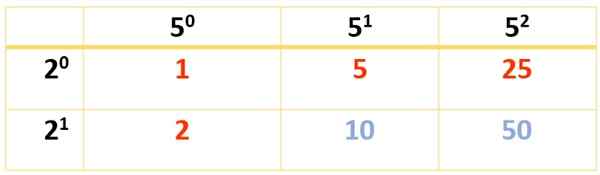
6 jakajaa saadaan. Muut esiintyvät tämän toisen taulukon avulla:

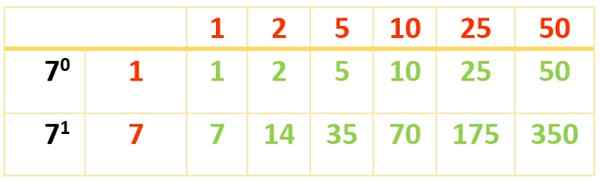
350: n jakajat ovat:

Div (350) = 1, 2, 5, 7, 10, 14, 25, 35, 50, 70, 175, 350