Funktion verkkotunnus ja ristiriita (esimerkkien kanssa)

Käsitteet toiminnon verkkotunnus ja ristiriita Niitä opetetaan yleisesti yliopiston uran alussa opetetuissa laskentakursseissa.

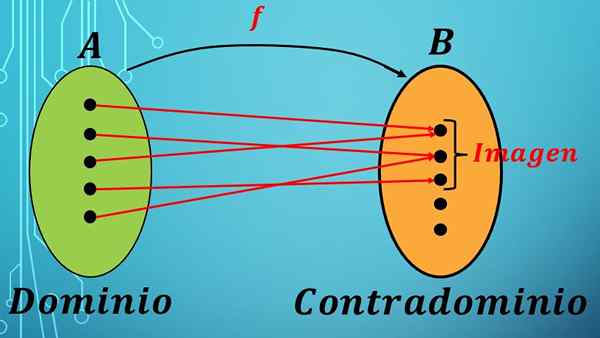
Ennen verkkotunnuksen ja ristiriidan määrittelyä sinun pitäisi tietää, mikä on toiminto. F -funktio on kirjeenvaihtolaki (sääntö) kahden sarjan elementtien välillä.

Koko, jota elementit valitaan.

Matematiikassa A -alue A: n ja ristiriitaisen B funktio merkitään lausekkeella F: A → B.

Edellisessä lausekkeessa sanotaan, että sarjan A elementit lähetetään asettamaan B kirjeenvaihtolain F mukaisesti.

Toiminto määrittää sarjan jokaisen elementin yhdeksi sarjan B elementille.

Verkkotunnus ja ristiriita

Kun otetaan huomioon todellisen muuttujan F (x) todellinen funktio, funktion alueen on oltava kaikki nämä reaaliluku.

Yleensä funktion ristiriita on todellisten N -numerot. Ristiriitaa kutsutaan myös F -funktion saapumis- tai codominium -joukkoksi.

Funktion ristiriita on aina r?

Ei. Niin kauan kuin funktiota ei tutkita yksityiskohtaisesti, todellisten N -numeroiden joukko pidetään yleensä ristiriidana.

Mutta kun funktio on tutkittu, sopivampi joukko voidaan pitää ristiriitaisena, joka on R: n osajoukko.

Edellisessä kappaleessa mainittu asianmukainen joukko osuu samaan aikaan funktion kuvan kanssa.

Funktion f kuvan tai alueen määritelmä viittaa kaikkiin arvoihin, jotka tulevat arvon elementin arvioinnista F: ssä.

Verkkotunnus ja ristiriitaiset esimerkit

Seuraavissa esimerkeissä on havainnollistettu kuinka laskea funktion ja sen kuva.

Esimerkki 1

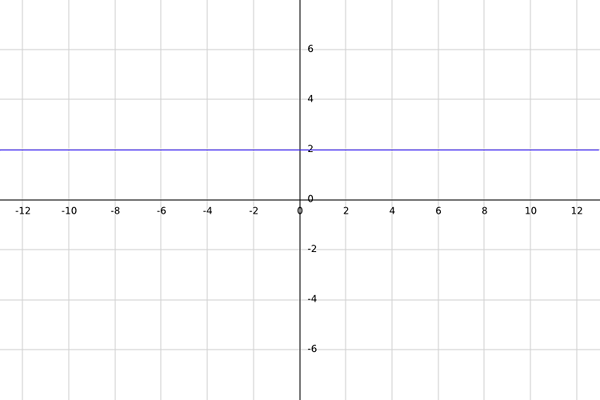
Olkoon f todellinen funktio, jonka määrittelee f (x) = 2.

F: n m -domain on kaikki todelliset numerot siten, että arvioitaessa niitä F: ssä, tulos on todellinen luku. Ristiriita tällä hetkellä on yhtä suuri kuin r.

Koska annettu funktio on vakio (aina yhtä suuri kuin 2), sen on riippumatta siitä, mikä reaaliluku on valittu, koska sen arvioitaessa tulos on aina yhtä suuri kuin 2, mikä on todellinen luku.

Siksi annetun funktion alue on kaikki todellisia lukuja; eli a = r.

Nyt kun on jo tiedossa, että funktion tulos on aina yhtä suuri kuin 2, funktion kuva on vain numero 2, joten funktion ristiriita voidaan määritellä uudelleen b = img (f) = 2.

Siksi f: r → 2.

Esimerkki 2

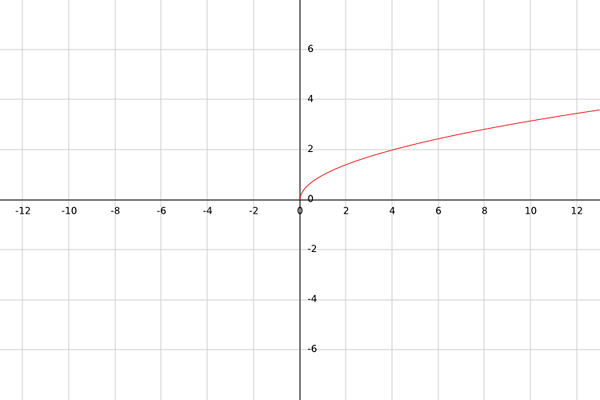
Olkoon g g (x) = √x määrittelemä todellinen funktio, joka on määritelty.

Niin kauan kuin G: n kuvaa ei tiedetä, G: n ristiriita on B = R.

Tällä toiminnolla on otettava huomioon, että neliöjuuret määritetään vain ei -negatiivisille lukuille; toisin sanoen lukumäärälle, joka on suurempi tai yhtä suuri kuin nolla. Esimerkiksi √-1 ei ole todellinen numero.

Siksi G -funktion hallinnan on oltava kaikki luvut, jotka ovat suurempia tai yhtä suuret kuin nolla; eli x ≥ 0.

Siksi a = [0,+∞).

Alueen laskemiseksi on huomattava, että g (x): n tulos, koska se on neliöjuuri, on aina suurempi tai yhtä suuri kuin yhtä suuri kuin. Eli b = [0,+∞).

Yhteenvetona voidaan todeta, että G: [0,+∞) → [0,+∞).

Esimerkki 3

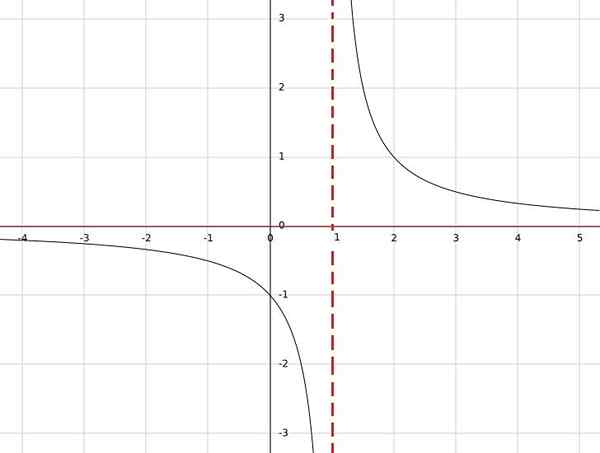
Jos sinulla on funktio H (x) = 1/(x-1), tätä toimintoa ei ole määritelty x = 1: lle, koska nimittäjässä se saadaan nolla ja jakautumista nollalla ei ole määritelty.

Toisaalta, mikä tahansa muu todellinen arvo, tulos on todellinen numero. Siksi verkkotunnus ovat kaikki reakisia paitsi yksi; eli a = r \ 1.

Samoin voidaan nähdä, että ainoa arvo, jota ei voida saada seurauksena.

Siksi funktion kuva on kaikkien reakisten sarja paitsi nolla, niin sitä pidetään ristiriitaisena b = r 0.

Yhteenvetona voidaan todeta, että H: r \ 1 → r \ 0.

Havainnot

Verkkotunnuksen ja kuvan ei tarvitse olla sama sarja, kuten esimerkeissä 1 ja 3 osoitetaan.

Kun funktio on kuvaaja Cartesian -tasolla, domeenia edustaa X -akseli ja ristiriita tai alue edustaa Y -akselia.