Ensimmäisen luokan yhtälöiden kaava, kuinka ratkaista ne, esimerkki, harjoitukset

Se Ensimmäisen asteen tai lineaariset yhtälöt Tuntemattomien kanssa ovat ne, jotka voidaan ilmaista kahden termin summana seuraavalla tavalla:

kirves + b = 0

Missä A ja B, kanssa -lla ≠ 0, ovat reaalilukuja r tai myös kompleksit c. Sen ratkaisemiseksi termit siirretään, mikä tarkoittaa termien vaihtamista tasa -arvosta toiselle.

Kuvio 1. Lineaarinen yhtälö on y = mx + c -muoto y = 0: lla. Lähde: Pxhere.

Tuntemattoman puhdistamiseksi termi +b siirretään, jonka on mentävä tasa -arvon oikealle puolelle muutettulla merkinnällä.

AX = -B

Sitten x: n arvo tyhjennetään tällä tavalla:

x = - b/a

Esimerkiksi ratkaisemme seuraavan yhtälön:

6x - 5 = 4

Siirrämme termin -5 oikealle puolelle muutetulla merkkillä:

6x = 4 + 5

Tämä vastaa 5: n lisäämistä alkuperäisen yhtälön molemmille puolille:

6x - 5 + 5 = 4 + 5 → 6x = 9

Ja nyt puhdistamme tuntemattoman "x":

x = 9/6 = 3/2

Mikä vastaa tasa -arvon molempien puolien jakamista 6: lla. Joten voimme arvioida seuraavan ratkaisun saamiseksi:

-Sama määrä voidaan lisätä tai vähentää yhtälön tasa -arvon molemmat puolet muuttamatta sitä.

-Voit myös moninkertaistaa (tai jakaa) samalla määrällä kaikki yhtälön vasemmalla että oikealla puolella olevat termit.

-Ja jos yhtälön molemmat jäsenet nousevat samaan valtaan, tasa -arvoa ei myöskään muuteta.

[TOC]

Kuinka ratkaista ensimmäisen asteen yhtälöt

Ensimmäisen asteen yhtälön ratkaisu tunnetaan myös nimellä saman. Se on x: n arvo, joka muuntaa alkuperäisen lausekkeen tasa -arvoksi. Esimerkiksi:

5x = 8x - 15

Jos korvaamme x = 5 tässä yhtälössä, se saadaan:

5⋅5 = 8⋅5 - 15

25 = 40 - 15

25 = 25

Koska ensimmäisen asteen lineaariset yhtälöt tulevat monin tavoin, jotka eivät joskus ole ilmeisiä, on joukko yleisiä sääntöjä, jotka käsittävät useita algebrallisia manipulaatioita tuntemattoman arvon löytämiseksi:

-Ensinnäkin, jos on ilmoitettu, ne on suoritettava.

-Ryhmittely symbolit, kuten sulkut, neliömäiset kiinnikkeet ja avaimet, jos niitä on, on tukahdutettava ylläpitämällä asianmukaisia ​​merkkejä.

-Termit siirretään asettamaan kaikki ne, jotka sisältävät tuntemattoman yhdelle tasa -arvon puolelle, ja ne, jotka eivät sisällä sitä toiselle.

-Sitten kaikki samanlaiset termit vähenee, jotta muodostuu lomakkeeseen AX = -B.

-Ja viimeinen askel on puhdistaa tuntematon.

Graafinen tulkinta

Alussa nostettu ensimmäisen asteen yhtälö voidaan johtaa linjan y = mx+c yhtälöstä, tekemällä y = 0. Tulosten arvon arvo vastaa viivan leikkausta vaaka -akselin kanssa.

Seuraavassa kuvassa sinulla on kolme riviä. Alkaen vihreästä viivasta, jonka yhtälö on:

Voi palvella sinua: tekijä

y = 2x - 6

Y = 0: n tekeminen linjan viivalla ensimmäisen asteen yhtälö saadaan:

2x - 6 = 0

Jonka ratkaisu on x = 6/2 = 3. Nyt kun kuvaamme kuvaajaa, on helppo ymmärtää, että käytännössä viiva leikkaa vaakasuoraan akseliin kohdassa x = 3.

Sininen viiva leikkaa x -akselin x = 5: ssä, joka on liuos yhtälöön -x + 5 = 0. Lopuksi linja, jonka yhtälö on y = 0.5x + 2 Leikkaa x -akseliin x = -4, jota varoitetaan helposti ensimmäisen asteen yhtälöstä:

0 -.5 x + 2 = 0

x = 2/0.5 = 4

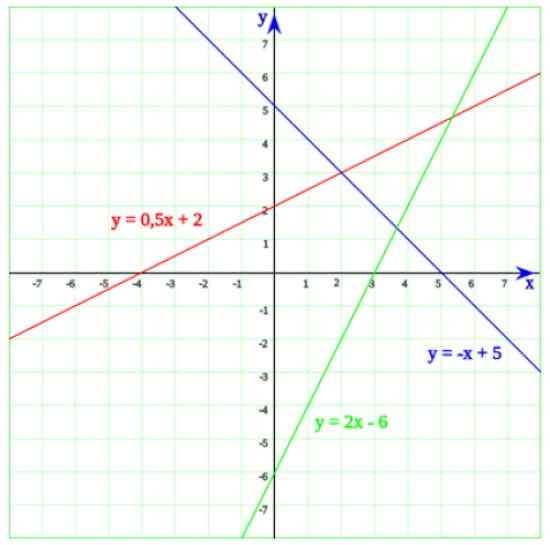Kuva 2. Kolme riviä, joiden risteykset vaakasuoran akselin kanssa vastaavat lineaarisia yhtälöitä. Lähde: Wikimedia Commons.

Esimerkkejä yksinkertaisista lineaarisista yhtälöistä   

Kokonaiset yhtälöt

He ovat niitä, joiden nimittäjiä ei ole esimerkiksi nimittäjiä:

21 - 6x = 27 - 8x

Sen ratkaisu on:

-6x + 8x = 27 - 21

2x = 6

x = 3

Murto -yhtälöt

Nämä yhtälöt sisältävät ainakin yhden eri nimittäjän 1. Niiden ratkaisemiseksi se on suositeltavaa.

Seuraava yhtälö on murto -tyyppi:

Nimittäjät ovat 6, 8 ja 12 ja niiden vähimmäisvaatimukset, jotka on merkitty m: ksi.c.M (6, 8,12) on pienin näistä nimittäjistä sisältävistä numeroista.

Koska nämä numerot ovat pieniä, ei ole vaikea nähdä sitä.c.M (6, 8,12) = 24. Tämä tulos saadaan helposti ilmaisemalla numerot ensisijaisten tai niiden voimien tuotteena, katsotaan:

6 = 3.2

8 = 2³

12 = 2²⋅3

Pienin yleinen monikerros määritetään kertomalla 6, 8 ja 12 yleiset ja ei -yleisökertoimet suurimmalla eksponentillaan: sitten:

MCM (6,8,12) = 2³ ⋅3 = 8 × 3 = 24

Koska vähimmäismäärä on saatavana, se on kerrottava jokaisella yhtälön ehdolla:

Tällä tavoin nimittäjiä tukahdutetaan ja tuotteilla on yhtälö, joka on helpompi ratkaista:

4 (x+5) -3 (2x+3) = 2 (1-5x)

Käytämme jakautuvaa omaisuutta:

4x + 20 - 6x -9 = 2 - 10x

Kaikki termit, jotka sisältävät tuntemattoman "X", on ryhmitelty tasa -arvon vasemmalle puolelle jättäen oikean puolen riippumattomat tai numeeriset ehdot:

4x - 6x + 10 x = 2 +9 - 20

8x = -9

x = - 9/8

Kirjaimelliset yhtälöt

Ne ovat lineaarisia yhtälöitä tuntemattomilla, joihin liittyy kuitenkin kirjaimellisia kertoimia (kirjaimia). Näitä kirjaimia kohdellaan aivan kuten se tehdään numeroilla. Esimerkki kirjaimellisesta ensimmäisen asteen yhtälöstä on:

-3AX + 2A = 5x - B

Tämä yhtälö ratkaistaan ​​samalla tavalla kuin jos riippumattomat termit ja kertoimet olisivat numeerisia:

-3AX - 5x = - b - 2a

Factoring tuntematon "x":

x (-3a - 5) = - b - 2a

x = ( - b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)

Ensimmäisen asteen yhtälöjärjestelmät 

Yhtälöjärjestelmät koostuvat yhtälöistä, joissa on kaksi tai useampia tuntemattomia. Järjestelmäratkaisu koostuu arvoista, jotka tyydyttävät yhtälöt samanaikaisesti ja määrittämään sen yksiselitteisesti, on oltava yhtälö jokaiselle tuntemattomalle.

Voi palvella sinua: Vector Algebra

Järjestelmän yleinen muoto m Lineaariset yhtälöt n tuntemattomat on:

-lla_yksitoistax₁ + -lla₁₂x₂ +…_1nx_n = b₁
-lla_{kaksikymmentäyksi}x₁ + -lla₂₂x₂ +…_2Nx_n = b₂
..
-lla_M1x₁ + -lla_m2x₂ +…_mnx_n = b_m

Jos järjestelmällä on ratkaisu, sanotaan, että se on yhteensopiva, Kun se on ääretön arvojoukko, se on määrittelemätön yhteensopiva, Ja lopuksi, jos sillä ei ole ratkaisua, niin se on yhteensopimaton.

Lineaaristen yhtälöjärjestelmien resoluutiossa käytetään useita menetelmiä: pelkistäminen, korvaaminen, tasaaminen, graafiset menetelmät, Gauss-Jordanin eliminaatio ja determinanttien käyttö ovat eniten käytettyjä. Mutta ratkaisun saavuttamiseksi on muita algoritmeja, jotka ovat helpompia järjestelmille, joissa on monia yhtälöitä ja tuntemattomia.

Esimerkki lineaaristen yhtälöiden järjestelmästä kahdella tuntemattomalla on:

8x - 5 = 7y - 9
6x = 3y + 6

Tämän järjestelmän ratkaisu toimitetaan myöhemmin ratkaistuissa harjoitusosassa.

Lineaariset yhtälöt absoluuttisella arvolla

Todellisen numeron absoluuttinen arvo on etäisyys sen sijainnin välillä numeroviivalla ja sen 0. Etäisyys sen arvo on aina positiivinen.

Numeron absoluuttinen arvo on merkitty moduulipalkeilla: │x│. Esimerkiksi positiivisen tai negatiivisen luvun absoluuttinen arvo on aina positiivinen:

│+8│ = 8

│-3│ = 3

Absoluuttisen arvon yhtälössä tuntematon on moduulipalkkien välillä. Harkitse seuraavaa yksinkertaista yhtälöä:

│X│ = 10

On olemassa kaksi mahdollisuutta, ensimmäinen on, että X on positiivinen luku, jolloin meillä on:

x = 10

Ja toinen mahdollisuus on, että X on tässä tapauksessa negatiivinen luku:

x = -10

Nämä ovat tämän yhtälön ratkaisut. Katsotaanpa nyt erilainen esimerkki:

│X+6│ = 11

Sitten palkkien määrä voi olla positiivinen, sitten:

x+6 = 11

x = 11 -6 = 5

Tai voi olla negatiivinen. Siinä tapauksessa:

-(x+6) = 11

-x - 6 = 11 ⇒ -x = 11+6 = 17

Ja tuntemattoman arvo on:

x = -17

Tällä absoluuttisella arvoyhtälöllä on siis kaksi ratkaisua: x₁ = 5 ja x₂ = -17. Voimme varmistaa, että molemmat ratkaisut johtavat tasa -arvoon alkuperäisessä yhtälössä:

│5+6│ = 11

│11│ = 11

JA

│-17+6│ = 11

│-11│ = 11

Yksinkertaiset ratkaisut

- Harjoitus 1

Ratkaise seuraava lineaaristen yhtälöiden järjestelmä kahdella tuntemattomalla:

8x - 5 = 7y -9
6x = 3y + 6

Ratkaisu

Koska tämä järjestelmä on nostettu, se soveltuu korvausmenetelmän käyttöön, koska toisessa yhtälössä tuntematon x Se on melkein valmis puhdistukseen:

x = (3y + 6)/6

Voi palvella sinua: algebrallinen

Ja voit korvata heti ensimmäisen yhtälön, josta tulee sitten ensimmäinen aste yhtälö tuntemattomalla "Y":

8 [(3y + 6)/6] - 5 = 7y - 9

Nimittäjää voidaan tukahduttaa, jos jokainen termi kerrotaan 6:

6 . 8⋅ [(3y + 6)/6] - 6.5 = 6 .7y- 6 . 9

8⋅ (3y + 6) - 30 = 42y - 54

Jakautuvan ominaisuuden soveltaminen ensimmäisellä termillä tasa -arvo oikealle:

24y + 48 -30 = 42y - 54 ⇒ 24y + 18 = 42y - 54

Yhtälöä voidaan yksinkertaistaa, koska kaikki kertoimet ovat 6: 6:

4y + 3 = 7y - 9

-3y = -12

y = 4

Tällä tuloksella siirrymme X: n puhdistumiseen:

x = (3y +6)/6 → x = (12 +6)/6 = 3

- Harjoitus 2

Ratkaise seuraava yhtälö:

Ratkaisu

Tässä yhtälössä tuotteet ilmestyvät, ja alussa annettujen ohjeiden mukaisesti niitä on ensin kehitettävä:

3x - 10x +14 = 5x + 36x + 12

Sitten kaikki tuntemattomat termit kuljetetaan tasa -arvon vasemmalle puolelle, ja oikealla puolella riippumattomat termit ovat:

3x - 10x - 5x - 36x = 12 - 14

-48x = -2

x = 1/24

- Harjoitus 3

Lisäämällä kolmion kolme sisäkulmaa, saadaan 180º. Suurin ylittää lapsen 35º: ssa, ja tämä puolestaan ​​ylittää 20º: n suurimman ja väliaineen välisen eron. Mitkä ovat kulmat?

Ratkaisu

Kutsumme "x" pääkulmaan, "y" medialle ja "z" lapselle. Kun lausunnossa todetaan, että niiden summa on 180º, voit kirjoittaa:

x + y + z = 180

Sitten tiedämme, että vanhin ylittää lapsen 35º: ssa, voimme kirjoittaa tämän:

X = z + 35

Lopuksi lapsi ylittää 20 º: n suurimman ja väliaineen väliseen eroon:

Z = x - y + 20

Meillä on 3 yhtälön ja 3 tuntemattoman järjestelmä:

x + y + z = 180

X = z + 35

Z = x - y + 20

Tyhjentämällä ensimmäinen yhtälö, sinulla on:

Z = 180 - x - y

Vastaa kolmannen:

180 - x - y = x - y + 20

Vasemman puolen tuntemattomien ohittaminen kuten aina:

-x - y - x + y = 20 - 180

"Y" peruutetaan ja pysyy:

-2x = - 160

x = 80º

Toinen yhtälö on z: n arvo:

Z = x - 35 = 80 - 35 = 45º

Ja ensimmäisen tai kolmannen arvon arvo ja se on:

y = 180 - x - z = 180 - 80 - 45 = 55º

Viitteet

1. Kalju. 1977. Perusalgebra. Venezuelan kulttuuriversiot.
2. Monterey Institute. Yhtälöt, eriarvoisuus ja absoluuttinen arvo. Toipunut: Montereyinstitute.org.
3. Verkkoopettaja. Lineaarisen tai ensimmäisen asteen yhtälöiden luokittelu. Toipunut: professori inline.Cl.
4. Hoffman, J. Matematiikan aiheiden valinta. Nide 2.
5. Jiménez, r. 2008. Algebra. Prentice Hall.
6. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.