Polynomiset yhtälöt

Mitkä ovat polynomiyhtälöt?

Se Polynomiset yhtälöt Ne ovat lausunto, joka nostaa kahden lausekkeen tai jäsenen tasa -arvon, jossa ainakin yksi termeistä, jotka muodostavat tasa -arvon molemmat puolet, ovat polynomit P (x). Nämä yhtälöt on nimetty niiden muuttujien asteen mukaan.

Yleensä yhtälö on lausunto, joka vahvistaa kahden lausekkeen tasa -arvon, jossa ainakin yhdellä näistä on tuntemattomia määriä, joita kutsutaan muuttujiksi tai tuntemattomiksi. Vaikka yhtälöitä on monen tyyppisiä, ne luokitellaan yleensä kahteen tyyppiin: algebrallinen ja transsendentti.

Polynomiset yhtälöt sisältävät vain algebrallisia lausekkeita, joilla voi olla yksi tai useampi tuntematon, joka puuttuu yhtälössä. Heidän eksponentin (luokan) mukaan ne voidaan luokitella: ensimmäisen luokan (lineaarinen), toinen luokka (neliömäinen), kolmas luokka (kuutio), neljäs luokka (kvantic), jonka aste on suurempi tai yhtä suuri kuin viisi ja viisi irrationaalinen.

Polynomiyhtälöiden ominaisuudet

Polynomiset yhtälöt ovat lausekkeita, jotka muodostuvat kahden polynomin välisellä tasa -arvolla; Toisin sanoen tuntemattomien arvojen (muuttujat) ja kiinteiden lukujen (kertoimet) välillä, joissa muuttujilla voi olla eksponentteja, ja niiden arvo voi olla positiivinen kokonaisluku, mukaan lukien nolla.

Eksponentit määrittävät yhtälön asteen tai tyypin. Tämä lausekkeen termi, jolla on eniten arvonlehdenottoa, edustaa polynomin absoluuttista astetta.

Polynomisia yhtälöitä tunnetaan myös algebrallisina, niiden kertoimet voivat olla todellisia tai kompleksisia lukuja ja muuttujat ovat tuntemattomia numeroita, joita edustavat kirjain, kuten: "x".

Jos korvaamalla arvo muuttujalla "x" p (x): ssä tulos on yhtä suuri kuin nolla (0), sanotaan, että tämä arvo täyttää yhtälön (se on ratkaisu) ja sitä kutsutaan yleensä polynomijuuriksi.

Kun polynomiyhtälö kehitetään, kaikki juuret tai ratkaisut haluavat löytää.

Polynomiyhtälöiden tyypit

Polynomiyhtälöitä on useita tyyppejä, jotka erotetaan muuttujien lukumäärän mukaan, ja myös niiden eksponentin asteen mukaan.

Siten polynomiyhtälöt -missä sen ensimmäinen termi on polynomi, jolla on vain yksi tuntematon, kun otetaan huomioon, että sen aste voi olla mikä tahansa luonnollinen luku (n) ja toinen termi on nolla -voi ilmaista seuraavasti:

Voi palvella sinua: trigonometrian historia sen alkuperästä

-lla_{N *} xⁿ + -lla_{N-1 *} x^N-1 +… + A_{1 *} x¹ + -lla_{0 *} x_{0 -} = 0

Missä:

• -lla_n, -lla_N-1 jo_{0 -}, Ne ovat todellisia kertoimia (numerot).
• -lla_n on erilainen kuin nollasta.
• Eksponentti N on positiivinen kokonaisluku, joka edustaa yhtälöastetta.
• X on muuttuja tai tuntematon, jota on etsittävä.

Polynomiyhtälön absoluuttinen tai suurempi aste on suuremman arvon eksponentti kaikkien niiden joukossa, jotka muodostavat polynomia; Tällä tavoin yhtälöt luokitellaan seuraavasti:

Ensiluokkainen

Ensimmäisen asteen polynomiyhtälöt, jotka tunnetaan myös nimellä lineaariset yhtälöt, ovat ne, joihin aste (suurin eksponentti) on yhtä suuri kuin 1, polynomi on muodossa P (x) = 0; Ja se koostuu lineaarisesta ja riippumattomasta termistä. Se on kirjoitettu seuraavasti:

kirves + b = 0.

Missä:

• A ja B ovat todellisia numeroita ja ≠ 0.
• Kirves on lineaarinen termi.
• B on riippumaton termi.

Esimerkiksi yhtälö 13x - 18 = 4x.

Lineaaristen yhtälöiden ratkaisemiseksi kaikki tuntemattoman X: n termit on siirrettävä tasa -arvon puolelle, ja termit, joilla ei ole toisella puolella liikkumista, sen puhdistamiseksi ja ratkaisun hankkimiseksi:

13x - 18 = 4x

13x = 4x + 18

13x - 4x = 18

9x = 18

x = 18 ÷ 9

x = 2.

Tällä tavalla annetussa yhtälössä on vain yksi ratkaisu tai juuri, joka on x = 2.

Toinen luokka

Toisen asteen polynomiyhtälöt, jotka tunnetaan myös nimellä neliömäiset yhtälöt, ovat ne, joissa aste (suurin eksponentti) on yhtä suuri kuin 2, polynomi on muodossa P (x) = 0, ja se koostuu kvadraattisesta termistä, a lineaarinen ja itsenäinen. Se ilmaistaan ​​seuraavasti:

kirves² + BX + C = 0.

Missä:

• A, B ja C ovat todellisia numeroita ja A ≠ 0.
• kirves² Se on neliöllinen termi ja "A" on neliömäisen termin kerroin.
• BX on lineaarinen termi, ja “B” on lineaarisen termin kerroin.
• C on riippumaton termi.

Päättäväinen

Yleensä ratkaisu tämän tyyppisiin yhtälöihin annetaan yhtälön x puhdistamisessa, ja se pysyy seuraavasti, jota kutsutaan päättäväiseksi:

Voi palvella sinua: binomitese

Siellä (b² - 4AC) kutsutaan syrjiksi yhtälöstä ja tämä lauseke määrittää ratkaisujen lukumäärän, jotka yhtälöllä voi olla:

• Kyllä B² - 4AC) = 0, yhtälöllä on yksi kaksinkertainen ratkaisu; eli siinä on kaksi yhtä suurta ratkaisua.
• Kyllä B² - 4AC)> 0, yhtälöllä on kaksi erilaista todellista ratkaisua.
• Kyllä B² - 4ac) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).

Esimerkiksi sinulla on 4x -yhtälö² + 10x - 6 = 0, sen ratkaisemiseksi ensin tunnistetaan termit A, B ja C, ja sitten se korvataan kaavassa:

A = 4

B = 10

C = -6.

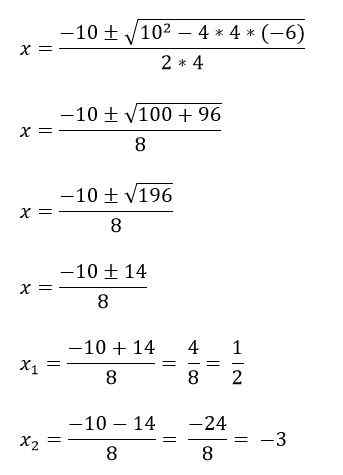
On tapauksia, joissa toisen asteen polynomiyhtälöillä ei ole kolmea termiä, ja siksi ne ratkaistaan ​​eri tavalla:

• Jos neliömäiset yhtälöt eivät ole lineaarista termiä (ts. B = 0), yhtälö ilmaistaan ​​kirveenä² + C = 0. Sen ratkaisemiseksi X puhdistetaan² Ja neliöjuuret sovelletaan kussakin jäsenessä, muistaen, että kaksi mahdollista merkkiä, jotka tuntemattomat voivat olla:

kirves² + C = 0.

x² = - c ÷ a

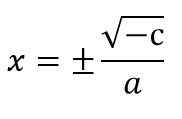
Esimerkiksi 5 x² - 20 = 0.

5 x² = 20

x² = 20 ÷ 5

x = ± √4

x = ± 2

x₁ = 2.

x₂ = -2.

• Kun neliömäisessä yhtälössä ei ole riippumatonta termiä (ts. C = 0), yhtälö ilmaistaan ​​kirveenä² + BX = 0. Sen ratkaisemiseksi on otettava tuntemattoman X: n yleinen tekijä ensimmäisessä jäsenessä; Koska yhtälö vastaa nollaan, on täytettävä, että ainakin yksi tekijöistä on yhtä suuri kuin 0:

kirves² + BX = 0.

x (ax + b) = 0.

Tällä tavalla sinun on:

x = 0.

x = -b ÷ a.

Esimerkiksi: Sinulla on yhtälö 5x² + 30x = 0. Ensinnäkin se on tekijä:

5x² + 30x = 0

x (5x + 30) = 0.

Syntyy kaksi tekijää, jotka ovat x y (5x + 30). Yksi näistä pidetään nollaan ja toiselle annetaan ratkaisu:

x₁ = 0.

5x + 30 = 0

5x = -30

x = -30 ÷ 5

x₂ = -6.

Korkein luokka

Pääasteen polynomiyhtälöt ovat ne, jotka vaihtelevat kolmannesta luokasta, jotka voidaan ilmaista tai ratkaista yleisen polynomiyhtälön kanssa millä tahansa asteella:

Voi palvella sinua: Korrelaatiokerroin: kaavat, laskenta, tulkinta, esimerkki

-lla_{N *} xⁿ + -lla_{N-1 *} x^N-1 +… + A_{1 *} x¹ + -lla_{0 *} x_{0 -} = 0

Tätä käytetään, koska yhtälö, jonka aste on suurempi kuin kaksi, on seurausta polynomin tekijästä; toisin sanoen se ilmaistaan ​​yhden tai suurempien polynomien kertolasku, mutta ilman todellisia juuria.

Tämän tyyppisten yhtälöiden ratkaisu on suora, koska kahden tekijän kertominen on yhtä suuri kuin nolla, jos jokin tekijä on nolla (0); Siksi jokainen löydetty polynomiyhtälö on ratkaistava, sovittaen jokainen sen tekijä nollaan.

Esimerkiksi, sinulla on kolmannen asteen yhtälö (kuutio) x³ + x² +4x + 4 = 0. Sen ratkaisemiseksi sinun on noudatettava seuraavia vaiheita:

• Ehdot on ryhmitelty:

x³ + x² +4x + 4 = 0

(x³ + x² ) + (4x + 4) = 0.

• Jäsenet hajoavat saadakseen tuntemattoman yleisen tekijän:

x² (x + 1) + 4 (x + 1) = 0

(x² + 4)_*(x + 1) = 0.

• Tällä tavoin saadaan kaksi tekijää, joiden on oltava yhtä suuri kuin nolla:

(x² + 4) = 0

(x + 1) = 0.

• Voidaan nähdä, että tekijä (x² + 4) = 0: lla ei ole todellista ratkaisua, kun taas tekijä (x + 1) = 0 kyllä. Siksi ratkaisu on:

(x + 1) = 0

x = -1.

Ratkaisut

Ratkaise seuraavat yhtälöt:

Ensimmäinen harjoitus

(2x² + 5)_*(X - 3)_*(1 + x) = 0.

Ratkaisu

Tässä tapauksessa yhtälö ilmaistaan ​​polynomien kertolasku; eli se on otettu huomioon. Sen ratkaisemiseksi jokaisen tekijän on oltava yhtä suuri kuin nolla:

2x² + 5 = 0, ei ole ratkaisua.

x - 3 = 0

x = 3.

1 + x = 0

x = - 1.

Tällä tavalla annetulla yhtälöllä on kaksi ratkaisua: x = 3 ja x = -1.

Toinen harjoitus

x⁴ - 36 = 0.

Ratkaisu

Annettiin polynomi, joka voidaan erottaa neliöiden erona nopeamman liuoksen saavuttamiseksi. Siten yhtälö säilyy:

(x² + 6)_*(x² - 6) = 0.

Yhtälöiden ratkaisun löytämiseksi molemmat tekijät ovat yhtä suuret kuin nolla:

(x² + 6) = 0, ei ole ratkaisua.

(x² - 6) = 0

x² = 6

x = ± √6.

Siten alkuperäisessä yhtälössä on kaksi ratkaisua:

x = √6.

x = - √6.