Ellipsoidiset ominaisuudet ja esimerkit

Hän ellipsoidi Se on pinta avaruudessa, joka kuuluu nelikorvaisten pintojen ryhmään ja jonka yleinen yhtälö on muodoltaan:

Kirves² + Ohella² + Cz² + Dxy + exz + fyz + gx + hy + iz + j = 0

Se on ellipsin kolmiulotteinen ekvivalentti, jolle on ominaista elliptiset ja pyöreät jäljet ​​joissain erityistapauksissa. Jälkit ovat käyrät, jotka saadaan leikkaamalla ellipsoidia tason kanssa.

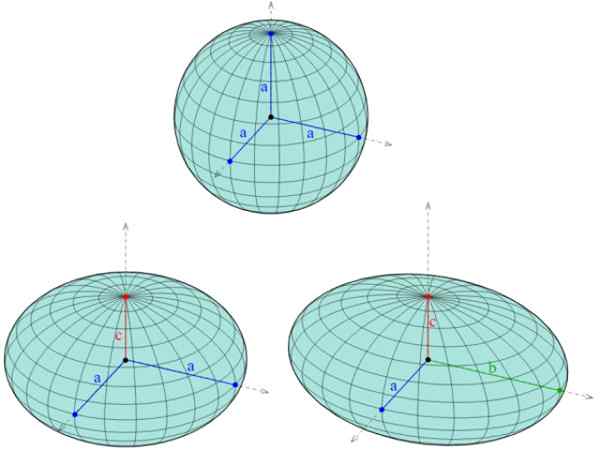
Kuvio 1. Kolme erilaista ellipsoidia: pallon yläpuolella, jossa kolme puoli -semi ovat samat, vasemmalle asti, sferoidi, kahdella yhtä suurella puolikerroksella -yksi -akselilla ja lopulta oikealle, triaksiaalinen sferoidi, kolmella akselilla, kolmella akselilla eri pituus. Lähde: Wikimedia Commons. Ag2gaeh/cc by-s (https: // creativecommons.Org/lisenssit/by-SA/4.0)

Ellipsoidin lisäksi on viisi muuta nelikirjaa: yhden lehden hyperboloidi ja kaksi lehtiä, kaksi tyyppiä paraboloidia (hyperbolinen ja elliptinen) ja elliptinen kartio. Hänen jäljet ​​ovat myös kartiomaisia.

Ellipsoidi voidaan ilmaista myös vakioyhtälöllä Cartesian koordinaateissa. Alkuperäiseen (0,0,0) keskittyvä ellipsoidi ja tällä tavalla ilmaistu, muistuttaa ellipsia, mutta ylimääräisellä termillä:

Arvot -lla, b - ja c Ne ovat todellisia lukuja suurempia kuin 0 ja edustavat kolmea ellipsoidia puolta.

[TOC]

Ellipsoidiset ominaisuudet

- Vakioyhtälö 

Kartesian koordinaattien vakioyhtälö ellipsin keskittyminen kohtaan (H, K, M) On:

- Ellipsoidiset parametriset yhtälöt

Pallomaisissa koordinaateissa ellipsoidia voidaan kuvata seuraavasti:

x = sin θ. cos φ

y = b sin θ. synti φ

Z = c cos θ

Ellipsoid -puoliksi -out ovat edelleen A, B ja C, kun taas parametrit ovat seuraavan kuvan kulmat θ ja φ:

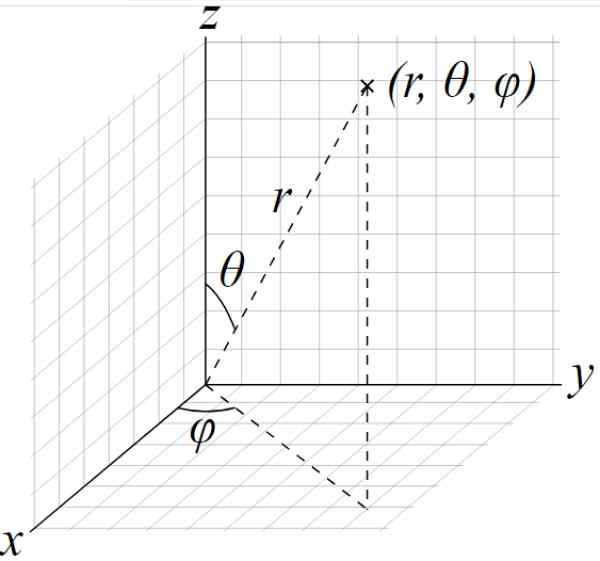Kuva 2. Pallomainen koordinaattijärjestelmä. Ellipsoidi voidaan parametroida käyttämällä parametreina esitetyt kulmat ja phi. Lähde: Wikimedia Commons. Andeggs / Pub -verkkotunnus.

- Ellipsoidiset jäljet

Pinnan yleinen yhtälö avaruudessa on F (x, y, z) = 0 ja pinnan jäljet ​​ovat käyrät:

Voi palvella sinua: vektorisuuntaus

- x = c; F (c, y, z) = 0

- y = c; F (x, c, z) = 0

- Z = c; F (x, y, c) = 0

Ellipsoidin tapauksessa tällaiset käyrät ovat ellipsejä ja joskus kehysiä.

- Tilavuus

Ellipsoidin tilavuus V annetaan (4/3) π -kertaa sen kolmen puolikerin tuote:

V = (4/3) π. ABC

Erityiset ellipsoiditapaukset

-Ellipsoidista tulee pallo, kun kaikki puoliksi kokoiset ovat samankokoisia: a = b = c ≠ 0. Tämä on järkevää, koska ellipsoidi on kuin pallo, johon se on venytetty eri tavalla jokaisella akselilla.

-Sfheroid.

Sferoidia kutsutaan myös vallankumoukseksi ellipsoidiksi, koska se voidaan luoda kiertämällä ellipsit akselin ympärillä.

Jos kääntöakseli osuu pääakseliin, sferoidi on tulkija, Mutta jos se osuu samanaikaisesti pienen akselin kanssa, se on navoilta litistynyt-

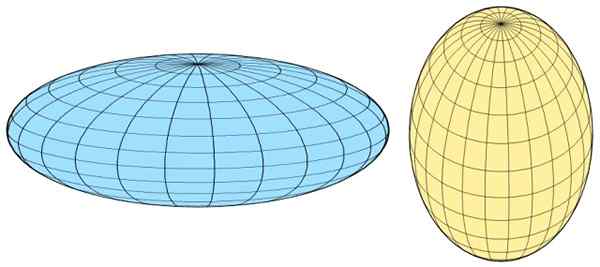Kuva 3. Sferoid. Lähde: Wikimedia Commons.

Sferoidin tasoittamisen mitta (elliptisyys) annetaan kahden puoliväli -sivun pituuseron perusteella, joka ilmaistaan ​​murto -muodossa, ts. Se on yksikön tasoitus, jonka annetaan:

F = (a - b) / a

Tässä yhtälössä A edustaa puoliksi -senije ja B -vähäistä puoli -akselia, muista, että kolmas akseli on yhtä suuri kuin mikä tahansa näistä spheroidille. F: n arvo on välillä 0 ja 1 ja pallomoidelle sen on oltava suurempi kuin 0 (jos se olisi yhtä suuri kuin 0, meillä olisi yksinkertaisesti pallo).

Voi palvella sinua: Bethelgeuse

Referenssi ellipsoidi

Planeetat ja yleensä tähdet eivät yleensä ole täydellisiä palloja, koska kiertoliike akseliensa ympärillä on vartaloa ja bassiinit Ecuadorissa.

Siksi maa näyttää olevan kuin oblate Sfheroid, vaikkakaan ei niin liioiteltu kuin edellisen hahmon, ja toisaalta kaasumainen Saturn -jättiläinen on katkera aurinkojärjestelmän planeettoja.

Joten realistisempi tapa edustaa planeettoja on olettaa, että ne ovat kuin vallankumouksen pallot tai ellipsoidi, jonka puoliksi -Semi -Major on päiväntasaajan radio ja pieni puoliksi -akseli polaarisäde.

Maapallolla tehdyt huolelliset toimenpiteet ovat antaneet rakentaa Viite ellipsoidi maapallon tarkka muoto toimia matemaattisesti.

Tähteillä on myös kiertoliikkeitä, jotka antavat heille enemmän tai vähemmän litistettyjä muotoja. Eridanuksen eteläisen tähdistössä oleva nopea aternar -tähti, kahdeksas kirkkain tähti yötaivaalla, on huomattavan elliptinen vertaamalla sitä enemmistöön. Se on 144 valovuotta meistä.

Toisessa ääripäässä muutama vuosi sitten tutkijat antoivat tähän mennessä löydetyn pallomaisimman esineen: Kepler 11145123 -tähti, 5000 valovuotta, koko on kaksinkertainen aurinko ja ero vain 3 km: n puolijohtojen välillä, vain 3 km. Odotetusti se kääntyy myös hitaammin.

Maapallon suhteen se ei ole täydellinen spheroidi sen karkean pinnan ja paikallisten painovoiman variaatioiden takia. Siksi on enemmän kuin yksi käytettävissä oleva referenssipaferoidi ja jokaisella paikalla on valitaan sopivin paikalliselle maantieteelle.

Se voi palvella sinua: mikä on fysiikan laakso? (Esimerkkejä)

Satelliittien apu on arvokasta luomalla yhä tarkempia malleja maanmuotoisia malleja, niiden ansiosta tiedetään esimerkiksi, että etelänapa on lähempänä Ecuadoria kuin pohjoisnapa.

Kuva 4. Haumea, Transneptunian kääpiöplaneetalla on ellipsoidinen muoto. Lähde: Wikimedia Commons.

Numeerinen esimerkki

Maan pyörimisen vuoksi syntyy keskipakoisvoima, joka antaa sille pitkänomaisen ellipsoidin muodon pallon sijasta. On tiedossa, että maan päiväntasaajan radio on 3963 mailia ja polaarinen säde on 3942 mailia.

Löydä päiväntasaajan jäljen yhtälö, tämän ellipsoidin yhtälö ja sen litistuksen mitta. Vertaa myös Saturnuksen elliptisyyteen, alla oleviin tietoihin:

-Saturnuksen päiväntasaajan radio: 60268 km

-Saturn Polar Radio: 54364 km

Ratkaisu

Vaaditaan koordinaattijärjestelmä, jonka oletetaan keskittyvän alkuperään (maan keskustaan). Oletetaan, että pystysuora z -akseli ja päiväntasaajaa vastaava jälki on XY -tasossa, vastaavat tasoa z = 0.

Päiväntasaajan tasossa puoliksi -a ja b ovat samat, joten a = b = 3963 mailia, kun taas c = 3942 mailia. Tämä on erityistapaus: pisteen (0,0,0) keskittynyt pallot, kuten yllä todettiin.

Päiväntasaajan jälki on säteen R = 3963 mailin ympyrä, joka keskittyy alkuperään. Se lasketaan tekemällä z = 0 vakioyhtälössä:

Ja maapallon ellipsoidin vakioyhtälö on:

Lopuksi säätömitta (elliptinen) lasketaan arvioimalla yhtälössä:

F _Maa = (a - b) / a = (3963-3942) mailia / 3963 mailia = 0.0053

F _Saturnus = (60268-54363) km/60268 km = 0.0980

Huomaa, että elliptinen F on mitoiton määrä.

Viitteet

1. Työpöydän arcgis. Pallot ja pallot. Palautettu: Työpöytä.Kaari.com.
2. BBC -maailma. Maailmankaikkeudesta koskaan löydetyn pallomaisen esineen mysteeri. Haettu osoitteesta: BBC.com.
3. Larson, r. Laskenta ja analyyttinen geometria. Kuudes painos. Nide 2. McGraw Hill.
4. Wikipedia. Ellipsooid. Haettu: vuonna.Wikipedia.org.
5. Wikipedia. Siperoidi. Haettu: vuonna.Wikipedia.org.