Mitkä tilanteet ovat lineaarisia ja neliömäisiä funktioita?

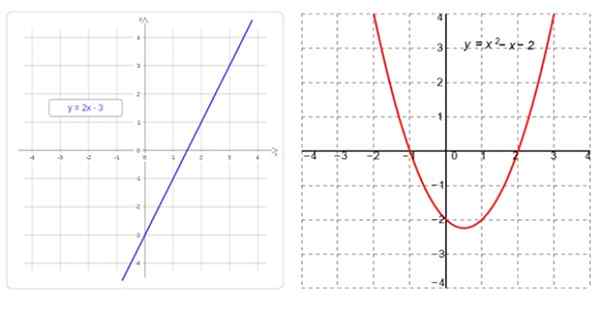
Vasemmalle lineaarinen funktio, jonka kaavio on suora ja oikealla puolella, neliöfunktio, jonka kuvaaja on parabola. Lähde: f. Zapata

Mitkä ovat lineaariset ja neliölliset toiminnot?

Lineaariset funktiot ja neliömäiset funktiot ovat toimintoja, jotka kuuluvat polynomisiin funktioihin. Niitä käytetään mallintamaan erilaisia ​​tilanteita, kuten kehon tilavuuden ja painon, tuotteen määrä ja kustannukset, sijainti verrattu.

Yleensä funktio on suhde, joka yhdistää kaksi muuttujaa ja jota voidaan käyttää todellisen maailman mallintamiseen. Polynomiset funktiot, kuten nimestä päätetään, ilmaistaan ​​polynomin kautta, jonka yleinen muoto on:

f (x) = a_nxⁿ + -lla _N-1x ^N-1 + -lla_X-2x^N-2 +…_jompikumpi

Missä n on luonnollinen luku, numerot_{0 -}, -lla₁, -lla₂,…_n Ne ovat todellisia,_{0 -} Se on riippumaton termi ja_n, Korkeimman voiman mukana on kerroin. N: n arvo osoittaa funktiotyypin, funktiossa n = 1 on lineaarinen, kun taas n = 2 funktio on neliömäinen.

Ensimmäisessä näistä tapauksista yleinen lauseke pelkistetään:

f (x) = a₁x + a_jompikumpi

Ja toisessa tapauksessa se pysyy näin:

f (x) = a₂x² + -lla₁x + a_jompikumpi ;   (₂≠ 0)

Polynomifunktioiden kaaviot ovat jatkuvia, ts. Ne eivät koe äkillisiä hyppyjä tai repeämiä, joten sillä on pehmeä käyttäytyminen ilman väärinkäytöksiä. Siksi niitä havaitaan monien tieteen, taloustieteen ja muiden ihmisten tietämyksen alueille mallinnuksessa.

Seuraavaksi mielenkiintoisia sovelluksia on kuvattu yksityiskohtaisemmin.

Tilanteet, joissa lineaariset toiminnot ilmestyvät

Lineaarista funktiota edustaa algebrallisesti:

f (x) = a₁x + a_jompikumpi

Tai vastaavasti:

f (x) = mx + b

Sen erottuva ominaisuus on, että sen kaavio on suora. Arvo m, mikä on kerroin x, edustaa korvarengas tästä linjasta ja antaa mittaan kuinka taipuvainen se on.

Voi palvella sinua: epälineaarinen ohjelmointi: menetelmät ja harjoitukset

Kaltevuus voi olla positiivinen, negatiivinen tai nolla, mutta se on aina vakio, toisin sanoen sen valuuttakurssi pysyy muuttumattomana.

Kaltevuuslinja 0 on täysin vaakasuora, positiivisen kaltevuuden linja osoittaa korkeuden tai nousun (jos jokin muuttujista kasvaa, toinen myös, aina samalla nopeudella) ja lopuksi negatiivinen kaltevuus osoittaa laskun (muuttujien A: na kasvaa, toinen vähenee).

Arvo b -, Se puolestaan ​​edustaa viivan leikkausta tai leikkausta pystysuoran akselin kanssa. Joo B = 0, Linja kulkee koordinaattijärjestelmän alkuperän.

Esimerkkejä lineaarisilla funktioilla

1. Tasainen suorakulmainen liike

Yhtälö, joka yhdistää matkapuhelimen X -aseman ja ajan T: n tasaisessa suorakulmaisessa liikkeessä, on lineaarinen:

x (t) = v⋅t + x_jompikumpi

Missä V, linjan kaltevuus, on matkapuhelimen nopeus, joka pysyy vakiona koko liikkeen ajan, ja x_jompikumpi on alkupaikka.

2. Tiheys

Esineen tai aineen tiheys, joka luo massa- ja tilavuuden välisen suhteen. Soittamalla ρ tiheyteen (se lukee "Rho"), M taikinaan ja V: lle, sinulla on:

Taikinan tyhjentäminen tilavuuden suhteen se saadaan:

M = ρv

Kun taikina kuvaa tilavuudesta riippuen, saadaan suora viiva, jonka kaltevuus on esineen tai aineen tiheys.

3. Kehän pituus

Ympyrän tai sen pituuden muoto on verrannollinen sen säteeseen. Tämä tarkoittaa, että mitä suurempi säde on, sitä suurempi on ympärysmitta yhtälön mukaan:

Voi palvella sinua: Korrelaatiokerroin: kaavat, laskenta, tulkinta, esimerkki

C = 2πr

Jos C on ääriviivat tai pituus, r on radio ja π (lukee ”pi”) on vakio, jonka likimääräinen arvo on πamp3.14 ..

4. Paketin lähettämisen kustannukset

Koska se on helppo päätellä, raskaampi tai tilaa vievä on kalliimpi paketti on kuljettaa sitä. Yritykset, jotka ovat omistettu lastin kuljetusmalliin, esimerkiksi tiettyjen sääntöjen mukaiset hinnat:

C (x) = 2.75x

Tässä yhtälössä c (x) on dollarin kustannus paketin lähettämiseen, jonka paino on x kiloa. Vakioarvo 2.75: llä on yksiköitä dollaria/punta (yksikkökustannukset).

Tilanteet, joissa neliömäiset toiminnot ilmestyvät

Algebrallisesti neliömäistä funktiota edustaa:

f (x) = a₂ x² + -lla₁ x + a_jompikumpi

Sillä ehdolla, jonka kertoimet₂ Olla erilainen kuin 0. Sille on ominaista sen parabola -muotoinen kuvaaja, jonka aksiaalinen akseli tai symmetria -akseli on pystysuuntainen (yhdensuuntainen Y -akselin kanssa)).

Parabuelin ja mainitun akselin välinen risteys on piste nimeltään Vertex. Jos vertaus avautuu (a₂ > 0), kärki on sen vähimmäispiste, ja jos se avautuu (a₂ < 0), es el máximo.

Symmetrian akselilla on tarkennus, erityinen kohta, joka määrittää parabolin kaarevuuden. Jos auringonvalo vaikuttaa paraboliseen peiliin, säteet heijastuvat pinnalle, samoin kuin tarkennus, joka lämmitetään välittömästi.

Esimerkkejä neliömäisillä toiminnoilla

1. Ammuksen korkeus käynnistettiin pystysuunnassa

Ammus on mikä tahansa esine, jolle alkuperäinen nopeus tarjotaan ja vapautetaan sitten painovoiman mukaisesti. Jos alkuperäinen nopeus on pystysuora, voimakkuus V_{0 -} ja ohjattu, esine nousee enimmäiskorkeuteen ja laskeutuu sitten.

Voi palvella sinua: Homotecia

Korkeuden H yhtälö ajan funktiona t on:

H (t) = −4.9 t²+v_{0 -} t

Missä pystysuora merkitys pidetään positiivisena ja pystysuora negatiivinen.

2. Vaakasuuntaisen tai vino ammuksen suuntaus

Jos ammukselle annetaan vaakasuora tai vino alkuperäinen nopeus, se kuvaa parabolista etenemissuuntausta, joka voidaan edustaa kvadraattisella funktiolla, kuten aiemmin on kuvattu.

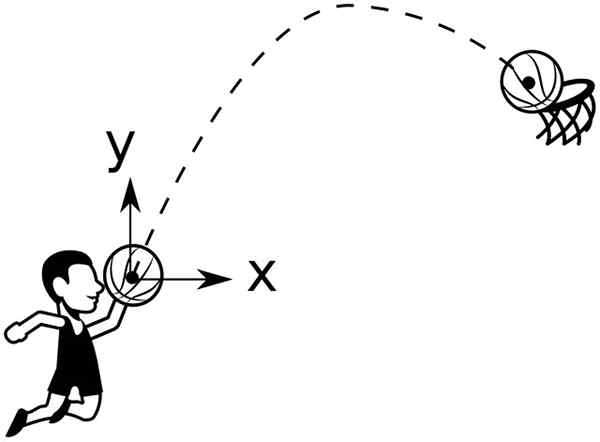Korin pallo kuvaa parabolista etenemissuuntausta, joka heitetään koriin. Lähde: Wikimedia Commons

Esimerkiksi pallo, joka on heitetty korkeudesta ja_{0 -}, Muodostuskulma θ_{0 -} Vaakasuoran suhteen sillä on: Annetaan:

G: n kanssa painovoiman kiihtyvyytenä, joka voi suunnitella 10 m/s². Esimerkiksi jalkapallopallo potkaisee maasta (ja_{0 -} = 0), alkuperäisen nopeuden ollessa 6 m/s ja kulma 45º vaakasuoraan nähden, seuraavan vertauksen antama etenemissuunta:

3. Ympyrän alue

Mitä korkeampi ympyrän säde, sitä suurempi sen pinta -ala on. Itse asiassa ympyrän pinta -ala on verrannollinen säteen R neliöön, suhteellisuusvakio on luku π:

A = πr²

4. Mainoksen tehokkuus

Mitä enemmän he näkevät sen, sitä tehokkaampi kaupallinen mainos. Tehokkuus E, asteikolla 0 - 10, yhdestä ilmoituksesta voidaan mallintaa seuraavan neliömäisen toiminnon mukaisesti:

Viitteet 

1. Polynomiset funktiot. Palautettu resursseista.koulutus.On.
2. Larson, r. (2012). Ennakkoluulo. Kahdeksas. painos. Cengage -oppiminen.
3. Miller, c. (2013). Matematiikka: päättely ja sovellukset. 12. päivä. painos. Pearson -koulutus.
4. Stewart, J. (2012). Ennakkoluulo. Matematiikka laskentaa varten. Kuudes. painos. Cengage -oppiminen.
5. Zill, D. (2008). Ennakkoluulo laskenta etenee. Neljäs. painos. McGraw Hill.