Pakkauskerroin

Pakkauskerroin on murto, joka osoittaa, kuinka paljon tilavuutta hiukkaset miehittävät, olipa atomeja, ioneja tai molekyylejä, kideen sisätilassa. Sen arvo on aina alle 1, josta tulee 100% lasin tilavuudesta; Tarkemmin sanottuna sen yhtenäinen solu, joka on koko lasin pienin esitys.

100% pakkauskerroin tarkoittaa, että hiukkaset miehittävät yhtenäisen solun tilavuuden kokonaisuudessaan. Fyysisesti on mahdotonta, että tämä tapahtuu, koska se merkitsisi esimerkiksi, että atomit muodostuvat radioistaan ​​ja liukenevat ikään kuin ne olisivat "elektronisia nesteitä". Atomien geometria, pallomainen mukavuuden suhteen, johtaa aina tyhjiin tiloihin pakkauksen aikana.

Kuten makeissa annostelukoneissa tapahtuu, pakkauskerroin kertoo meille, kuinka ”tiukat” ovat kide hiukkaset: mitä suurempi se on, sitä enemmän kumia tai atomeja, avaruudessa on

Pakkauskertoimen määritelmässä oletetaan, että atomit koostuvat jäykistä palloista, kuten annostetun koneen kumi tai karkkipallot (ylivoimainen kuva). Alueista on aina onttoja tiloja, joissa pienemmät pallot (epäpuhtaudet tai lisäaineet voidaan hiipiä).

Jos lisäämme pakkauskerrointa, pallot puristetaan, kääntäen kompakti ja tihein lasi; tai toisaalta, muodonmuutos, kuten muokattavissa ja painavametallissa.

Pakkauskerroin koskee minkä tahansa tyyppisiä laseja. Sen laskelmasta voi kuitenkin tulla vähän tylsää, joten sitä harkitaan vain atomikiteissä, joissa on yksinkertaisia ​​rakenteita.

[TOC]

Pakkauskerroin kaava

Pakkauskerroin ilmaistaan ​​yleensä prosentteina. Esimerkiksi, jos sen arvo on 40%, se tarkoittaa, että hiukkaset tuskin miehittävät 40% yksikkösolun kokonaistilasta; tai mikä on sama kuin väittää, että 60% lasista on "tyhjä".

Yllä oleva selventää, mikä on kaava tämän tekijän laskemiseksi:

• Ruma = (atomien tilavuus)/ (yksikkösolujen tilavuus)

Missä ruma tarkoittaa Atomipakkauskerroin, Mitkä ovat yksinkertaisimmat kiteet.

Yksikkösolun tilavuus riippuu sen parametreista (kuten sivujen pituudesta), jonka kanssa se etenee yksinkertaisella geometrialla sen tilavuuden laskemiseksi. Atomit puolestaan ​​ovat niitä, jotka määrittelevät solun, joten on mahdollista ilmaista saman mitat atomiradioista, kuten seuraavissa osissa nähdään.

Se voi palvella sinua: Racemic Mix: kiraalisuus, esimerkit

Atomien tilavuuden suhteen niiden kokonaismäärä, jota on yksikkösolussa (1, 2, 3, jne.), samoin kuin pallomainen geometria. Siksi kaavaa on muokattu hiukan:

Ugly = (nº -atomit) (atomitilavuus)/ (yksikkösolujen tilavuus)

Ruman laskemiseksi sinun on määritettävä sitten nro, v_atomi ja v_{Yhtenäinen solu}.

Yksinkertainen kuutio

Yksinkertainen kuutioyksikkösolu. Lähde: CCC_Crystal_Cell_ (läpinäkymätön).Svg: *cobique_centre_atomes_par_maille.SVG: CDANG (alkuperäinen idea ja SVG-toteutus), Samuel Dupré (3d Odeeling with SolidWorks).0, Wikimedia Commons

Kaikkien yksinkertaisin yhtenäinen solu on yksinkertainen kuutio. Siinä on joitain atomeja jokaisessa kulmassa. Jos näemme, huomaamme sen pituuden -lla Tästä solusta se on yhtä suuri kuin 2R, koska solun määrittelevät atomit. Joten yksikkösolun tilavuus on yhtä suuri kuin:

V_{Yhtenäinen solu} = -lla³ (kuution tilavuus)

= (2R)³

= 8R³

Samaan aikaan atomin tilavuus on yhtä suuri kuin:

V_atomi = (4/3) πr³ (pallon tilavuus)

Jokainen kulma jakavat vielä 8 vierekkäistä yksikkösolua. Siksi meillä on 1/8 fraktiossa jokaisessa nurkassa, ja niistä 8, emme välitä 1 atomi solua kohti (1/8 x 8 = 1).

Pakkauskerroin on:

Ruma = (1) (4/3) πr³ /8R³

= π/6 ≈ 52%

Eli yksinkertaisessa kuutiosolussa atomit miehittävät 52% koko lasitilavuudesta.

Kuutiokeskeinen kehoon

Solutilavuuden määrittäminen

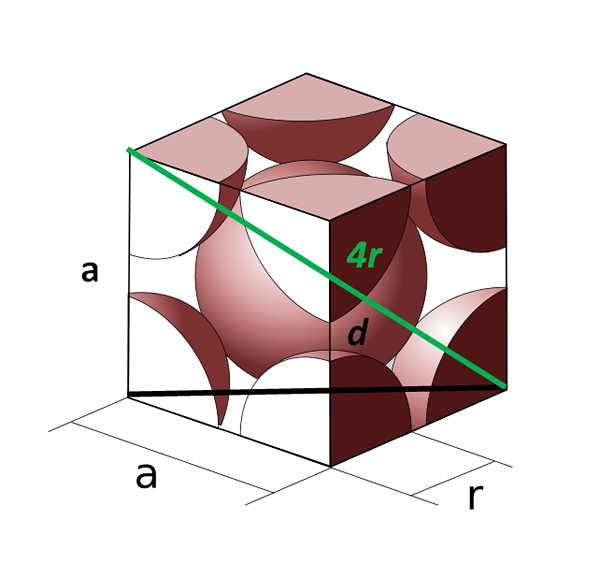Kehon yhtenäinen solu keskittyy vartaloon. Lähde: Cobque_centre_atomes_par_maille.SVG: CDang (alkuperäinen idea ja SVG-toteutus), Samuel Dupré (3d Odeeling kanssa SolidWorks) johdannainen työ: Daniele Pugliesi, CC BY-SA 3.0, Wikimedia Commons

Katsotaanpa nyt kehoon keskittyvä kuutiosolu. Puoli -lla Se ei voi enää olla yhtä suuri kuin 2R, koska meillä on tyhjä tila kulmien kahden atomin välillä. Siksi on diagonaali d -d yhtä suuri kuin 4R (vihreä väri), joka ylittää solun keskustan läpi ja koskettaa vastakkaisia ​​kulmia ja toinen diagonaali d -d kasvot (musta).

Sivut -lla, d -d ja 4R piirrä suorakulmiokolmio, johon voimme käyttää trigonometriaa laskeaksesi mikä on -lla-

(4R)² = D² + -lla²

Voi palvella sinua: molekyylien väliset voimat

Mutta toisaalta, yksikkösolun pohjassa meillä on toinen kolmio (-lla, -lla ja d -d) johon voimme laskea hypotenusen:

d -d²  = a² + -lla²

= 2a²

Korvataan sitten: Meillä on:

(4R)² = (Toinen²) + a²

(4R)² = 3a²

A = (4/√3) r

V_{Yhtenäinen solu} on yhtä suuri kuin:

V_{Yhtenäinen solu} = a³

= ((4/√3) r)³

Pakkauskertoimen määrittäminen

Huomaa, että atomien lukumäärän suhteen meillä on yksi atomi tämän solun sisällä, seuraavan yksinkertaisen kuutiosolun ja toisen ylimääräisen atomin seurauksena, joka sijaitsee solun keskellä. Siten jokaiselle kehoon keskittyvälle kuutiosolulle on yhteensä 2 atomia.

Pakkauskerroin on sitten:

Ruma = (2) (4/3) πr³ / ((4/ √3) r)³

= (√3/8) π ≈ 68%

Toisin sanoen kehossa keskittyvässä kuutiosolussa 68% lasitilavuudesta on atomien miehittämä. Tämän seurauksena tämä kiteinen järjestely on kompakti (tai tiheämpi) kuin yksinkertainen kuutiometriä.

Kuutio keskittyy kasvoihin

Solutilavuuden määrittäminen

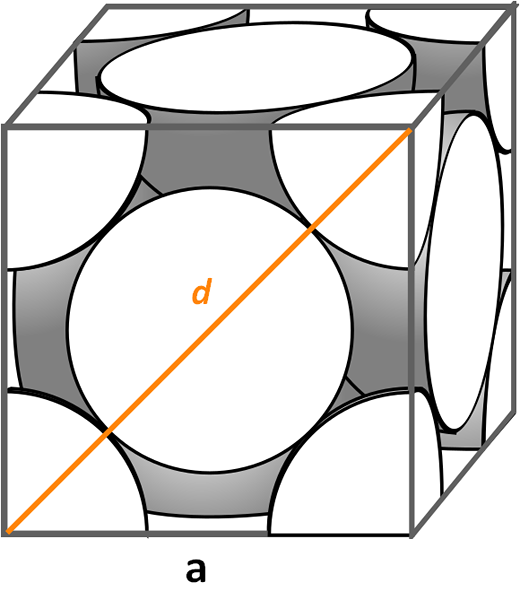Kuubinen yhtenäinen solu, joka on keskittynyt kasvoihin. Lähde: Cdang, CC BY-SA 3.0, Wikimedia Commons

Katsotaanpa kasvoihin keskittyvää kuutiometriä yhtenäistä solua, joka on hyvin yleinen epäorgaanisten suolojen ja joidenkin metallien, kuten kultaa ja hopeaa, sinfiineissä. Sen pakkauskertoimen määrittämiseksi meidän on aloitettava aiempien esimerkkien seuraaminen löytääksemme, mikä sen yksikkösolun tilavuus on. On tarpeen laskea puoli uudelleen -lla Ja niin kuution tilavuus -lla³.

Tällä kertaa toimenpide on helpompaa ja suorempaa, koska meillä on diagonaali d -d Edessä, yhdessä sivujen kanssa -lla, Ne muodostavat oikean kolmion, johon voimme soveltaa trigonometriaa:

d -d² = a² + -lla²

= 2a²

Puhdistus -lla meillä tulee olemaan:

-lla = D/√2

Mutta huomaamme sen visuaalisesti d -d Se on yhtä suuri kuin 4R, joten teemme korvaamisen:

-lla = 4R/√2

= 2R 2^1-1/2

= (2√2) r

Olla V_{Yhtenäinen solu} yhtä kuin:

-lla³ = ((2√2) r)³

= (16√2) r³

Atomien lukumäärän suhteen solua kohti, meillä on kahdeksan osaa yhdestä atomista jokaisessa nurkassa ja myös puolet atomista jokaiselle kuudelle pinnalle, jonka jakavat toinen naapurisolu. Siksi atomien lukumäärä on yhtä suuri kuin:

Nº Atomit = 1/8 (8) + 1/2 (6) = 1 + 3 = 4

Pakkauskertoimen määrittäminen

Kun jokaisessa kuutiosolussa on 4 atomia, jotka keskittyvät kasvoihin, ja myös sen tilavuus, joka on yhtä suuri kuin (16√2) r³, Voimme sitten laskea pakkauskertoimen:

Ugly = (nº -atomit) (atomitilavuus)/ (yksikkösolujen tilavuus)

= (4) (4/3) πr³ / (16√2) r³

Se voi palvella sinua: Acilo -ryhmä: rakenne, ominaisuudet, yhdisteet ja johdannaiset

= π/(3√2) ≈ 74%

Huomaa, että tämä solu on jopa kompakti kuin aikaisemmat: 74% solun kokonaistilavuudesta on atomien miehittämä. Täydellisessä ja puhtaassa kristallissa tämä vastaa sanoen, että 26% sen tilavuudesta on käytettävissä muiden vierasatomien isännöimiseksi.

Kompakti kuusikulmainen

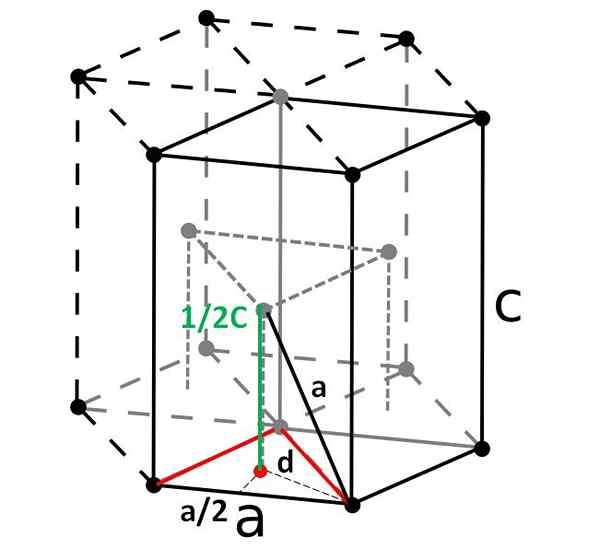Kompakti kuusikulmainen solu ja sen rhomboedrinen primitiivinen solu. Lähde: Alkuperäinen: DornelfVector: DePiep, CC By-Sa 3.0, Wikimedia Commons

Lopuksi, yksinkertaisimpien ja kompaktien yksikkösolujen joukossa meillä on kompakti kuusikulmainen. Toisin kuin aiemmat, sen tilavuuden laskeminen on hieman hankalampi. Kuten voidaan nähdä, se ei ole kuutio, joten siinä on kaksi parametria -lla ja c, Jälkimmäinen on solun korkeus.

Solun korkeuden määrittäminen

Kuusikulmainen solu voidaan jakaa kolmeen rhomboyan -soluun, ja yhdestä heistä se lasketaan -lla ja c. Puoli -lla, Vaikka se ei ole niin ilmeinen yllä olevassa kuvassa, se on yhtä suuri kuin 2R. Laskea c, Sen sijaan käytämme saman solun kolmiota ja punaisen pisteen tuotetta.

Meidän on laskettava etäisyys d -d Voidakseen selvittää, kuinka paljon se on arvoinen c. Lattialla punainen kolmio on tasapaino, kulma 60º. Mutta jos sivuilla otetaan huomioon toinen sisäinen suorakulmiokolmio -lla/2 ja d -d, ja 30º (puoli) kulma, sitten trigonometrialla voimme määrittää d -d-

Cos (30º) = (-lla/2) / d -d

d -d = -lla/√3

Ja nyt tarkastellaan oikeaa kolmiota, joka koostuu sivuista c/2 (vihreä), -lla (musta) ja d -d (Pistetty):

-lla² = (-lla/√3)² + (C/2)²

Puhdistus c Meillä olisi:

c = √ (8/3) -lla

Ja korvaaminen -lla Kirjoittanut 2r:

c = √ (8/3) (2R)

= √ (4 · 2/3) (2r)

= 4√ (2/3) r

Solutilavuuden määrittäminen

Kuusiogonaalisen solun tilavuuden määrittämiseksi sinun on kerrottava kuusikulmioalue sen korkeudella. Tietäen, että tasasivuisilla kolmioilla on puolia -lla, Sen korkeus on laskettu h. Siten kolmion alueen löytäminen, joka on tässä tapauksessa √3/4-lla², Kertomme tämän arvon 6: lla kuusikulmion alueen saamiseksi: 3 (√3/2)-lla²

Volume on siis:

V_{Yhtenäinen solu} = Hexagonin alue x korkeus

= 3 (√3/2)-lla² X 4√ (2/3) r

Ja korvaaminen jälleen kerran -lla Kirjoittanut 2r:

V_{Yhtenäinen solu}  = 3 (√3/2) (2R)² X 4√ (2/3) r

= 24√2 r³

Pakkauskertoimen määrittäminen

Kuusikulmaisessa solussa kulmassa on 12 atomia, joiden tilavuudet ovat 1/6. On myös 3 sisäistä atomia, joiden tilavuudet ovat täydellisiä, ja vielä 2 ylemmässä ja alapuolella olevia atomeja, joiden puolet sen tilavuuksista on solun sisällä.

Siksi atomien lukumäärä on yhtä suuri kuin:

Nº -atomi = 1/6 (12) + 1 (3) + 1/2 (2) = 6 atomia

Ja pakkauskerroin on vihdoin:

Ugly = (nº -atomit) (atomitilavuus)/ (yksikkösolujen tilavuus)

= (6) (4/3) πr³ / 24√2 r³

= π/(3√2) ≈ 74%

Huomaa, että kuusikulmaisen solun osastokerroin on sama kuin kuutiosoluun, joka on keskittynyt kasvoihin. Toisin sanoen molemmat ovat yhtä kompakteja.

Viitteet

1. C. Barry Carter & M. Grant Norton. (2007). Keraamiset materiaalitieteet ja tekniikka. Jousto.
2. Shiver & Atkins. (2008). Epäorgaaninen kemia. (Neljäs painos). MC Graw Hill.
3. Whitten, Davis, Peck & Stanley. (2008). Kemia. (8. ed.-A. Cengage -oppiminen.
4. Wikipedia. (2021). Atomipakkauskerroin. Haettu: vuonna.Wikipedia.org
5. Brandon. (2021). Mikä on atomipakkauskerroin (ja kuinka laskea se SC: lle, BCC: lle, FCC: lle ja HCP: lle)? Materiaalitieteen ja tekniikan opiskelija. Toipunut: MsESTUDENT.com