Viskoosinen kitka (voima) -kerroin ja esimerkit

Se viskoosinen kitka Se syntyy, kun kiinteä esine liikkuu neste -un -kaasun tai nesteen keskellä-. Se voidaan mallintaa voimana, joka on verrannollinen esineen tai neliön nopeuden negatiiviseen.

Yhden tai toisen mallin käyttö riippuu tietyistä olosuhteista, kuten nesteen tyypistä, jossa esine siirretään ja onko se kovin nopea. Ensimmäinen malli tunnetaan nimellä Lineaarinen vastus, ja siinä viskoosisen kitkan suuruus f_kosketus Se on annettu:

F_kosketus = Γv

Kuvio 1. Paracharidistit kokevat viskoosisen voiman laskeutumisensa aikana, koska Air tarjoaa vastustuskykyä. Lähde: Pixabay.

Tässä γ on viskoosisen kitkan suhteellisuus- tai kerroinvakio ja v on esineen nopeus. Sitä sovelletaan runkoihin, jotka liikkuvat alhaisella nesteenopeudella laminaarihuoneistolla.

Toisessa mallissa, joka tunnetaan nimellä Neliömäinen vastus o Rayleightin laki, kitkavoiman suuruus lasketaan:

F_kosketus = ½ ρ.-Lla.C_{d -d}.v²

Jos ρ on nesteen tiheys, A on esineen ristikkäinen alue ja c_{d -d} Se on aerodynaaminen resistenssikerroin.

Tuote ½ ρ.-Lla.C_{d -d}  Se on jatkuva aerodynamiikka, nimeltään D, jonka yksiköt ovat kg/m, siksi:

F_kosketus = DV²

Tämä malli on tarkoituksenmukaisempi, kun esineiden nopeus on keskipitkä tai korkea, koska liike tuottaa turbulenssia tai pyörii polulla nesteessä.

Liikkuva tennispallo ja moottoritien autot ovat esimerkkejä esineistä, joissa tämä malli toimii melko hyvin.

Viskoosivoima syntyy, koska kiinteän aineen on otettava nestekerrokset liikkumaan sen läpi. Useiden mallien olemassaolo johtuu siitä, että tämä voima riippuu useista tekijöistä, kuten nesteen viskositeetista, esineen nopeudesta ja muodosta.

Voi palvella sinua: mikä on suhteellisen läpäisevyys?

Aerodynaamisia esineitä on enemmän kuin muut, ja monet on suunniteltu tarkalleen niin, että keskikeskuksen vastus vähentää sen nopeutta minimiin.

[TOC]

Esimerkkejä viskoosin kitkasta

Jokainen henkilö tai esine, joka liikkuu nesteessä, kokee välttämättä ympäristön vastustuskyvyn, mutta monta kertaa nämä vaikutukset halveksitaan yksinkertaisiin sovelluksiin, kuten vapaa putoaminen.

Lähes kaikkien vapaiden pudotusongelmien lausunnoissa on huomattava, että ilmankestävyyden vaikutukset halveksivat itseään. Tämä johtuu siitä, että ilma on melko "ohut" neste, ja siksi toivomme, että sen kitka ei ole merkittävä.

Mutta on myös muita liikkeitä, joissa viskoosisella kitkalla on ratkaisevampi vaikutus, katsotaanpa joitain esimerkkejä:

Kivet, jotka putoavat veteen ja siitepölyjyviin

-Kallio, joka putoaa pystysuunnassa putkeen, joka on täynnä öljyä, kokee voiman, joka vastustaa sen laskeutumista nestevastuksen ansiosta.

-Siitepölyjyvät ovat hyvin pieniä, joten heille ilman vastus ei ole merkityksetön, koska tämän voiman ansiosta he onnistuvat pysymään pitkään pinnalla, aiheuttaen kausiluonteisia allergioita.

Kuva 2. Siitepölyjyvät ovat riittävän pieniä ilmankestämään merkitsevä vaikutus. Lähde: Pikrepo.

Uimarit ja pyöräilijät

-Uimareiden tapauksessa he käyttävät hattua ja ajellaan kokonaan niin, että veden vastus ei vähennä nopeutta.

-Kuten uimarit, myös pyöräilijöillä, jotka ovat vastarelojissa, ilmankestävyyttä, kypärät ovat aerodynaamisia malleja tehokkuuden parantamiseksi.

Myös pyöräilijän asema ryhmässä kilpailussa on merkityksellinen. Se, joka johtaa marssiin.

Se voi palvella sinua: Toinen tasapainotila: Selitys, esimerkit, harjoitukset

Parakaridistit

-Kun laskuvarjohyppääjä avaa laskuvarjo, se altistetaan ilman viskoosiselle kitkalle, joka on sopivin malli, jolla on nopeuden neliö. Tällä tavoin se vähentää nopeuttaan ja kun hankaaminen on laskua, se saavuttaa vakion raja -arvon.

Auto

-Autoille aerodynaaminen vastuskerroin, vakio, joka määritetään kokeellisesti ja pinta, jota se edustaa tuulta, ovat määrittäviä tekijöitä ilmankestävyyden vähentämiseksi ja kulutuksen vähentämiseksi. Siksi ne on suunniteltu kaltevilla tuulilasilla.

Millikanin öljypisarakoe

-Millikanin öljyn pudotuskokeessa fyysikko Robert Millikan tutki öljypisaroiden liikkumista tasaisen sähkökentän keskellä, päätteli, että mikä tahansa sähkövaraus on elektronikuormituksen moninkertainen.

Tätä varten oli tarpeen tietää tippojen säde, jota ei voitu määrittää suoralla mittauksella, ottaen huomioon sen pieni koko. Mutta tässä tapauksessa viskoosinen kitka oli merkittävä ja pudotukset päätyivät jarrutukseen. Tämä tosiasia antoi määrittää tippojen säteen ja sitten sen sähkövarauksen.

Harjoitukset

- Harjoitus 1

Viskoosisen kitkavoiman yhtälössä alhaisella nopeudella:

F_kosketus = Γv

a) Mitä mittoja viskoosisella kitkakertoimella olisi γ?

b) Mitkä ovat γ -yksiköt kansainvälisessä yksikköjärjestelmässä?

Liittää jhk

Toisin kuin staattiset tai kineettiset kitkakertoimet, viskoosisella kitkakertoimella on mitat, joiden on oltava:

Voi palvella sinua: fyysinen tarttuvuus: Mikä on ja esimerkkejä

Vahvuus / nopeus

Voimalla on massan x pituus /ajan mitat², Vaikka nopeudet ovat pituisia/aikaa. Merkitsemällä heidät seuraavasti:

-Massa: M

-Pituus: l

-Aika: t

Viskoosisen kitkakerroimen γ mitat ovat:

[M.L /t²] / [L / t] = [m.Lens.T / l.T²] = M/t

Ratkaisu b

SI: ssä γ -yksiköt ovat kg/s

- Harjoitus 2

Veden vastustaman vastustuskyvyn huomioon ottaminen etsii ilmaisua metallipaferiitin terminaalisesta nopeudesta, joka putoaa pystysuoraan putkeen, joka on täynnä öljyä, tapauksissa:

a) pieni nopeus

b) nopea

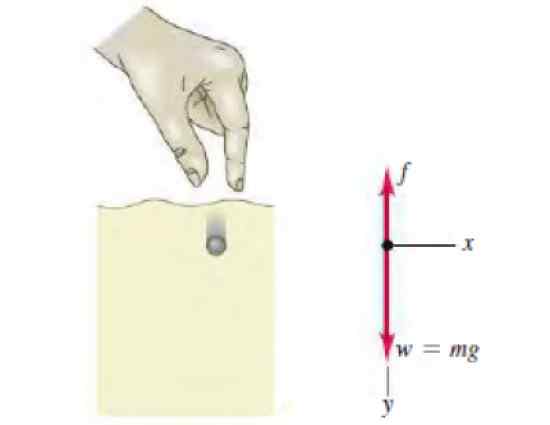Kuva 3. Vapaa runkokaavio pallosta, joka laskeutuu nesteen sisällä. Lähde: Sears, Z. Yliopiston fysiikka, jolla on moderni fysiikka.

Liittää jhk

Kuvassa näkyy vapaa kehon kaavio, joka näyttää kaksi palloilleen vaikuttavaa voimaa: paino ja nesteen vastus, verrannollinen nopeuteen ylöspäin, ylöspäin. Newtonin toinen tämän liikkeen laki vahvistaa seuraavan:

γv_t - Mg = 0

Missä v_t Se on päätelaitteen nopeus, jonka antaa:

v_t = mg / y

Ratkaisu b

Jos oletamme keskimäärin suurilla nopeuksilla, sopiva malli on neliömäinen: neliömäinen nopeus:

F_kosketus = ½ ρ.-Lla.C_{d -d}.v²

Niin:

½ ρ.-Lla.C_{d -d}.v² - Mg = 0

D -d.v² - Mg = 0

v = √ [mg / d]

Molemmissa tilanteissa, mitä suurempi esineen massa, sitä suurempi sen päätenopeus on.

Viitteet

1. Serway, R., Jewett, J. (2008). Fysiikka tieteen ja tekniikan fysiikka. Osa 1. Seitsemäs. Ed. Cengage -oppiminen.
2. Sears, Zemansky. 2016. Yliopiston fysiikka, jolla on moderni fysiikka. 14. päivä. Ed. Osa 1.
3. Tipler, P. (2006) Tieteen ja tekniikan fysiikka. 5. ed. Osa 1. Toimitus palautti.
4. Tippens, P. 2011. Fysiikka: Käsitteet ja sovellukset. 7. painos. McGraw Hill
5. Sevillan yliopisto. Kitkavoimat. Toipunut: Laplace.meille.On.