Keskipakovoiman kaavat, kuinka lasketut, esimerkit, harjoitukset

Se keskipakoisvoima on taipumus työntää vartaloa, jotka kääntyvät käyrän ottamiseen. Sitä pidetään yhtenä kuvitteellinen voima, pseudofuerza jompikumpi hitausvoima, koska se ei johdu todellisten esineiden välisistä vuorovaikutuksista, vaan se on osoitus inertia ruumiista. Hitaus on ominaisuus, joka saa esineet haluamaan pitää lepo- tai yhtenäisen suorakulmaisen liikkeen, jos heillä on se.

Termin "keskipakoisvoima" on keksinyt tiedemies Christian Huygens (1629-1695). Hän vakuutti, että planeettojen kaarevaa liikettä taipumus siirtää ne pois, ellei aurinko käyttänyt jonkin verran voimaa säilyttääkseen ne ja laski, että tämä voima oli verrannollinen nopeuden neliöön ja käänteisesti verrannollinen kuvatun kehän säteen kanssa.

Kuvio 1. Käyrän antamisessa matkustajat kokevat voiman, jolla on taipumus päästä ne pois siitä. Lähde: Libreshot.

Niille, jotka matkustavat autolla, keskipakovoima ei ole ollenkaan kuvitteellinen. Oikealle tunteelle kääntyvän auton matkustajat ajavat vasemmalle, ja päinvastoin, kun auto kääntyy vasemmalle, ihmiset kokevat voiman oikealle, joka näyttää haluavan siirtää heidät pois käyrän keskustasta.

Keskipakovoiman suuruus F_g Se lasketaan seuraavalla lausekkeella:

 Missä:

-F_g Se on keskipakovoiman suuruus

-m Se on esineen massa

-v Se on nopeus

-R - Se on kaareva radan säde.

Voima on vektori, joten rohkeaa kirjainta käytetään erottamaan se sen suuruudesta, mikä on skalaari.

Sinun on aina pidettävä mielessä, että F_g ilmestyy vain, kun liike kuvataan nopeutetulla referenssijärjestelmällä.

Alussa kuvattussa esimerkissä kiertävä kiertue muodostaa kiihtyneen viitteen, koska se vaatii centripetaalinen kiihtyvyys, jotta voin kääntyä.

[TOC]

Kuinka keskipakoisvoima lasketaan?

Vertailujärjestelmän valinta on elintärkeä liikkeen arvioimiseksi. Kiihdytetty vertailujärjestelmä tunnetaan myös nimellä ei -on -inertiaalinen järjestelmä.

Tämän tyyppisessä järjestelmässä, kuten pyörivä auto, ilmestyy kuvitteelliset voimat, kuten keskipakoisvoima, joiden alkuperä ei ole todellinen vuorovaikutus esineiden välillä. Matkustaja ei voinut sanoa, mikä työntää hänet pois käyrästä, hän voi vain vahvistaa, mitä näin tapahtuu.

Toisaalta inertiaalisessa referenssijärjestelmässä vuorovaikutukset annetaan todellisten esineiden, kuten liikkeen ja maan, välillä, mikä johtaa painoon tai kehon ja sen välillä, jolla se liikkuu, joka lähtee kitkaa ja kitkaa ja normaali.

Tien reunalla seisova tarkkailija ja joka näkee auton antavan käyrän, on hyvä esimerkki inertiaalisesta vertailujärjestelmästä. Tätä tarkkailijaa varten auto pyörii, koska se käyttää voimaa, joka on suunnattu kohti käyrän keskustaa, joka pakottaa hänet olemaan poistumatta siitä. Kyse on Centripetal Force, joka on tuottanut kitka renkaiden ja jalkakäytävän välillä.

Inertiaalisessa referenssijärjestelmässä keskipakovoimaa ei näytetä. Siksi ensimmäinen vaihe laskemaan se on valita huolellisesti viitejärjestelmä, jota käytetään kuvaamaan liikettä.

Se voi palvella sinua: herkkä lämpö: Konsepti, kaavat ja harjoitukset ratkaistu

Lopuksi on huomattava, että inertiaalisten referenssijärjestelmien ei pitäisi välttämättä olla levossa, kuten tarkkailija, joka tarkastelee ajoneuvoa käyrän antamiseksi. Inertiaalinen referenssijärjestelmä, joka tunnetaan nimellä Laboratorioviitekehys, Se voi myös olla liikkeessä. Tietenkin, jatkuvan nopeuden kanssa inertiaalista.

Vapaa kehon kaavio inertiaalisessa ja ei-interl-järjestelmässä

Seuraavassa vasemmalla olevassa kuvassa tarkkailija tai seisoo ja katselee O ', joka on laiturilla, joka pyörii ilmoitettuun suuntaan. O: lle, joka on inertiaalinen kehys, varmasti tai 'ylläpidetään kääntämällä centripetaalin voiman vuoksi F_c Tuottama ruudukkoseinä O ': n takana.

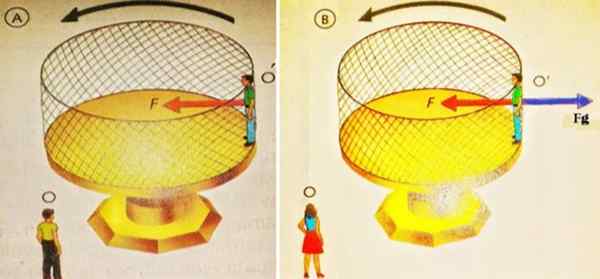Kuva 2. Pyörivällä alustalla seisova. Lähde: Santillana -fysiikka.

Vain inertiaalisissa referenssijärjestelmissä on pätevä soveltaa Newtonin toista lakia, jossa todetaan, että nettovoima on yhtä suuri kuin massan tuote kiihtyvyydellä. Ja niin, että se on esitetty vapaan kehon kaavio, se saadaan:

F_c = MA_c

F_c= MV² / R

Samoin oikeassa kuvassa on myös vapaa kehon kaavio, joka kuvaa sitä, mitä tarkkailija näkee tai '. Hänen näkökulmastaan ​​hän on levossa, joten hänen voimansa ovat tasapainossa.

Nämä voimat ovat: normaalit F, että seinä käyttää sitä, punaisella ja suunnattu kohti keskustaa ja keskipakoisvoimaa F_g Se työntää sen ulos ja joka ei ole peräisin vuorovaikutuksesta, se on ei-auto.

Keskipakovoima, joka on kuvitteellinen, tasapainottaa todellinen voima, kosketus tai normaali voima, joka osoittaa keskustaan. Siksi:

∑f_x = 0 → F_g - F = 0

F_g = F

Esimerkit

Vaikka keskipakoisvoimaa pidetään pseudo -räikeänä, sen vaikutukset ovat melko todellisia, kuten seuraavissa esimerkeissä voidaan nähdä:

- Missä tahansa huvipuiston kiertävässä pelissä keskipakovoima on läsnä. Hän huolehtii siitä, että "pakenemme keskustasta" ja tarjoaa jatkuvaa vastarintaa, jos yrität kävellä kohti liikkuvan karuselin keskustaa. Seuraavassa heilurissa voit nähdä keskipakovoiman:

Voi palvella sinua: Eugen Goldstein: Elämäkerta, panokset ja löytöt

https: // giphy.com/gifs/jtu3pnmkqomqdujwmo

- Coriolis -vaikutus syntyy maanpäällisestä rotaatiosta, joka saa maan lakkaa olemasta inertiaalista kehystä. Sitten Coriolisin voima näyttää, että pseudo-voima, joka sivusuunnassa ohjaa esineet, kuten ihmisten kanssa, jotka yrittävät kävellä pyörivällä alustalla.

https: // giphy.com/gifs/the-x-files-sully-mulder-funlglkhobs

Harjoitukset

Harjoitus 1

Auto, joka pyörii kiihtyvyydellä -Lla Oikealla puolella hän kantaa täytetyn lelun, joka roikkuu sisäisestä taustapeilistä. Piirrä ja vertaa leluvapaat runkokaaviot osoitteesta:

a) tien päällä seisovan tarkkailijan inertiaalinen referenssikehys.

b) Autossa kulkeva matkustaja.

Liittää jhk

Tiellä seisova tarkkailija varoittaa, että lelu liikkuu nopeasti kiihtyvyydellä -Lla oikealle.

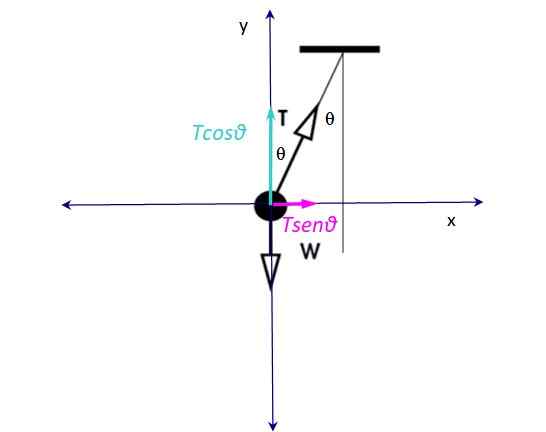Kuva 3. Ilmainen kehon kaavio harjoitukselle 1A. Lähde: f. Zapata.

Leluilla on kaksi voimaa: toisaalta köyden jännitys T ja pystysuora paino alaspäin W -. Paino on tasapainossa jännityksen pystysuuntaisen komponentin kanssa Tcosθ, siksi:

W - tcosθ = 0

Jännityksen vaakasuora komponentti: T. Sentr Se on epätasapainoinen voima, joka on vastuussa kiihtyvyydestä oikealle, joten centripetaalinen voima on:

F_c= T.senθ = ma_c

Ratkaisu b

Auton matkustajalle lelu roikkuu tasapainossa ja kaavio on seuraava:

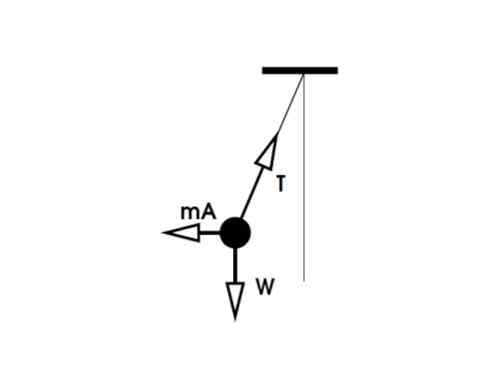Kuva 4. Ilmainen kehon kaavio harjoitukselle 1B. Lähde: f. Zapata.

Kuten edellisessä tapauksessa, jännityksen paino ja pystysuuntainen komponentti kompensoidaan. Mutta vaakasuuntainen komponentti on tasapainossa kuvitteellisella voimalla F_g = MA, jotta:

-Ma + tsenθ = 0

F_g = MA

Harjoitus 2

Valuutta on vanhojen vinyylitehtävien reunalla, jonka säde on 15 cm ja pyörii nopeudella 33 kierrosta / minuutti. Löydä valuutan ylläpidon välttämätön staattinen kitkakerroin valuutan valuuttaan käyttämällä valuuttaa.

Ratkaisu

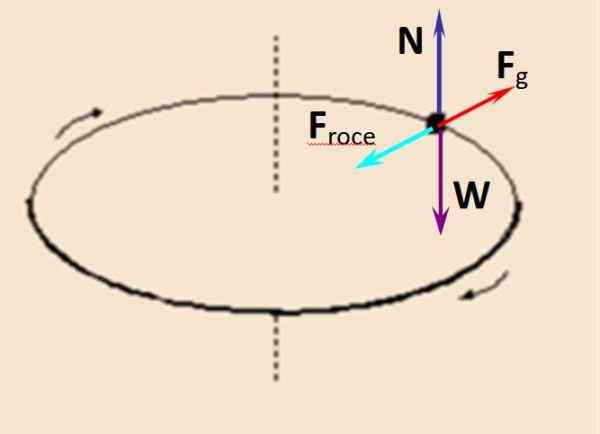
Kuvassa on vapaa kehon kaavio tarkkailijalle, joka liikkuu valuuttaan. Normaali N että Toadiscos kulkee pystysuunnassa ylöspäin tasapainottaa painoa W -, kun taas keskipakovoima F_g kompensoi staattinen hankaus F_kosketus.

Kuva 5. Ilmainen kehon kaavio harjoitukselle 2. Lähde: f. Zapata.

N - w = 0

F_kosketus - F_g = 0

Keskipakovoiman suuruus on MV²/R, Kuten alussa todettiin, sitten:

F_kosketus = F_g = MV²/R

Toisaalta staattinen kitkavoima on antanut:

Voi palvella sinua: Volt tai Volt: Konsepti ja kaavat, vastaavuudet, esimerkit

F_{RECO =} μ_s.N

Missä μ_s Se on staattinen hankauskerroin, vapautettu määrä, jonka arvo riippuu siitä, kuinka pinnat ovat kosketuksessa. Tämän yhtälön korvaaminen on edelleen:

μ_s.N = mv²/R → μ_s = MV²/R.N

Olisi tarpeen määrittää normaalin suuruus, joka liittyy painoon n = mg mukaan. Korvaa uudelleen:

μ_s = MV²/R.mg → μ_s = v²/Rg

Takaisin lausuntoon, tämä raportoi, että valuutta pyörii nopeudella 33 kierrosta minuutissa, mikä on kulmanopeus tai kulmataajuus Ω, liittyy lineaariseen nopeuteen v-

v = ω.R = 33 kierrosta/min . 2π Radianit/Rev . 15 cm . (1 min/60 s) = 51. 8 cm/s

μ_s = v²/RG = (51.8 cm/s)²/ (15 cm x 981 cm/ s²) = 0.18

Tämän harjoituksen tulokset olisivat olleet samat kuin valinneet inertiaalisen referenssijärjestelmän. Tässä tapauksessa ainoa voima, joka kykenee aloittamaan kiihtyvyyden keskustaa kohti, on staattinen kosketus.

Sovellukset

Kuten olemme sanoneet, keskipakovoima on kuvitteellinen voima, jota ei näy inertiauskehyissä, jotka ovat ainoat, joissa Newtonin lait ovat päteviä. Niissä Centripetal Force on vastuussa kehon tarjoamisesta tarvittava kiihtyvyys keskustaa kohti.

Centripetal -voima ei ole erilainen voima jo tiedossa. Päinvastoin, juuri ne tekevät centripetaalivoimien roolin tarvittaessa. Esimerkiksi painovoima, joka tekee kuun kiertoradan.

Koska kiihtyneitä referenssijärjestelmiä on kuitenkin runsaasti, kuvitteellisilla voimilla on hyvin todellisia vaikutuksia. Näytteelle tässä on kolme tärkeää sovellusta, joissa niillä on konkreettisia vaikutuksia:

Sentrifugaattorit

Sentrifugaattoreita käytetään laajasti välineitä laboratoriossa. Ajatuksena on saada seos aineita kääntymään suurella nopeudella ja aineet, joilla on suurempi massa, kokea suurempi keskipakovoima, alussa kuvatun yhtälön mukaan.

Sitten massiivisimmat hiukkaset pyrkivät siirtymään pois kierto -akselista, joten se on erotettu kevyimmistä, joka pysyy lähempänä keskustaa.

Pesukoneet

Automaattisissa pesukoneissa on erilaisia ​​puristusjaksoja. Niissä vaatteet sentrifugoivat jäljellä olevan veden poistamiseksi. Lisää syklin kierroksia, vähemmän märkä on vaatteet pesun lopussa.

Curve Peralte

Autot vievät käyrät teillä paremmin, tietä, joka nojautuu hiukan käyrän keskustaa, niin kutsutut peralte. Tällä tavalla auto ei riipu yksinomaan renkaiden ja tien välisestä staattisesta kitkasta käännöksen loppuun saattamiseksi poistumatta käyrästä.

Viitteet

1. Acosta, Victor. Didaktisen oppaan rakentaminen keskipakoisvoimiin sykliopiskelijoille v luokka 10.Palautettu: bdigital.I-kirjain.Edu.yhteistyö.
2. Toppr. Liikelaki: Liikeympyrä. Toipunut: Toppr.com.
3. Resnick, r. (1999). Fyysinen. Osa. 1. 3. ed. espanjaksi. Mannertoimitusyhtiö S.-Lla. C: n.V.
4. Hidalgon valtion autonominen yliopisto. Keskipakoisvoima. Palautettu: UAEH.Edu.MX
5. Wikipedia. Sentrifugaattorit. Palautettu: on.Wikipedia.org.