Jatkuva ominaisuusfunktio, esimerkit, harjoitukset

Se jatkuva toiminta Se on yksi, jossa arvo ja. Toisin sanoen: vakiotoiminnolla on aina muoto  f (x) = k, missä k -k - Se on todellinen numero.

Kuvaamalla vakiotoiminto koordinaattijärjestelmässä Xy, Se on aina suora viiva, joka on yhdensuuntainen vaakasuoran akselin tai akselin kanssa x.

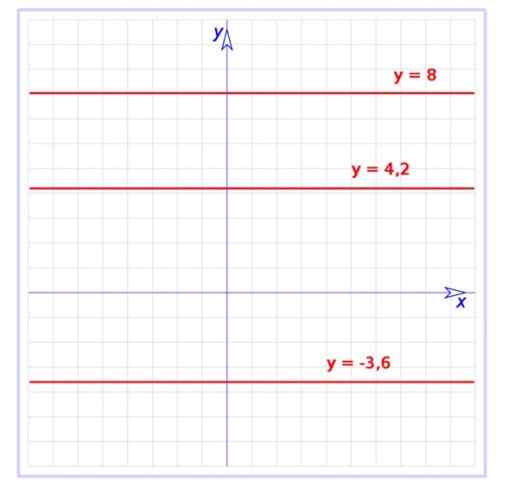
Kuvio 1. Kaavio useista vakiotoiminnoista Cartesian tasolla. Lähde: Wikimedia Commons. Käyttäjä: Hite [julkinen verkkotunnus]

Tämä toiminto on erityinen tapaus toiminto, jonka kuvaaja on myös suora viiva, mutta kaltevuudella. Vakiofunktiossa on vireillä oleva, toisin sanoen se on vaakasuora viiva, kuten kuvasta 1 nähdään.

Kolme vakiotoimintoa on kaavio:

f (x) = -3.6

G (x) = 4.2

H (x) = 8

Kaikki ovat suoraan vaakasuuntaisen akselin suuntaisesti, ensimmäinen on kyseisen akselin alapuolella, kun taas jäljellä olevat ovat yläpuolella.

[TOC]

Vakiofunktion ominaisuudet

Voimme tiivistää vakiofunktion pääominaisuudet seuraavasti:

-Sen kuvaaja on vaakasuora suora viiva.

-Sillä on ainutlaatuinen risteys akselin kanssa ja, arvoinen k -k -.

-Se on jatkuvaa.

-Vakiofunktion hallitseminen (arvojoukko x) on reaalilukujen joukko R -.

-Reitti, alue tai ristiriita (muuttuja ottaa arvojoukot ja) on yksinkertaisesti vakio k -k -.

Esimerkit

Toiminnot ovat välttämättömiä linkkien luomiseksi suuruuksien välillä, jotka riippuvat toisistaan ​​jollain tavalla. Nykyinen suhde niiden välillä voidaan mallintaa matemaattisesti tietääksesi kuinka toinen niistä käyttäytyy, kun toinen vaihtelee.

Voi palvella sinua: papruda

Tämä auttaa rakentamaan malleja monille tilanteille ja tekemään ennusteita heidän käyttäytymistään ja evoluutiostaan.

Ilmeisestä yksinkertaisuudestaan ​​huolimatta jatkuvalla toiminnolla on monia sovelluksia. Esimerkiksi, kun kyse on suurten suuruuksien tutkimisesta, jotka pysyvät vakiona ajassa tai ainakin huomattavana ajankohtana.

Tällä tavoin suuruudet käyttäytyvät sellaisissa tilanteissa, kuten seuraavat:

-Se nopeus Risteily autosta, joka liikkuu pitkällä suoraviivaisella moottoritiellä. Niin kauan kuin se ei lopeta tai kiihdytä, autolla on tasainen suorakulmainen liike.

Kuva 2. Jos auto ei lopeta tai kiihdytä, sillä on tasainen suorakulmainen liike. Lähde: Pixabay.

-Täysin ladattu ja irrotettu lauhdutin piiristä on a taakka jatkuva.

-Lopuksi tasainen pysäköinti ylläpitää a hinta jatkuvaa riippumatta siitä, kuinka kauan siellä pysäköity auto.

Toinen tapa edustaa jatkuvaa toimintoa

Jatkuva funktio vuorotellen voidaan esittää seuraavasti:

f (x) = kx^{0 -}

Koska kaikki arvot x Nostettu arvoon 0 antaa yhden seurauksena, edellinen lauseke pelkistetään tuttuun:

f (x) = k

Tietysti niin tapahtuu niin kauan kuin arvo k -k - on erilainen kuin 0.

Siksi vakiotoiminto luokitellaan myös a polynomifunktio luokka 0, muuttujan eksponentin jälkeen x Se on 0.

Ratkaisut

- Harjoitus 1

Vastaa seuraaviin kysymyksiin:

a) Voidaanko vahvistaa, että x = 4: n antama viiva on vakiofunktio? Syy vastauksesi.

b) Voiko vakiofunktiolla olla risteys x -akselin kanssa?

c) on funktio f (x) = w vakiona²?

Vastaa

Tässä on viivan x = 4 kaavio:

Voi palvella sinua: Tilastolliset muuttujat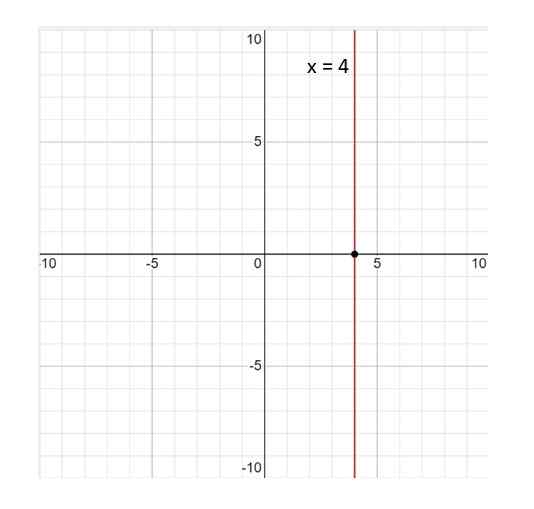 Kuva 3. Viivan X = 4 kaavio. Lähde: f. Zapata.

Rivi x = 4 ei ole funktio; Määritelmän mukaan funktio on suhde siten, että muuttujan jokainen arvo x Se vastaa yhtä arvoa ja. Ja tässä tapauksessa tätä ei täytetä, koska arvo x = 4 liittyy äärettömiin arvoihin ja. Siksi vastaus ei ole.

Vastaus b

Yleensä vakiofunktiolla ei ole risteystä akselin kanssa x, ellei se ole y = 0, jolloin se on akseli x Oikein sanottu.

Vastaus C

Kyllä, siitä lähtien W - Se on vakio, sen neliö on myös. Mitä kiinnostusta se on W - Se ei riipu tulomuuttujasta x.

- Harjoitus 2

Etsi risteys toimintojen välillä f (x) = 5 ja G (x) = 5x - 2

Ratkaisu

Näiden kahden toiminnon välinen risteys voidaan kirjoittaa vastaavasti uudelleen:

y = 5; y = 5x - 2

Ne ovat sovitettuja, hankkimalla:

5x - 2 = 5

Joka on ensimmäisen asteen lineaarinen yhtälö, jonka ratkaisu on:

5x = 5+2 = 7

x = 7/5

Risteyspiste on (7/5; 5).

- Harjoitus 3

Osoita, että vakiotoiminnosta johdettu on 0.

Ratkaisu

Johdannaisen määritelmästä:

 f (x) = k

f (x+h) = k

Määritelmän korvaaminen:

Edellä on järkevä. Vakiotoiminnolla on nolla vireillä ja myös sille tangenttiviiva.

Lisäksi, jos ajattelemme johdannaista valuuttakurssina Dy/dx, Jatkuva funktio ei kokee muutosta, joten sen johdannainen on mitätön.

Voi palvella sinua: Moninkertainen periaate: Laskentatekniikat ja esimerkit

- Harjoitus 4

Löytää määrittelemätön integraali f (x) = k.

Ratkaisu

- Harjoitus 5

Matkapuhelinyhtiö tarjoaa rajoittamatonta Internet -palvelua, jonka kiinteä hinta maksaa 15 dollaria kuukaudessa. Mikä on hintatoiminto ajan mukaan?

Ratkaisu

Olkoon p maksettava hinta ja t, joka voidaan ilmaista päivinä. Toiminto on vahvistettu seuraavasti:

P (t) = 15

- Harjoitus 6

Seuraava vs. aikakaavio vastaa hiukkasen liikettä.

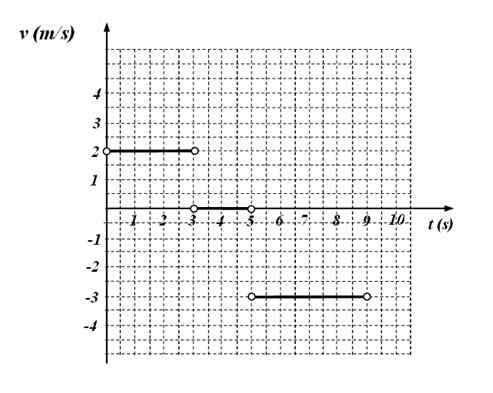Kuva 4. Toiminto V (t) -toimintokaavio harjoitukselle 6. Lähde: f. Zapata.

Sitä pyydetään:

a) Kirjoita lauseke nopeusfunktiolle ajan funktiona V (t).

b) Löydä matkapuhelimen kulkemat etäisyydet aikavälillä välillä 0 - 9 sekuntia.

Liittää jhk

Kaaviosta, joka osoittaa:

-V = 2 m/s Aikavälillä välillä 0–3 sekuntia

-Mobiili pidätetään 3–5 sekunnissa, koska tällä aikavälillä nopeus on 0 arvoinen.

-V = - 3 m/s 5–9 sekuntia.

Se on esimerkki kappaleista tai osien toiminnasta, joka puolestaan ​​koostuu vakiotoiminnoista, voimassa vain ilmoitetuille aikaväleille. Päätelee, että haluttu toiminto on:

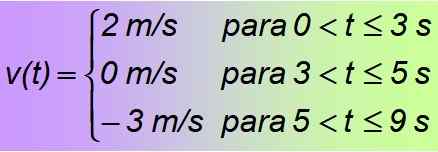
Ratkaisu b

Kaaviosta v (t) voidaan laskea matkapuhelimen kuljettama etäisyys, joka on numeerisesti yhtä suuri kuin alueen matala/käyrä. Tällä tavalla:

-Etäisyys kuljettu välillä 0–3 sekuntia = 2 m/s . 3 s = 6 m

-3–5 sekuntia hänet pidätettiin, siksi hän ei kulkenut etäisyyttä.

-5–9 sekunnin välinen etäisyys = 3 m/s . 4 s = 12 m

Kaiken kaikkiaan matkapuhelin kiertää 18 metriä. Katso, että vaikka nopeus on negatiivinen 5–9 sekunnin välein, kulkenut etäisyys on positiivinen. Mitä tapahtuu, että kyseisen ajanjakson aikana matkapuhelin oli muuttanut nopeuden merkitystä.

Viitteet

1. Geogebra. Vakiotoiminnot. Toipunut: Geogebra.org.
2. Maplesoft. Jatkuva funktio. Palautettu: Maplesoft.com.
3. Wikilibros. Laskenta muuttujaan/toimintoihin/vakiofunktioon. Palautettu: on.Wikibooks.org.
4. Wikipedia. Jatkuva toiminta. Haettu: vuonna.Wikipedia.org
5. Wikipedia. Jatkuva toiminta. Palautettu: on.Wikipedia.org.