Aste -toiminnot, jotka ovat suurempia kuin kaksi (esimerkit)

Arilla (polynomi), joka on suurempi kuin kaksi, on yleinen muoto:

f (x) = a_{0 -} + -lla₁x +a₂x² +.. .-lla_nxⁿ

N = 3, 4, 5,…, ei -negatiivinen kokonaisluku ja kertoimet_jompikumpi, -lla₁…_n, jotka ovat yleensä todellisia lukuja.

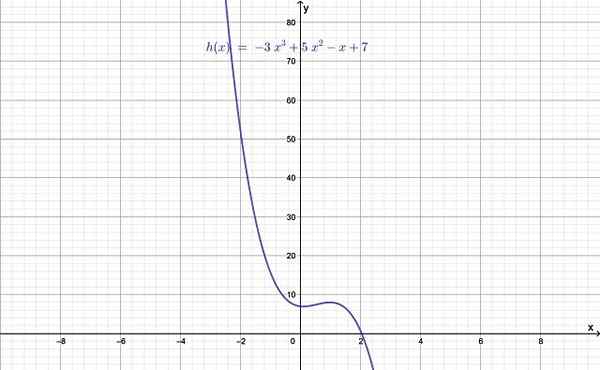Kuvio 1.- Aste -funktion kaavio yli 2. Lähde: f. Zapata.

Funktion aste annetaan n: n arvolla, suurin eksponenteista ja joka puolestaan ​​on suurempi kuin 2. Kun n = 0 on vakiofunktio, jos n = 1, se on lineaarinen funktio ja lopulta n = 2: lla, se on neliömäinen funktio.

Esimerkkejä yli kahden toiminnoista, muuttujassa "x", ovat seuraavat:

• f (x) = x³
• H (x) = - 3x³ + 5x² - X + 7
• g (x) = x⁴ - 6x² + 25

Funktio f (x) = x³ Se on yksinkertaisin kaikista yli kahden toiminnoista ja sen aste on 3. Tutkinto 3 tunnetaan myös nimellä kuutiometri. G (x) on luokka 4, koska se on 4: n enimmäiskonponentti.

N: n arvo on erittäin tärkeä, koska se määrittää kaavion yleisen muodon ja myös suurimman määrän juuria tai risteyksiä, jotka toiminnolla on vaakasuoran akselin kanssa. Itse asiassa 3 -luokan funktio koskettaa vaaka -akselia korkeintaan 3 pisteessä, yksi luokasta 4 tekee sen korkeintaan 4 pisteessä ja niin edelleen.

Mitä tahansa riippumattomaan termiin, minkä tahansa asteen polynomifunktiossa se osoittaa toiminnan leikkauksen pystysuoran akselin kanssa.

Yli kahden polynomifunktioiden ominaisuudet

Verkkotunnus

Funktion alue on arvojoukko, joka mahdollistaa y = f (x): n arvojen laskemisen. Polynomifunktioissa tämä joukko on todelliset N -numerot tai kompleksilukujoukko, tarvittaessa verkkotunnuksen pidentämiseksi.

Voi palvella sinua: Trigonometriset rajat: Kuinka ratkaista ne, ratkaistut harjoitukset

Tarkoittaa, että ottaen huomioon polynomifunktio f (x) = a_{0 -} + -lla₁x +a₂x² +.. .-lla_nxⁿ, Voit aina korvata minkä tahansa reaalilukun, suorittaa ilmoitetut toiminnot ja saada seurauksena arvon arvon y = f (x) oikea.

Etäisyys

Se on sarja, joka on muodostettu kaikki hankitut F (x) -arvot, ts. Kuvat, jotka jokaisella X: n arvolla on funktion f (x) kautta. Polynomifunktioille, jotka ovat suurempia kuin 2, tämä joukko on reaalilukuja.

Funktion juuret

Ovat x: n arvot, joille on täytetty, että f (x) = 0. Kuten edellä on osoitettu, funktion aste osoittaa sen enimmäismäärän, joka sillä voi olla, vaikka kaikki eivät ole välttämättä todellisia.

Kun funktion kertoimet ovat todellisia lukuja, todelliset juuret vastaavat funktion leikkauspisteitä X -akselin kanssa.

Esimerkki 1

Funktion f (x) = 2x rationaaliset juuret³ - 9x² + 7x + 6 löytyy seuraavan lauseen kautta:

Jos f (x) = a_{0 -} + -lla₁x +a₂x² +.. .-lla_nxⁿ Se on b/c -muoto, joten B: n mahdolliset arvot ovat a: n tekijöitä_jompikumpi ja C: n mahdolliset arvot ovat a: n tekijöitä_n.

Esimerkin funktiossa jo yksinkertaistetut yhdistelmät ovat: ± 6, ± 3, ± 2, ± 1, ± 3/2, ± ½. Nyt jokainen testataan esimerkiksi synteettisen jakautumismenettelyn avulla. Kun divisioonan jäännös on 0, todistettu arvo on juuri:

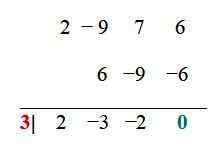
Arvo x₁ = 3 on funktion juuri tai nolla, siksi (x - 3) on yleinen tekijä f (x): lle, ja tämä voidaan kirjoittaa seuraavasti:

Se voi palvella: yhtenäinen ympyrä: trigonometriset toiminnot ja sovellukset

f (x) = (x - 3) ∙ (2x² −3x −2)

Jäljellä olevat kaksi juuria ovat arvot, jotka tyydyttävät 2x -yhtälön² −3x −2 = 0. Tämä yhtälö voidaan ratkaista yleisen kaavan, tieteellisen laskimen kautta tai toistaa edellisen Tanteo -prosessin.

Nämä juuret ovat x₂ = 2 ja x₃ = - ½, ja nyt f (x) voidaan kirjoittaa kolmen tekijän tuote:

f (x) = (x - 3) ∙ (x - 2) ⋅ (x + ½)

F (x): n risteykset X -akselin kanssa ovat pisteitä: P₁ (3.0), P₂(2.0) ja P₃(−½, 0). Geogebralla saatu funktion kaavio näyttää sen leikkaust X -akselin kanssa:

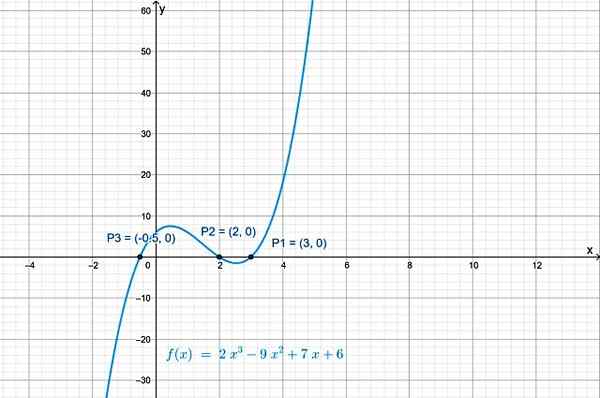Kuva 2.- Luokan 3 polynomifunktiolla on kolme risteystä vaakasuoran akselin kanssa. Lähde: f. Zapata.

Risteys pystysuoran akselin kanssa

Jos haluat löytää funktion leikkauspisteen pystysuoran akselin kanssa, sinun on löydettävä F (0), joka on yksinkertaisesti_{0 -}.

Esimerkki 2

Etsi F (x) = 2x leikkauspiste³ - 9x² + 7x + 6 pystysuoralla akselilla se on hyvin yksinkertainen, kun teet x = 0 f (x): ssä, se saadaan:

f (x) = 6

Ja funktion leikkauspiste pystysuoran akselin kanssa on P₄(0,6).

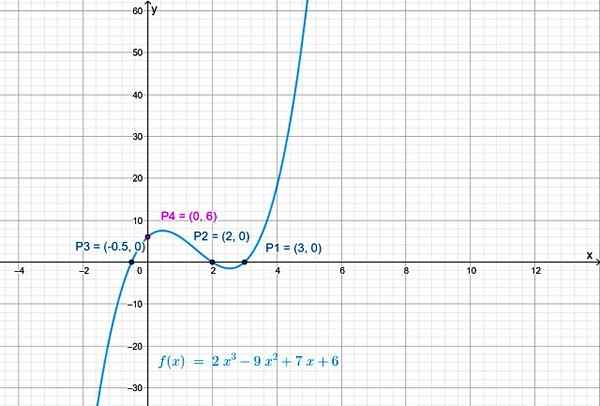Kuva 3. Käyrän leikkaus pystysuoran akselin kanssa on x = 0 f (x): ssa. Lähde: f. Zapata.

Jatkuvuus

Polynomiset funktiot yleensä ja erityisesti yli 2: n toiminnot ovat jatkuvia funktioita koko alueella, tämä tarkoittaa, että heillä ei ole hyppyjä, vaiheita, reikiä tai arvoja, joille niitä ei ole määritelty. Heillä ei myöskään ole asymptootteja, jotka ovat pystysuuntaisia, vaakasuoria tai vinoja, joihin funktio lähestyy ylittämättä niitä ylittämättä niitä.

Näitä pehmeyden ja jatkuvuuden ominaisuuksia arvostetaan yllä esitetyissä kaavioissa.

Kaavio yli 2: n toiminnoista

Kaaviot yli 2: n toiminnoista ovat jatkuvia ja pehmeitä, ja niiden muoto riippuu polynomin asteesta.

Voi palvella sinua: Permutaatiot ilman toistamista: kaavat, esittely, harjoitukset, esimerkit

Esimerkiksi luokan 3 REAM: llä sillä on negatiivinen merkki termillä, jolla on korkein aste).

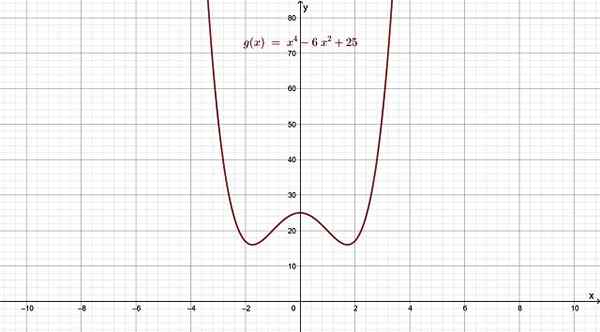Kuva 4. Luokan 4 polyinominen funktio, jonka kaavio muistuttaa kirjainta W. Lähde: f. Zapata.

X = 0: sta, sekä vasemmalla että oikealla arvolla, funktio käyttäytyy kuinka suurimman määrän termi tekisi, koska tämä vallitsee muiden yli, kun X: stä tulee erittäin suuri tai hyvin pieni.

Verrattuna kuvassa, joka seuraa funktiota f (x) = 2x³ - 9x² + 7x + 6 toiminnolla r (x) = x³ Ja on ymmärrettävä, että molempien käyrien muoto on samanlainen kuin X: n arvot, jotka ovat kaukana x = 0.

Suurten X -arvojen osalta funktio kasvaa nopeasti hoitamalla +∞, kun taas negatiivisten x -arvojen osalta funktio laskee nopeasti ja yleensä −∞.

Kuva 5.- Kaikki luokan N toiminnot käyttäytyvät samalla tavalla, kun ne siirtyvät pois x = 0: sta, sekä vasemmalle että oikealle. Lähde: f. Zapata.

Vertaamalla vääntömomentti -luokan käyriä (kuva 4) parittoman asteen kanssa (kuva 2), kunhan korkeimman luokan termillä mukana oleva kertoimella on sama merkki, havaitaan, että pariton asteen käyrät alkavat “Y” -negatiivisesta ja negatiivisesta kasvaa, kun taas kohderyhmä alkaa "y" positiivisesti ja vähenevät.

Viitteet

1. Barnett, r. 2000. Precculment: toiminnot ja grafiikat. Neljäs. Painos. McGraw Hill.
2. Laskeminen.DC. Polynomiset funktiot. Palautettu: laskelma.DC.
3. Larson, r. 2012. Ennakkoluulo. Kahdeksas. Painos. Cengage -oppiminen.
4. Stewart, J. 2007. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
5. Varsity -tutorit. Polynomifunktioiden piirtäminen. Haettu: WarsityTorm.com.