Matemaattiset toiminnot

Matemaattinen funktio on kahden suuruuden välinen suhde, kun ensimmäinen riippuu toisesta. Suljettu

Mitkä ovat matemaattiset toiminnot?

Se matemaattiset toiminnot Ne ovat kahden muuttujan välisen suhteen matemaattisen kielen ilmaus, ja ensimmäisen muuttujien arvo riippuu toisesta. Normaalisti nämä muuttujat symboloidaan kirjaimilla x ja y.  Muuttujaa X kutsutaan domeeniksi tai riippumattomaksi muuttujaksi; ja Y: lle, codominium tai riippuvainen muuttuja.

Katsotaanpa esimerkkiä. Meillä on kaksi muuttujaa tai suuruus: dollari ja senttiä. Tiedämme, että 100 senttiä vastaa dollaria. Siksi sentti (x) on alue ja dollari (y) vastaa codominiumia. Tämä suhde voidaan ilmaista seuraavalla toiminnolla (f):

F (x) = y / 100

Jos minulla on 143 senttiä säästöpankissani, ja haluan tietää kuinka monta dollaria olen tallentanut, käytän vain toimintoa:

F (x) = 143 /100

Siksi minulla on 1,43 dollaria.

Voimme myös ilmaista käänteisen suhteen, ts. Dollarin vastaa 100 senttiä. Näin ollen muuttujien luokat sijoitetaan: Dollarista (x) tulee verkkotunnus, kun taas senttiä on codominium. Ilmaisemme sen tällä tavalla:

F (x) = x x 100

Jos minulla on 1,43 dollaria piggy -pankissani, mutta haluan tietää kuinka monta senttiä tämä luku on vastaava, se riittää soveltamaan tätä toista toimintoa.

F (x): 1,43 x 100

Tulos palaa 143 alkuperäiseen senttiini.

Matemaattisten funktioiden muuttujat

Muuttuja on yksinkertaisesti symboli (x, y, z), joka edustaa erilaisia ​​elementtejä.

Edellisessä esimerkissä muuttujat x ja y symboloivat dollarin ja dollarin penniäkään. Mutta samoja symboleja (x ja y) voidaan käyttää edustamaan elementtien äärettömyyttä, kuten: henkilön ikä ja heidän painonsa; Lentojen lukumäärä tiettyyn määränpäähän ja ajanjaksoon (viikossa, kuukaudessa, vuodessa) jne.

Voi palvella sinua: synteettinen jako

Muuttujat voidaan luokitella lukuisiin tyyppeihin, mutta matemaattisten funktioiden merkityksellisimmät ovat seuraavat:

• Riippuva muuttuja: Ne, joiden arvo riippuu arvosta, joka on osoitettu muille funktion muuttujille.
• Itsenäinen muuttuja: Tämän tyyppisen muuttujan muutokset vaikuttavat funktion muiden muuttujien arvoihin.
• Kvantitatiivinen muuttuja: Se ilmaistaan ​​määriteltyjen numeeristen määrien avulla. Ne voivat olla kokonaisia ​​tai desimaalilukuja.

Matemaattisten toimintojen ominaisuudet

1- Muuttujien välinen suhde ilmaistaan ​​vastaavuutena.

2- Jokaiselle muuttujan x arvolle on a ja vain vastaava muuttuja ja. Ja päinvastoin: Y -tietyllä arvolla on A ja vain muuttujan x tulos.

3- Ne voidaan edustaa graafisesti Cartesian tasolla, mikä mahdollistaa yhden muuttujan käyttäytymisen ennustamisen toisesta.

4- Mathemaattisen toiminnan moderni määritelmä johtuu saksalaisesta matemaatikosta Peter Dirichlet (1805-1859), joka julkaisi sen vuonna 1837.

Matemaattisten toimintojen tyypit

Matemaattiset funktiot voidaan luokitella erilaisten kriteerien mukaan, kuten muuttujien X ja Y o: n välinen suhde funktion matemaattiseen käyttäytymiseen.

Päätyyppien joukossa ovat seuraavat:

Algebralliset toiminnot

Niille on ominaista luoda suhde komponenttien välillä, jotka ilmaistaan ​​joko monomiaalisen tai polynomin kautta. Tämä suhde voidaan määrittää yksinkertaisten matemaattisten operaatioiden, kuten vähennys, kertolasku, jako, summa, potentiaatio tai lähetys.

Lineaariset toiminnot

Kun ne esitetään kartesialaisella tasolla, ne ilmestyvät suoran linjan muodossa, joka leikkaa koordinaatti -akselin tietyssä vaiheessa. Siksi heidän nimensä, vaikka ne tunnetaan myös nimellä ensimmäisen asteen toiminnot.

Voi palvella sinua: Yleinen tekijä: Ominaisuudet, esimerkit, harjoitukset

Toiminnot palasiksi

Tämän tyyppisesti Codominium -arvo ja muuttaa funktion käyttäytymistä. Siksi on kaksi väliä, joilla on erilainen käyttäytyminen suhteessa verkkotunnuksen arvoon.

Transsendenttitoiminnot

Ne ovat erittäin monimutkaisia ​​toimintoja. Yleiset algebralliset toiminnot eivät riitä (vähennys, kertolasku, jako, summa, potentiaatio tai säteily) muuttujien välisen suhteen määrittämiseksi, joten muita matemaattisia työkaluja on käytettävä, kuten johdannaiset, integraalit tai logaritmit.

Trigonometriset toiminnot

Tämäntyyppiset toiminnot osoittavat numeerisen suhteen, joka on olemassa kolmion eri elementtien ja muiden geometristen hahmojen välillä, etenkin sen kulmien keskuudessa. Rinnan, kosinin, tangentin, Secant ja Harmonte -kaavat ovat esimerkkejä tämän tyyppisistä toiminnoista.

Injektiiviset toiminnot

Tämän tyyppisille toiminnoille on ominaista domeenin ja codominiumin välisen suhteen erityisyys. Jokaiselle jälkimmäisen arvolle vain yksi verkkotunnuksen arvo vastaa. Voi myös tapahtua, että verkkotunnusarvolla ei ole vastaavaa arvoa Codominiumissa.

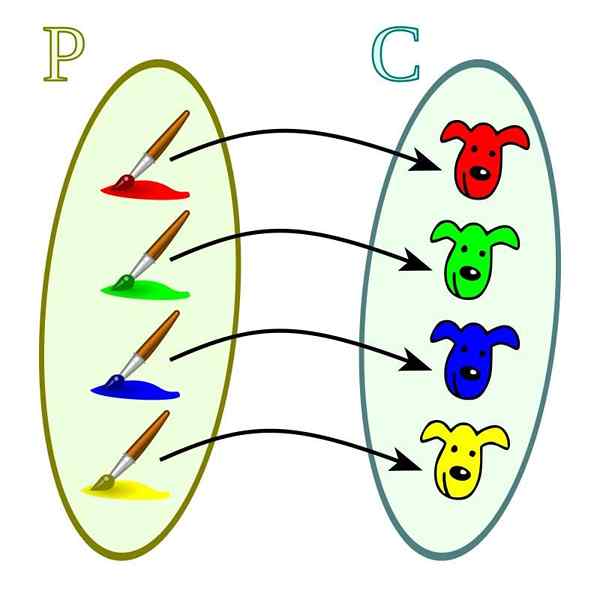Injektiotoiminto. Lähde: Wikimedia Commons

Onjektiivitoiminnot

Tässä tapauksessa jokainen kodominiumin suuruus liittyy ainakin yhteen verkkotunnuksen arvoihin. Ne erotetaan injektiofunktioista, joissa Codominium -arvot voivat liittyä useampaan kuin yhteen verkkotunnuksen arvoihin.

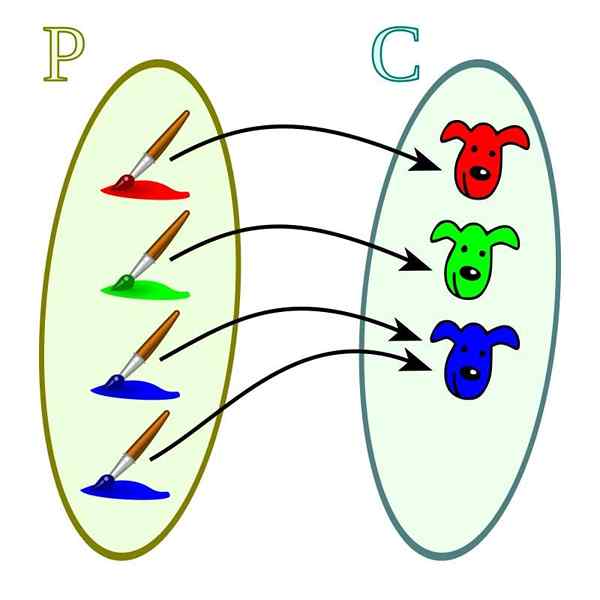Liiallinen toiminto. Lähde: Wikimedia Commons

Bijektiivifunktiot

Tämäntyyppiset toiminnot esittävät sekä injektiivisia että yliarviointeja.

Mitkä ovat matemaattisia toimintoja?

Toimintoja käytetään laajasti kaikissa tieteissä, joilla on matematiikka aputieteinä. Näin on fysiikka, tekniikka, lääketiede, rahoitus, tilastotiedot, muun muassa.

Voi palvella sinua: Taajuuden jakautuminen: Kuinka tehdä taulukko, esimerkki, liikunta

Jokapäiväisessä elämässä

Voimme kuitenkin olla hyödyllisiä myös yksinkertaisempien päivittäisten ongelmien ratkaisemisessa.

Kuvittele, että isoisäsi on antanut sinulle 10 kolikkoa, jotka vietät suklaalle. Kioskissa olet antanut 10 kolikkoa huollettavalle, käskemällä hänelle antamaan sinulle kaikki suklaat, joita voidaan ostaa kyseisellä valuutolla. He ovat antaneet sinulle 5 suklaata. Mikä on kunkin hinta?

Ehdotamme ongelmaa: Jos 5 suklaata vastaa 10 kolikkoa, niin kuinka monta kolikkoa se vastaa yhtä suklaata?

Riippumaton muuttujamme (x) on suklaan määrä (5), kun taas riippuvainen muuttuja (Y) vastaa valuuttojen lukumäärää, ts. 10.

Ilmaisemme funktion seuraavasti:

F (x) = 2x/x

F (x) = 2 (5)/5

F (x) = 10/5

F (x) = 2

Ja meillä on jo vastaus: jokainen suklaa maksaa 2 kolikkoa.

Viitteet

1. (S/F). Alkeisfunktiot. Matemaattiset funktiot sivusto. Otettu unetioista.Susi.com.
2. (S/F). Mikä on funktio? Otettu MathSisfunista.com.