Trigonometriset perustoiminnot, Cartesian tasossa, esimerkkejä, liikunta

Se trigonometriset toiminnot Oikea muuttuja, ne vastaavat mitä tahansa kulmaa (ilmaistuna radianeissa), trigonometrinen syy, joka voi olla sinia.

Tällä tavoin meillä on kuusi trigonometristä toimintoa: sinus, kosiini, tangentti, harvesteri, kuivaus ja kotagentti.

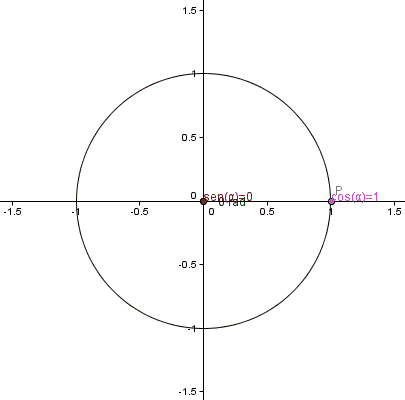Kuvio 1. Trigonometrinen ympyrän animaatio. Lähde: Wikimedia Commons.

Kulmien trigonometriset funktiot välillä 0 - 2π määritetään Radio 1: n yhtenäisen ympärysmittan avulla ja jonka keskus vastaa Cartesian -koordinaattijärjestelmän alkuperä: The Point (0.0).

Voimme löytää minkä tahansa koordinaattien (x, y) pisteen P P: n.

Segmentti, joka yhdistää alkuperän P: llä, yhdessä vastaavien segmenttien kanssa, jotka yhdistävät P: n projektiot koordinaattiakseleilla, muodostavat suorakulmion kolmion, jonka trigonometriset syyt tunnetaan nimellä osuus kolmion sivujen välillä. Niin:

• sin θ = vastapäätä /hypotenusa catoto
• cos θ = vierekkäinen /hypotenusa cateto
• tg θ = vastapäätä Cateto /viereinen cateto

Ja nyt syyt, jotka ovat yllä mainitun käänteinen:

• Sec θ = hypotenuse /vierekkäinen cateto
• Haittaa θ = hypotenusa /cateto vastapäätä
• ctg θ = vierekkäinen kateto /vastapäätä Catotoa

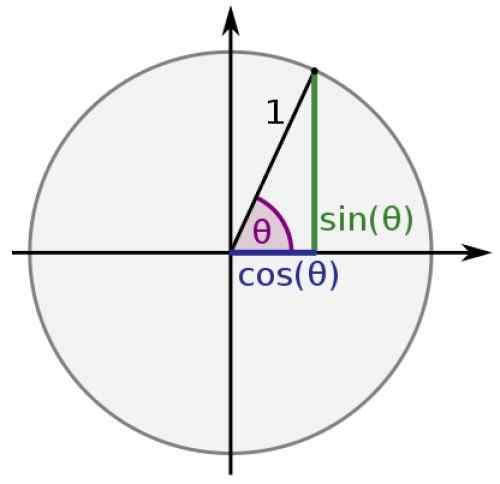
Yhtenäisessä ympyrässä minkä tahansa kolmion hypotenuse on yhtä suuri kuin 1 ja luokat ovat x: n ja y: n arvoisia, sitten:

sin θ = y

cos θ = x

Kuva 2. Oikea kolmio yksikköympyrässä. Lähde: Wikimedia Commons.

Tällä tavoin sini- ja kosinitoiminnot saavat aina arvot välillä -1 ja 1, kun taas jäljellä olevat:

tg θ = y/x

haittaa θ = 1/y

Sec θ = 1/x

Niitä ei ole määritelty milloin x jompikumpi ja Niiden arvo on 0.

[TOC]

Trigonometriset toiminnot Cartesian lentokoneessa

Kuten alla näemme, trigonometrisille funktioille on ominaista säännöllinen. Siksi ne eivät ole bijektiivia, paitsi rajoitetulla alueella.

Funktio f (x) = sin x

Alkaen trigonometrisestä ympyrästä pisteessä P (1.0), kulma on 0 radiaania. Sitten säde pyörii anti -horary -merkityksessä ja sen X -funktio kasvaa vähitellen, kunnes se saavuttaa π/2 radiaanit (90º), mikä vastaa 1.Noin 571 radiaania.

Voi palvella sinua: Lisäkulmat: Mitä ovat, laskenta, esimerkit, harjoitukset

Siellä se saavuttaa arvon y = 1 ja sitten se pienenee, kunnes se saavuttaa nollan π -radianeissa (180 °). Myöhemmin se pienenee vielä enemmän, koska arvo muuttuu negatiiviseksi, kunnes se saavuttaa −1, kun kulma on 3π/2 radiaania (270 °).

Lopuksi se kasvaa jälleen, kunnes se palaa nollaan 360 °: ssa, missä kaikki alkaa uudelleen. Tämä tekee y = sin x a määräajoin jakson 2π, joten sinusfunktio ei ole bijektiivi.

Lisäksi kuvaaja on symmetrinen pisteeseen (0,0), siksi funktio on pariton.

Sitten graafia y = sen x:

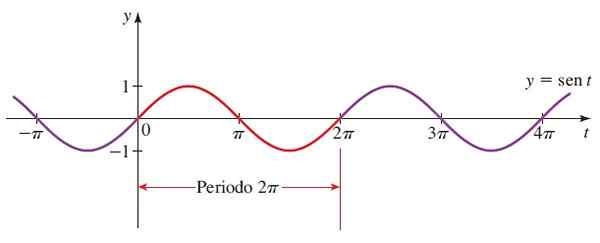Kuva 3. Toimintokaavio F (x) = sin x. Lähde: Stewart, J. Preculment: yliopiston matematiikka.

Punainen osa on ensimmäinen jakso. Myös negatiiviset kulmat otetaan huomioon, koska trigonometrisen ympyrän säde voi pyöriä aikataulussa.

Sen X -verkkotunnus = Kaikki oikeat.

Sen X -alue tai reitti = [-1,1]

Funktio f (x) = cos x

Kohdassa P (1.0) Coseno -funktio on 1 ja sieltä vähenee, saavuttaen 0, kun kulma on π/2. Jatka laskua ja ottaa negatiivisia arvoja, kunnes saavutat -1 kulmassa π.

Sitten se alkaa kasvaa vähitellen, kunnes se saavuttaa 0: n 3π/2: ssa ja saa arvon uudelleen, kun säde on kääntänyt täydellisen käännöksen. Sieltä sykli toistetaan, koska cos x on jaksollinen ja on myös vääntömomentti (symmetrinen pystysuoran akselin ympärillä).

Kosinifunktion muoto on sama kuin sinusfunktion, elleivät ne ole siirtyneet π/2: n suhteessa toiseen.

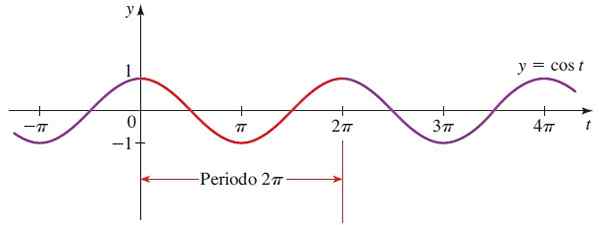Kuva 4. Toimintokaavio F (x) = sin x. Lähde: Stewart, J. Preculment: yliopiston matematiikka.

Cos x -alue = Kaikki oikeat.

Voi palvella sinua: Täsmällinen arvio

Etäisyys tai cos x -reitti = [-1,1]

Epäjatkuva trigonometriset toiminnot

Toiminnot TG X, CTG X, Sec X ja Hars. Koska nämä ovat arvoltaan 0 tietyissä kulmissa, kun ne ilmestyvät nimittäjään, he tekevät toiminnasta epäjatkuvasti.

Ja koska sinus ja kosiini ovat jaksollisia funktioita, toiminnot TG X, CTG X, Sec X, HAMM X ovat myös.

Tangenttifunktio f (x) = tg x

Tangenttifunktiossa epäjatkuvuusarvot ovat: ± π/2, ± 3π/2, ± 5π/2 ... Siellä funktio vie erittäin suuret tai hyvin pienet arvot. Yleensä tämä tapahtuu kaikille muodon (2n+1) π/2 -π -kerrannaisille, sekä positiivisille että negatiivisille, n = 0, 1, 2 ..

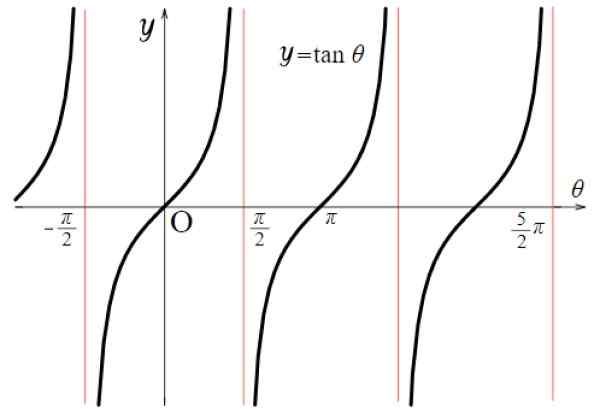Kuva 5. Toimintokaavio F (x) = TG x. Lähde: Wikimedia Commons.

Siksi:

TG X -verkkotunnus: D = x ∈ R - / x ≠ (2n+1) π/ 2; n ∈ Z -z

Rank tai TG X -kierros: Kaikki oikeat.

Huomaa, että funktio f (x) = tg x toistetaan välillä - π/2 ja + π/2, siksi sen ajanjakso on π. Lisäksi se on symmetrinen alkuperän suhteen.

Kotangenttifunktio f (x) = ctg x

Tätä toimintoa varten epäjatkuvuusarvot esiintyvät 0, ± π, ± 2π…, ts. Koko π -kertoimet.

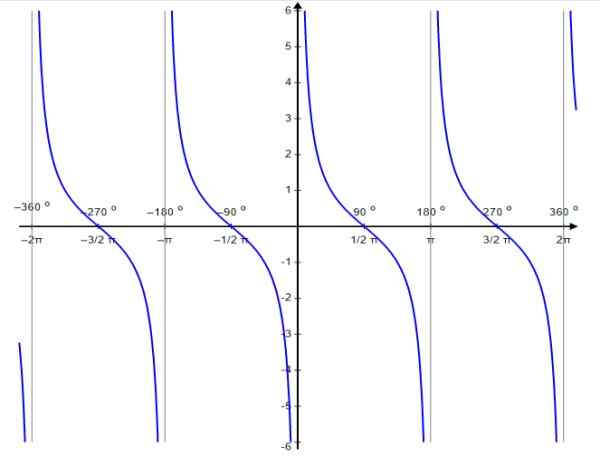Kuva 6. Toimintokaavio F (x) = coTg x. Lähde: Wikimedia Commons.

Kuten tangenttifunktio, kotangentti funktio on jaksollinen jakso π. Hänelle on toteutettu, että:

CTG X -alue: D = x ∈ R - / x ≠ n π; n ∈ Z -z

CTG X -alue tai reitti: Kaikki oikeat.

Kuivaustoiminto f (x) = sek x

SEC X -funktiolla on epäjatkuvuuspisteet ± π/2, ± 3π/2, ± 5π/2… missä cos x = 0. Se on myös jaksollinen jakso π ja sitä havaitaan myös kaaviosta, että funktio ei koskaan ota arvoja aikavälillä (-1,1)

Voi palvella sinua: kokonaiset numerot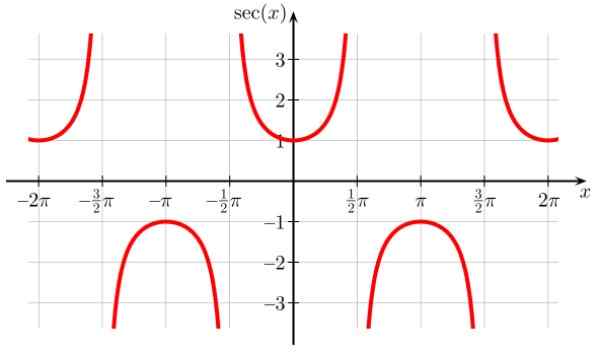 Kuva 7. Toimintokaavio F (x) = sek x. Lähde: Wikimedia Commons.

Sec x: n doma: D = x ∈ R - / x ≠ (2n+1) π/ 2; n ∈ Z -z

Sec x -alue tai reitti: Kaikki reaisit paitsi (-1,1)

Sadonkorjuufunktio f (x) = haittaa x

Se on samanlainen kuin kuivausfunktio, vaikka se on siirretty oikealle, siksi epäjatkuvuuspisteet ovat 0, ± π, ± 2π ja kaikki koko π -kertoimet. Se on myös määräajoin.

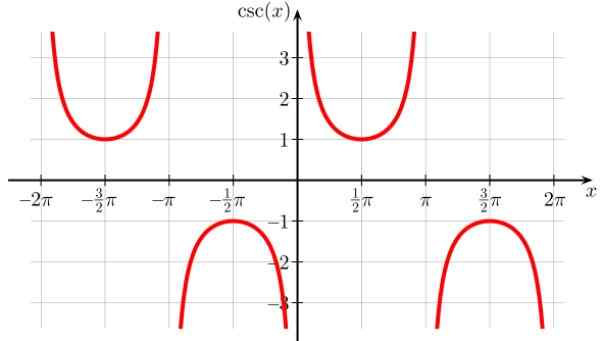Kuva 8. Toimintokaavio F (x) = haittaa x. Lähde: Wikimedia Commons. GEEK3/CC BY-SA (https: // creativecommons.Org/lisenssit/by-SA/4.0)

Vahingon alue X: D = x ∈ R - / x ≠ n π; n ∈ Z -z

Etäisyys tai harmoniareitti: Kaikki reaisit paitsi (-1,1)

Liikuntaa

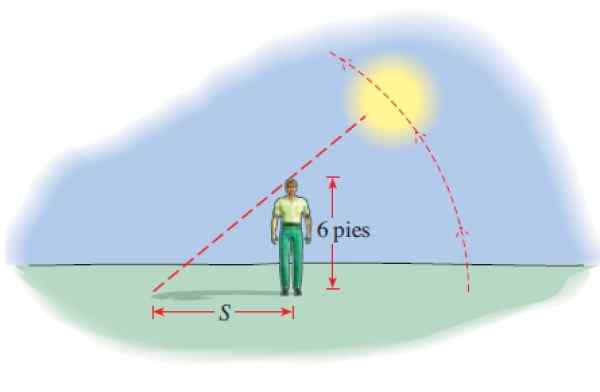
6 jalkaa pitkä mies projisoi sävyn, jonka pituuden on annettu:

S (t) = 6 │cot (π.T/12) │

S: llä jalkoissa ja T tuntien lukumäärä kello 6.00. Kuinka paljon varjo on klo 8, 12 m, klo 14.00 ja klo 17.45?

Ratkaisu

Meidän on arvioitava kunkin annetun arvon funktio, huomaa, että absoluuttisen arvon on oltava, koska varjon pituus on positiivinen:

-Klo 8 aamulla 2 tuntia on kulunut kello 6.00, siksi t = 2 ja s (t) on:

S (2) = 6 │cot (π.2/12) │Pies = 6 │Cot (π/6) │Pies = 10.39 jalkaa.

-Kun se on 12 n, t = 6 tuntia on kulunut, siksi:

S (6) = 6 │cot (π.6/12) │Pies = 6 │COT (π/2) │Pies = 0 jalkaa. (Tuolloin aurinko putoaa pystysuoraan henkilön päähän).

-Klo 14 he viettivät t = 8 tuntia:

S (8) = 6 │cot (π.8/12) │Pies = 6 │COT (2π /3) │Pies = 3.46 jalkaa.

-Kun on kello 17.45, 11 on ohittanut 11.75 tuntia klo 6.00, sitten:

S (11.75) = 6 │COT (π x 11.75/12) │pies = 91.54 jalkaa. Tällä hetkellä varjot ovat pidempiä.

Voiko lukija laskea ajan, jolloin henkilön varjo on yhtä suuri kuin heidän korkeutensa?

Viitteet

1. Carena, m. 2019. Preuniversity -matematiikan käsikirja. Rannikon kansallinen yliopisto.
2. Figuera, J. 1999. Matematiikka. Ensimmäinen. Monipuolinen. Bolivarian kollegiaaliset versiot.
3. Hoffman, J. Matematiikan aiheiden valinta. Osa 4.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.