Analyyttinen geometria

Selitämme, mikä analyyttinen geometria, sen historia, mitkä tutkimukset ja sovellukset ovat

Mikä on analyyttinen geometria?

Se analyyttinen geometria Se on matematiikan haara, jossa geometria ja algebra yhdistetään erilaisten geometristen ongelmien ratkaisemiseksi algebrallisten tekniikoiden avulla.

Käytä koordinaattijärjestelmiä, kuten Cartesian -koordinaattijärjestelmää, joka on nimeltään nimensä René Descartes. Tällä tavalla on mahdollista yhdistää käyrät tasossa ja avaruudessa, algebrallisilla yhtälöillä.

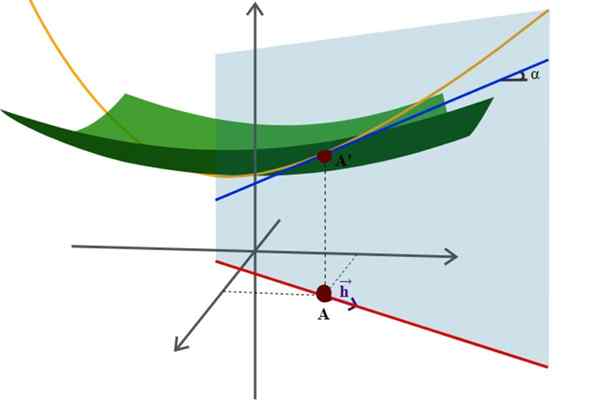Kaavio avaruuden pinnasta ja sen suuntajohdannaisesta, yksi monista analyyttisen geometrian edistyneemmistä sovelluksista. Lähde: Wikimedia Commons.

Esimerkki tästä on säteen r -riortion hyvin tunnettu yhtälö, joka keskittyy koordinaattijärjestelmän alkuperään:

Epäilemättä monissa tapauksissa on yksinkertaisempaa työskennellä käyrän algebrallisen ekspression kanssa kuin sen geometrisen esityksen kanssa. Tämä on tilanne laskettaessa käyrien välisiä risteyksiä tai niiden tangentti- tai kuivausviivojen löytämistä.

Samoin analyyttisen geometrian avulla on mahdollista asettua funktioita grafiikkaa. Ja kuten tiedetään, toiminnot mahdollistavat tieteen ja tekniikan ongelmien mallintamisen. Siksi analyyttinen geometria on läsnä näihin tietoalueisiin liittyvien uran opetussuunnitelmissa.

Lyhyt analyyttisen geometrian historia

Analyyttisellä geometrialla on alkuperän 1700-luvun ensimmäisellä puoliskolla kahden merkittävän ranskalaisen matemaatikon: René Descartes (1596-1650) ja Pierre de Fermat (1601-1665) käsin.

Rene Descartes

Voidaan kuitenkin sanoa, että hänen taustansa on vuosisatojen ajan pergamon kreikkalaisen matemaatikko Apollonius (262-190 a.C.-A. Hän kirjoitti tutkielman kartioista, joihin hän myönsi heidän nimensä: Ympyrä, ellipsi, vertaus ja hyperbola.

Se voi palvella sinua: Yhdistetty suhteellisuus: Selitys, kolme yhdistelmäsääntöä, harjoituksia

Siten Apollonion työ oli perusta, paljon myöhemmin Ranskan René Descartes ja Pierre de Fermat loivat analyyttisen geometrian perustan itsenäisesti. Mutta Descartesia pidetään tämän tieteen isänä, koska hän julkaisi ensimmäisenä teoksensa.

Descartes, Fermat ja Euler

Vuoden 1637 -menetelmän puheessa Descartes yhtenäisivät kaksi tieteenalaa, jotka siihen asti oli erotettu: algebra ja geometria. Descartes esittelee työssään Cartesian -koordinaattijärjestelmän, paikantaa pisteet lentokoneessa ja avaruudessa.

Se käyttää myös toisen asteen algebrallisia yhtälöitä kahdella muuttujalla, kuvaamaan kartiomaisia ​​osia ja on omistettu geometristen ongelmien ratkaisemiseksi niiden kanssa. Myös luoda hyvä osa tällä hetkellä käytettyä matemaattista merkintää.

Pierre de Fermat liittyy enemmän optiikkaan kuin analyyttiseen geometriaan, niiden vaikutukset ovat kuitenkin merkittäviä.

Vuonna 1629 Fermat jatkoi Pergamon Apolloniuksen kartioita ja loi analyyttisen geometrian muodostavat tekniikat, keksimällä oman koordinaattijärjestelmänsä ja määrittelemällä selvästi avainkonseptin Geometrinen paikka, jonka kanssa analyyttisen geometrian tutkimus alkaa.

Fermatin teokset kuitenkin näkivät valon vasta vuonna 1679, jonka hänen poikansa julkaisi, kun matemaatikko oli jo kuollut. Tästä syystä analyyttisen geometrian isyys johtuu Descartesista.

Myöhemmin ranskalaisten matemaatikkojen kanssa sveitsiläinen Leonardo Euler (1707-1783) perusti analyyttisen geometrian muodolliset emäkset. Euler esitteli useita koordinaattijärjestelmiä tasossa ja tilassa: suorakaiteen muotoiset, polaariset ja vinot koordinaatit sekä muutokset järjestelmästä toiseen.

Voi palvella sinua: Kuinka kyselyssä saadut tiedot?

Analyyttistä geometriaa koskevissa teoksissaan Euler syvensi myös eri käyrien luokitusta edustavan algebrallisen yhtälön (kolmas ja neljäs järjestys) asteen mukaan ja tutki sen ominaisuuksia intensiivisesti, tangenttien yhtälöt, kaarevat, symmetriat ja paljon lisää.

Mitä tutkimuksia analyyttinen geometria?

Yleisesti ottaen analyyttinen geometria keskittyy geometristen elementtien, kuten pisteiden, segmenttien, linjojen, käyrien, pintojen ja tilavuuksien tutkimiseen. Tätä varten, kuten edellä todettiin, se vahvistaa algebralliset yhtälöt, jotka kuvaavat ja yhdistävät nämä elementit, sallimalla niiden hallinnan algebrallisten tekniikoiden avulla.

Analyyttisen geometrian päätavoitteet ovat erittäin yhteenvetotavat seuraavat:

1. Luo Cartesian -koordinaattijärjestelmä ja polaarinen koordinaattijärjestelmä, jotta voidaan löytää pisteet tasossa, samoin kuin sen laajennus pisteisiin avaruudessa.
2. Piirrä segmentit, suorat, käyrät ja pinnat Cartesian tasoon ja tilaan.
3. Päätä yhtälöt, jotka kuvaavat analyyttisesti käyrää ja sen rakentamista tasolle ja/tai tilalle, samoin kuin kaikkien sen ominaisuuksien tutkiminen.
4. Luokitella käyrät, pinnat ja tilavuudet.
5. Johda perustavanlaatuiset kaavat ongelmien ratkaisemiseksi merkittävissä pisteissä, suorissa, suunnitelmissa, kulmissa, rinnakkaismissa, kohtisuorassa, etäisyyksissä, risteyksissä, alueet ja muut.
6. Ratkaise geometriset ongelmat soveltamalla algebrallisia menetelmiä, joille kaavat viittaavat merkittäviin pisteisiin, linjayhtälöihin, suunnitelmiin, kulmiin, pisteiden väliseen etäisyyteen, linjojen ja pisteiden välillä, tangenssipisteet, kuivat linjat, alueet, alueet ja paljon muuta.
7. Työskentele vektoritilojen ja tuotteiden kanssa vektorien välillä.

Kahden pisteen välinen etäisyys

Esimerkki analyyttisen geometrian lukuisista sovelluksista, yksi yksinkertaisimmista on tason kahden pisteen välisen etäisyyden laskeminen. Ovat kaksi pistettä p₁ Ja p₂, koordinaattien (x₁,ja₁) ja (x₂,ja₂) Vastaavasti etäisyys d niiden välillä lasketaan:

Voi palvella sinua: Trinomial

Polaarikoordinaatit

Tasopiste voidaan määrittää sen “R” -etäisyyden kautta koordinaattijärjestelmän alkuperään, nimeltään Polo, ja kulma, joka muodostaa viivan, joka sisältää pisteen ja navan, vaakasuoran akselin tai polaarisen akselin kanssa.

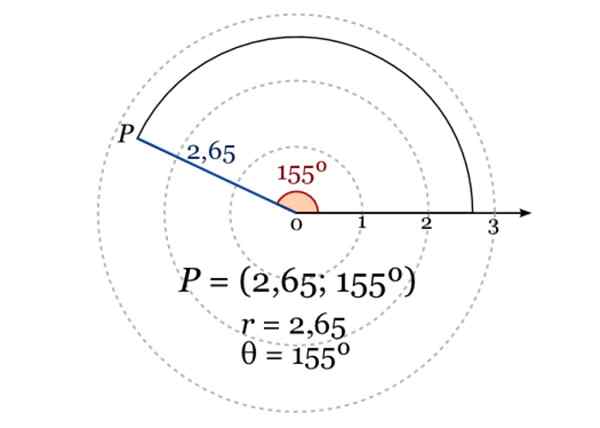Kuva näyttää pisteen P napakoordinaatit, joissa r = 2.65 ja kulma asteina polaariseen akseliin on 155º. Lähde: Wikimedia Commons.

Analyyttiset geometriasovellukset

Äärettömän pienen laskelman perusta

Analyyttinen geometria on välttämätöntä äärettömän pienen laskelman kehittämiselle, koska se helpottaa käyrien ja toimintojen graafista esitystä ja työskentelee niiden kanssa analyyttisellä tavalla, luodakseen malleja, jotka edustavat luonnon ilmiöitä.

Kartat

Cartesian koordinaattijärjestelmä auttaa tekemään karttoja ja tunnistamaan paikkoja leveysasteen ja pituuden kautta, mikä vastaa tasossa olevan pisteen Cartesian koordinaatit.

Topografiset laskelmat

Topografiassa käytetään erityyppisiä koordinaattijärjestelmiä, ja ne muodostavat sen tutkimuksen ja sovellusten perustan. Niiden joukossa on edellä kuvattu polaarinen koordinaattijärjestelmä.

Taivaankappaleet

Analyyttisen geometrian avulla kuvattuja kartiomaisia ​​osia osallistuvat tärkeisiin luonnon ilmiöihin, kuten taivaallisten kappaleiden etenemissuunnitelmiin, painopisteiden kohdalla. Esimerkiksi planeetat ja jotkut komeetit kuvaavat elliptisiä suuntauksia auringon ympärillä, tämä sijaitsee yhdessä valokeilassa.

Siviiliarkkitehtuuri ja rakenteet

Lukuisat käyrät ovat osa arkkitehtonisia rakenteita, esimerkiksi roikkuvan sillan kaapelit voivat olla vertauksia.

Globaalit paikannusjärjestelmät

Globaali paikannusjärjestelmä tai GPS mahdollistaa sijainnit tarkasti, samoin kuin liikkuvat esineet, kuten ajoneuvot ja veneet. Se auttaa myös ihmisiä pääsemään helpommin kohteisiinsa ohjaamalla heitä parhaimmilla reiteillä.