Matematiikka

Euklidian geometria

Euklidian geometria

Selitämme, mikä euklidian geometria, sen historia, elementit ja annamme useita esimerkkejä

Alexandrian ja sen elementtien euklidi, kirjoittanut Jusepe de Ribera, viereinen, kaksi ei -rinnakkaista linjaa ja linja, joka leikkaa ne, jotka kuvaavat viidennen postulaatin. Lähde: Wikimedia Commons.

Mikä on euklidian geometria?

Se Euklidian geometria Se on se, jota hallitsevat ne postulaatit Euclid de Alejandría, kreikkalainen geometri, joka asui kohti 300.C, jonka kunniaksi tämä kurinalaisuus on nimetty, koska se oli ensimmäinen systemaattisesti.

Tämä matematiikan haara tutkii linjojen, lentojen, kulmien ja geometristen hahmojen, kuten monikulmioiden, kehysten ja muiden kartiomien, ominaisuuksia. Siksi sen merkitys tieteessä ja tekniikassa, jonka kehitys sai aikaan merkittävästi.

Toisaalta euklidinen geometria oli ensimmäinen tarkka tiede, koska sen kanssa alkoi tieteen systemaation polku, samoin kuin logiikan käytön osoittamiseen muutamasta aksioomasta lukuisia ehdotuksia, joita kutsutaan lauseiksi, ominaisuuksien kuvaamiseksi, ominaisuuksien kuvaamiseksi. geometriset objektit.

Historia

Geometrialla on pitkä historia, koska ihmiskunnan kiinnostus siinä on hyvin vanha ja euklidisen geometrian keskusakseli on työ Kohteet, Alexandrian viisasta euklidista, Egyptissä sijaitsevasta kaupungista ja joka asui neljännellä vuosisadalla.C.

Tuolloin lukuisten lukujen ja geometristen kappaleiden tärkeimmät ominaisuudet olivat tiedossa. Geometriasta oli laajaa tietoa, mutta kaikki oli empiiristä ja puuttui systemaattisointia.

Sitten Egyptin kuningas Ptolemaiosta ja uskoi jo kuuluisan euklidiopettajan, jonka koulu oli Alexandriassa, järjestämään kaikki tähän mennessä käytettävissä olevat matemaattiset ja geometriset tiedot, mukaan lukien lauseet ja kiinteistöt.

Euclides pääsi töihin ja hänen opetuslapsiensa vieressä kirjoitti työelementinsä, jotka hän jakoi kolmeentoista kirjaan, lukuina. Tästä työstä tulee viite geometrialle tuleville sukupolville.

Voi palvella sinua: peräkkäiset johdannaiset

Euclid -elementit

Elementtien sisältö on järjestetty seuraavasti:

  • Kirjoissa I - IV litteä geometria kehittyy.
  • Kirjoissa V ja minä näin suhteellisuusteorian.
  • IX -kirjat on omistettu aritmetiikoille.
  • Kirjassa X näkyy koettavuus,
  • Avaruuden geometria kirjoissa xi - xiii.

Euklidinen geometria oli perusta monille takaosan geometriselle kehitykselle, ja sitä opetetaan parhaillaan kaikissa maailman kouluissa.

Sillä on myös hyve, että se on ensimmäinen työ, joka sisältää loogiseen päättelyyn perustuvia huolellisia mielenosoituksia, ja myös johdonmukaisuus tuon ajan geometrisen ja matemaattisen tiedon runkoon.

Euklidisen geometrian peruselementit

Euklidinen geometria on rakennettu neljän peruselementin ympärille, jotka on kuvattu elementtien I kirjassa:

  1. Täplä
  2. Suoraan
  3. Tasainen
  4. Tilaa

1. Täplä

Eräs täplä Siinä puuttuu mitat tai osat ja se erotetaan toisesta kohdasta yksinkertaisesti sen sijainnin mukaan. Jos kaksi pistettä A ja B ovat erilaisia, se johtuu siitä, että niillä on erilaiset sijainnit, jotka on merkitty hyvin tunnettujen kartesian koordinaattien (x, y) kautta, jos piste on tasossa tai koordinaatit (x, y, z) Jos on avaruudessa.

On huomionarvoista, että Cartesian järjestelmä ei ole osa Kohteet Euclid, mutta ilmestyi paljon myöhemmin 1600 vuoden aikana ja johtuu René Descartesista.

2. Suoraan

Se suoraan Se on ääretön pisteiden kokoelma, ja sillä on vain pituus, ei leveys. Osa siitä vedetään yleensä, nuolet molemmat huomauttavat, että viiva jatkuu toistaiseksi.

3. Tasainen

Eräs tasainen Se on rajoittamaton pinta, joten siinä on kaksi ulottuvuutta ja josta osa on edustettuna neliön tai suorakulmion avulla.

Tasossa on siellä monia geometrisia hahmoja, kuten viivat, avoimet ja suljetut käyrät ja monikulmiot, muun muassa.

Voi palvella sinua: yleinen yhtälö linjasta, jonka kaltevuus on yhtä suuri kuin 2/3

4. Tilaa

Lopuksi on tilaa Kolmen ulottuvuudellaan kykenevä koteloon kaikki kohdat. Se sisältää tasot ja geometriset kappaleet, joille on ominaista niiden tilavuus, kuten polyhedra, pallot ja muut.

Näitä voidaan pitää euklidisen geometrian perusmääritelminä, mutta näiden lisäksi Euclides tarjoaa heidän työssään noin 150 vaihtelevaa määritelmää.

Yleiset käsitteet

Ne koostuvat ilmeisistä ja intuitiivisista tosiasioista, jotka eivät kuulu oikein geometrian laajuuteen ja joita käytetään käsitteiden kehittyessä. Ne viittaavat "asioihin" erittäin laajassa tilanteessa:

  1. Asiat samat jotain muuta, ne ovat samat toistensa kanssa.
  2. Jos asiat lisätään toiseen asioihin, ja kaikki ne ovat samat, mitkä tulokset ovat myös samoja.
  3. Jos yhtäläiset asiat varastetaan, loput ovat myös samat.
  4. Kun asiat vastaavat toisiaan, se johtuu siitä, että ne ovat samoja.
  5. Koko on aina suurempi kuin osapuolet, jotka on otettu erikseen.

Euklidisen geometrian postulaatit

Postulaatit tai aksioomit ovat yksinkertaisia ​​lausuntoja, joita pidetään todellisina ja ilmeisinä, joten ne eivät vaadi esittelyä.

Ne muodostavat perustan euklidian ja euklidin geometrialle viisi kirjaan I:

  1. Ole kaksi eri pistettä ja B, on vain yksi linja, joka kulkee niiden läpi, ts. Kaksi pistettä määrittää linjan.
  2. Mikä tahansa suoraviivainen segmentti voidaan laajentaa määräämättömäksi ajaksi, jotta jokainen segmentti kuuluu linjalle.
  3. Jos sinulla on kaksi eri pistettä tai A.
  4. Kaikki suorat kulmat ovat yhdenmukaisia ​​keskenään.
  5. Kun otetaan huomioon viiva ja kohta P, joka ei kuulu siihen, se on aina mahdollista.

Viimeinen postulaatti, etenkin alkuperäisessä versiossaan, ei näytä niin yksinkertaiselta kuin muut. Se toteaa, että:

Voi palvella sinua: Heptagon

”Jos suora viiva, joka putoaa kahteen muuhun linjaan, tekee kahdesta sisäkulmasta samalla puolella alle kaksi suoraa kulmaa, sanottuna suorat linjat, laajalle levinnyt määräämättömäksi ajaksi, ne ovat (leikkaus) sivulla, jolla pienet kulmat ovat Kaksi suoraa kulmaa ".

Toisin sanoen alun perin postulaatti 5 vahvistaa tilan siten, että kaksi viivaa ei ole yhdensuuntainen. Mutta on selkeämpää, kun se on kirjoitettu siten, että se kuvaa päinvastaista, toisin sanoen linjojen rinnakkaisuus.

Esimerkkejä euklidisen geometriasta

Esimerkki 1

On olemassa kolme erilaista pistettä, merkitty kirjaimilla A, B ja C.

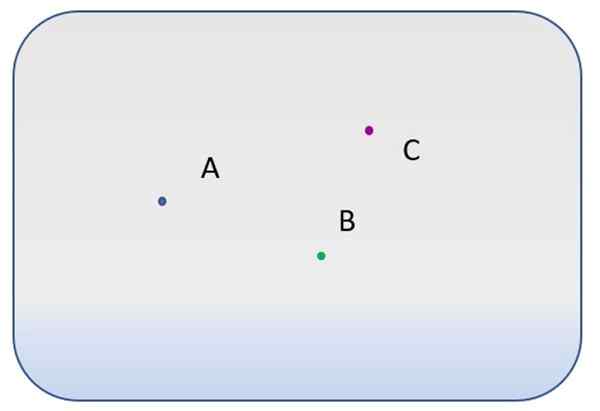
  1. Kuinka monta eri linjaa käy läpi pisteen a?
  2. Ja kuinka monta voidaan piirtää pisteiden A ja B väliin? Ja A: n ja C: n välillä?
  3. Onko mahdollista piirtää viiva, johon pisteet A, B ja C?

Vastaa

Postulaatin I mukaan äärettömät suorat viivat voidaan piirtää A: n läpi, koska viivan määrittämiseksi tarvitaan kaksi pistettä.

Vastaus b

Entre a ja b voidaan piirtää vain viiva. Ja myös A: n välillä.

Vastaus C

Ei ole mahdollista, että linja sisältää A, B ja C samanaikaisesti.

Esimerkki 2

Sitä pyydetään rakentamaan askel askeleelta tasapainon kolmio (kaikki sen sivut ovat yhtä suuret), tietäen yhden sen sivuista, mikä on AB -segmentti ja osoittaa jokaisessa vaiheessa postulaatin tai yleisen käsitteen, jota käytetään rakenteessa.

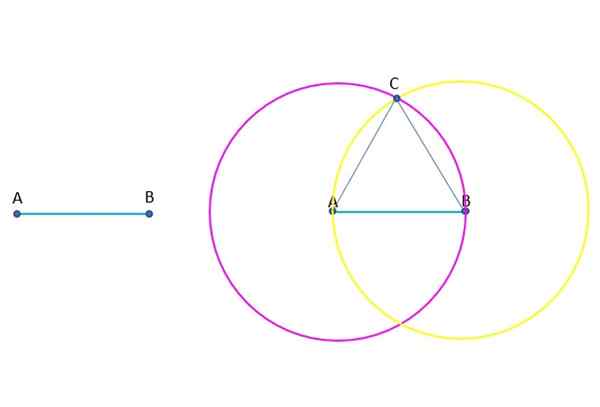ABC: n tasapainon kolmion rakentaminen. Lähde: f. Zapata.

Vastaus

Vaihe 1

Piirros, jonka keskipiste on A ja Radio AB, vedetään. Tämä on aina mahdollista, postulaatin III mukaan.

Vaihe 2

Toinen ympärysmitta B: n ja Radio AB: n keskustan kanssa on piirretty, ja postulaatti III sovelletaan uudelleen.

Vaihe 3

Molemmat kehät, joilla on sama säde, leikataan pisteessä C. Nyt voit piirtää segmenttejä, jotka yhdistävät c: n vastaavasti A: n ja B: n kanssa, postulaatin i mukaan.

Nämä segmentit ovat kehän radioita, ja siksi AC: n ja BC: n mittaukset ovat yhtä suuret kuin AB, yleisen käsitteen 1 mukaan. Sitten ABC -kolmio on tasapainossa.