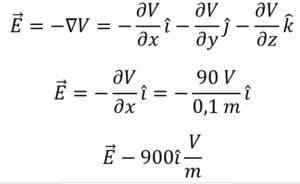Potentiaalinen kaltevuus

Mikä on potentiaalinen kaltevuus?

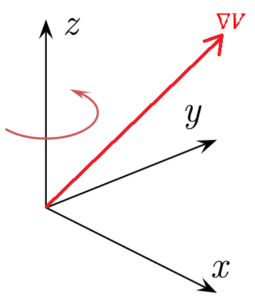
Hän Potentiaalinen kaltevuus Se on vektori, joka edustaa sähköpotentiaalin muutossuhdetta suhteessa Cartesian koordinaattijärjestelmän jokaisella akselilla. Siten potentiaalinen gradienttivektori osoittaa osoitteen, jossa sähköpotentiaalin valuuttakurssi on suurempi etäisyydestä riippuen.

Mahdollinen gradienttimoduuli puolestaan ​​heijastaa tietyssä suunnassa sähköpotentiaalin vaihtelun muutosnopeutta. Jos tämän arvoa on tietoa jokaisessa alueellisessa alueella, sähkökenttä voidaan saada potentiaalisesta kaltevuudesta.

Sähkökenttä määritellään vektoriksi, jolla on tietty suunta ja suuruus. Kun määritetään suunta, johon sähköpotentiaali pienenee nopeammin - se on vertailupiste - ja jakamalla tämä arvo kulkevalla etäisyydellä, sähkökentän suuruus saadaan.

Potentiaalisen kaltevuuden ominaisuudet

Mahdollinen gradientti on vektori, jonka erityiset alueelliset koordinaatit hajoavat, joka mittaa sähköpotentiaalin ja mainitun potentiaalin kuljettaman matkan välistä muutosta. 

Sähköpotentiaalin gradientin merkittävimmät ominaisuudet on yksityiskohtaisesti esitetty:

1- Mahdollinen kaltevuus on vektori. Siksi sillä on tietty suuruus ja suunta.

2- Koska potentiaalinen gradientti on avaruudessa oleva vektori, siinä on X (leveys), y (korkea) ja z-akselit (syvyys), jos Cartesian koordinaattijärjestelmä otetaan referenssinä.

Voi palvella sinua: Puuttuva käyttöjärjestelmä: Mitä se tarkoittaa ja miten se ratkaista

3- Tämä vektori on kohtisuorassa laitteen pinnan suhteen siinä kohdassa, jossa sähköpotentiaali arvioidaan.

4- Potentiaalinen gradienttivektori on suunnattu sähköisen potentiaalin funktion maksimaalisen vaihtelun suuntaan missä tahansa pisteessä.

5- Potentiaalinen gradienttimoduuli on yhtä suuri kuin sähköpotentiaalin funktion johdannainen suhteessa karteesian koordinaattijärjestelmän kunkin akselin suuntaan.

6- Mahdollisella kaltevuudella on nollaarvo paikallaan olevissa kohdissa (maksimiarvo, minimi- ja tuolipisteet).

7- Kansainvälisissä yksiköissä (SI) potentiaaliset gradientin mittausyksiköt ovat voltteja/metriä.

8- Sähkökentän suunta on sama, jossa sähköpotentiaali vähentää sen suuruutta nopeammin. Mahdolliset gradienttipisteet puolestaan ​​suuntaan, johon potentiaali lisää sen arvoa suhteessa sijainnin muutokseen. Sitten sähkökentällä on sama arvo potentiaalisesta kaltevuudesta, mutta vastakkaisella merkinnällä.

Kuinka laskea se?

Ero sähköpotentiaalissa kahden pisteen välillä (piste 1 ja piste 2) annetaan seuraavalla lausekkeella:

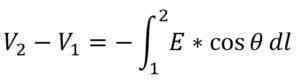
Missä:

• V1: Sähköpotentiaali kohdassa 1.
• V2: Sähköpotentiaali kohdassa 2.
• E: Sähkökentän suuruus.
• Ѳ: Kulma mitatun sähkökenttävektorin kaltevuus suhteessa koordinaattijärjestelmään.

Ilmaisemalla tämä kaava eri tavalla, seuraavat seuraavat:

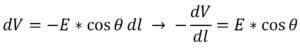
E*cos (ѳ) -kerroin viittaa sähkökenttäkomponentin moduuliin DL: n suuntaan. Olkoon l referenssitason vaakasuora akseli, sitten cos (ѳ) = 1, kuten tämä:

Voi palvella sinua: tekniikka

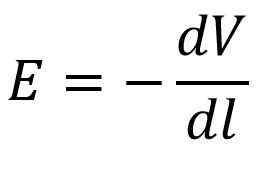
Jäljempänä sähköpotentiaalin variaation (DV) ja kulkevan matkan (DS) variaation välinen osuus on potentiaalinen gradienttimoduuli mainitulle komponentille. 

Sieltä seuraa, että sähköpotentiaalin gradientin suuruus on yhtä suuri kuin tutkimusosoitteen sähkökentän komponentti, mutta päinvastoin.

Koska todellinen ympärist.

Kun sähkökenttävektori hajoaa kolmessa suorakulmaisessa komponentissa, sinulla on seuraavat:

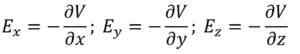
Jos tasolla on alue, jolla sähköpotentiaalilla on sama arvo, tämän parametrin osittainen johdannainen kunkin Cartesian koordinaatin suhteen on mitätön.

Siten laitteiden pisteissä sähkökentän voimakkuudella on nolla suuruus.

Lopuksi, potentiaalinen gradienttivektori voidaan määritellä täsmälleen samaksi sähkökenttävektoriksi (suuruutena), vastakkaisella merkillä. Siksi sinulla on seuraavat:

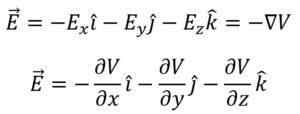
Esimerkki

Edellisistä laskelmista sinun on:

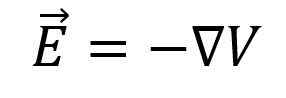
Ennen sähkökentän määrittämistä potentiaalisesta gradientista riippuen tai päinvastoin, suuntaan kasvavan suunta on kuitenkin määritettävä ensin.

Tämän jälkeen määritetään sähköisen potentiaalin vaihtelun ja kulkevan nettoetäisyyden variaatio.

Tällä tavalla saadaan liittyvän sähkökentän suuruus, mikä on yhtä suuri kuin potentiaalisen gradientin suuruus kyseisessä koordinaatissa.

Se voi palvella sinua: 23 etuja ja haittoja verkossa

Harjoittele

Seuraavassa kuvassa on kaksi rinnakkaista levyä.

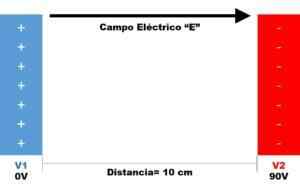
Vaihe 1

Kartesian koordinaattijärjestelmän sähkökentän kasvun osoite määritetään.

Sähkökenttä kasvaa vain vaakasuunnassa, kun otetaan huomioon rinnakkaiset levyjä. Tämän seurauksena on mahdollista päätellä, että Y -akselin ja z -akselin potentiaalisen gradientin komponentit ovat nollaa.

Vaihe 2

Kiinnostustiedot syrjitään.

• Potentiaaliero: DV = V2 - V1 = 90 V - 0 V => DV = 90 V.
• Etäisyysero: dx = 10 senttimetriä.

Kansainvälisen yksikköjärjestelmän mukaisesti käytettyjen mittausyksiköiden yhdenmukaisuuden takaamiseksi suuruudet, joita sinänsä ei ilmaista. Siten 10 senttimetriä on 0,1 metriä ja lopuksi: dx = 0,1 m.

Vaihe 3

Potentiaalisen gradienttivektorin suuruus lasketaan tarvittaessa.