Polynomin aste, jolla se määritetään, esimerkkejä ja harjoituksia

Hän polynomin aste sisään eräs Muuttuja annetaan termillä, joka suurella eksponentilla on, ja jos polynomilla on kaksi tai useampia muuttujia, Sitten aste määritetään kunkin termin eksponenttien summan perusteella, polynomi -olennon päämäärä.

Katsotaanpa kuinka määrittää polynomin aste käytännöllisellä tavalla.

Kuvio 1. Kuuluisa Einstein -yhtälö energialle E on absoluuttinen luokan 1 monomi. Lähde: Piqsels.

Oletetaan, että polynomi p (x) = -5x + 8x³ + 7 - 4x². Tämä polynomi on muuttujaa, tässä tapauksessa se on muuttuja x. Tämä polynomi koostuu useista termeistä, jotka ovat seuraavat:

-5x; 8x³; 7; - 4x²

 Valitaan neljästä termistä, joiden eksponentti on suurempi, tämä termi on:

8x³

Ja nyt mikä on eksponentti? Vastaus on 3. Siksi p (x) on luokan 3 polynomi.

Jos kyseisellä polynomilla on useampi kuin yksi muuttuja, niin aste voi olla:

-Absoluuttinen

-Suhteessa muuttujaan

Absoluuttinen aste selitetään alussa: kunkin termin eksponenttien lisääminen ja suurimman valitseminen.

Toisaalta polynomin aste jonkin muuttujan tai kirjaimen suhteen on suurin arvo, joka on mainittu kirje,. Asia on selkeämpi esimerkkien ja seuraavien osioiden ratkaistujen harjoitusten kanssa.

[TOC]

Esimerkkejä polynomin luokasta

Polynomit voidaan luokitella tutkinnon mukaan, jotta ne voivat olla ensimmäisen asteen, toisen luokan, kolmannen luokan ja niin edelleen. Kuvion 1 esimerkissä energia on ensimmäisen asteen monomiaalinen massa.

Voi palvella sinua: Yhteydet: Yhteydet hahmot, kriteerit, esimerkit, harjoitukset

On myös tärkeää huomata, että polynomilla on termien lukumäärä on yhtä suuri kuin aste plus 1. Niin:

-Ensimmäisen asteen polynomeilla on 2 termiä: a₁x + a_jompikumpi

-Toisella -asennuksen polynomilla on 3 termiä: a₂x² + -lla₁x + a_jompikumpi

-Kolmannen asteen polynomilla on 4 termiä: a₃x³ + -lla₂x² + -lla₁x + a_jompikumpi

Ja niin edelleen. Huomaavainen lukija on havainnut, että aikaisempien esimerkkien polynomit on kirjoitettu vähenevällä tavalla, ts.

Seuraavassa taulukossa esiintyy erilaisia ​​polynomeja, sekä yhdestä ja useista muuttujista että niiden vastaavista absoluuttisista asteista:

pöytä 1. Esimerkkejä polynomeista ja niiden asteista

Polynomi-	Aste
3x4+5x3-2x+3	4
7x3-2x2+3x-6	3
6	0 -
X-1	1
x5-bx4+Abx3+Ab3x2	6
3x3ja5 + 5x2ja4 - 7xy2 + 6	8

Kahdella viimeisellä polynomilla on useampi kuin yksi muuttuja. Termi, jolla on suurin absoluuttinen tutkinto, on eronnut lihavoituna, joten lukija tarkistaa tutkinnon nopeasti. Tärkeää muistaa, että kun muuttujalla ei ole kirjallista eksponenttia, ymmärretään, että mainittu eksponentti on yhtä suuri kuin 1.

Esimerkiksi näkyvällä termillä Ab³x² Muuttujia on kolme, nimittäin: -lla, b - ja x. Siinä vaiheessa, -lla Se on kohonnut arvoon 1, eli:

a = a¹

Siksi Ab³x² = a¹b -³x²

Koska B: n eksponentti on 3 ja X on 2, seuraa heti, että tämän termin aste on:

1+3+2 = 6

Ja se on polynomin absoluuttinen aste, koska millään muulla termillä ei ole suurempaa astetta.

Menettely polynomien kanssa

Kun työskentelet polynomien kanssa

-Järjestetään etusijapolynomi vähenevässä mielessä. Tällä tavalla termi, jolla on korkein luokka, on vasemmalla ja se on alhaisin oikealle.

Voi palvella sinua: Endecagon

-Vähennä samanlaisia ​​termejä, menettely, joka koostuu kaikkien tasa -arvoisten muuttujien ja asteen termien lisäämisestä, jotka ovat ekspression algebrallisesti.

-Tarvittaessa polynomit valmistuvat, välitteet, joiden kerroin on 0, jonkin verran eksponentin kanssa.

Tilaa, vähennä ja suorita polynomi

Kun otetaan huomioon polynomi p (x) = 6x² - 5x⁴- 2x+3x+7+2x⁵  - 3x³ + x⁷ -12 Pyydetään tilaamaan vähenevän, vähentävät samanlaisia ​​ehtoja, jos niitä on, ja täydentävät puuttuvat ehdot, jotka ovat tarkkoja.

Ensimmäinen asia, jota etsitään, on termi tärkeimmän eksponentin kanssa, joka on polynomin aste, joka osoittautuu:

x⁷

Siksi p (x) on luokka 7. Sitten polynomi tilataan, aloittaen tällä termillä vasemmalle:

P (x) = x⁷ + 2x⁵ - 5x⁴ - 3x³ + 6x² - 2x+3x+7 -12

Samanlaisia ​​termejä on nyt vähentynyt, jotka ovat seuraavat: - 2x ja 3x toisaalta. Ja 7 ja -12 toisella. Niiden vähentämiseksi kertoimia lisätään algebrallisesti ja muuttuja jätetään muuttumattomaksi (jos muuttuja ei näytä kerroimen vieressä, on muistettava, että x X^{0 -} = 1):

-2x+3x = x

7 -12 = -5

Nämä tulokset korvataan p (x):

P (x) = x⁷ +2x⁵ - 5x⁴ - 3x³ + 6x² + x -5

Ja lopuksi polynomia tutkitaan nähdäkseen, onko eksponentti puuttuva ja voimassa, termi, jonka eksponentti on 6, se puuttuu, siksi se on valmis nollailla:

P (x) = x⁷ + 0x⁶ +2x⁵ - 5x⁴ - 3x³ + 6x² + X - 5

Nyt havaitaan, että polynomialle jätettiin 8 termiä, koska kuten aiemmin sanottiin, termien lukumäärä on yhtä suuri kuin aste + 1.

Polynomin asteen merkitys summassa ja vähentämisessä

Polynomien kanssa voidaan suorittaa summa- ja vähennysoperaatiot, joihin lisätään tai vähennetään vain samanlaisia ​​termejä, jotka ovat sama muuttuja ja sama aste. Jos samanlaisia ​​termejä ei ole, summa tai vähennys jätetään yksinkertaisesti.

Voi palvella sinua: jakava omaisuus

Kun summa tai vähennys on tehty, jälkimmäinen on päinvastaisen summa, tuloksena olevan polynomin aste on aina yhtä suuri tai pienempi kuin suuremman asteen polynomin lisäysaste.

Ratkaisut

- Liikunta ratkaistiin 1

Etsi seuraava summa ja määritä sen absoluuttinen aste:

-lla³- 8Ax²  + x³ + Viides²X - 6ax² - x³ + Kolmas³ - Viides²x - x³ + -lla³+ 14Ax² - x³

Ratkaisu

Se on kahden muuttujan polynomi, joten on kätevää vähentää samanlaisia ​​termejä:

-lla³- 8Ax²  + x³ + Viides²X - 6ax² - x³ + Kolmas³ - Viides²x - x³ + -lla³+ 14Ax² - x³ =

= a³ + Kolmas³ + -lla³ - 8Ax² - 6Ax²+ 14Ax² +Viides²X - 5a²x+ x³- x³- x³- x³ =

= 5a³ - 2x³

Molemmat termit ovat luokka 3 kussakin muuttujassa. Siksi polynomin absoluuttinen aste on 3.

- Liikunta ratkaistiin 2

Ilmaise polynomina seuraavan litteän geometrisen kuvan pinta -ala (kuva 2 vasemmalla). Mikä on tuloksena oleva polynomin aste?

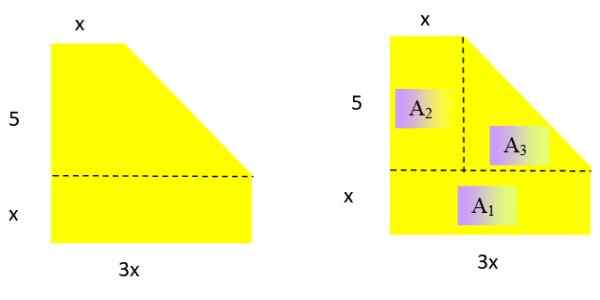Kuva 2. Vasemmalla puolella vuoden lukumäärä ratkaisi 2 ja oikealle, sama luku hajosi kolmella alueella, joiden ilmaisu on tiedossa. Lähde: f. Zapata.

Ratkaisu

Alueena saadun polynomin on oltava luokan 2 muuttuja X. Alueen riittävän lausekkeen määrittämiseksi luku on jaettu tunnetuille alueille:

Suorakulmion ja kolmion alue on vastaavasti: Pohja x korkeus ja Pohja x korkeus /2

-Lla₁ = x . 3x = 3x²; -Lla₂ = 5 . x = 5x; -Lla₃ = 5 . (2x /2) = 5x

Huomautus: Kolmion pohja on 3x - x = 2x ja sen korkeus on 5.

Nyt lisätään kolme saadut lausekkeet, jolloin sinulla on kuvion pinta -ala riippuen x-

3x² + 5x + 5x = 3x² + 10x

Viitteet

1. Baldor, a. 1974. Perusalgebra. Venezuelan kulttuurinen s.-Lla.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Wikilibros. Polynomit. Palautettu: on. Wikibooks.org.
4. Wikipedia. Luokka (polynomi). Palautettu: on.Wikipedia.org.
5. Zill, D. 1984. Algebra ja trigonometria. Mac Graw Hill.