Gravicentro

Mikä on vero?

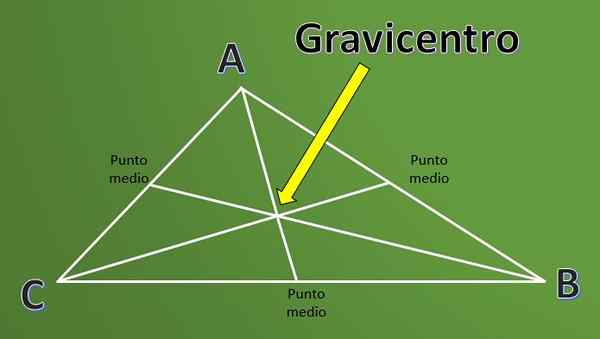
Hän Gravicentro Se on määritelmä, jota käytetään laajasti geometriassa työskennellessään kolmioiden kanssa. Gravicentro -määritelmän ymmärtämiseksi on ensin tarpeen tietää kolmion "väliaine" määritelmä.

Kolmion mediaanit ovat linjasegmentit, jotka alkavat jokaisesta kärkipisteestä ja saavuttavat vastakkaisen puolen keskipisteen kuin mainitulle kärkipisteelle.

Kolmen kolmion mediaanin leikkauspistettä kutsutaan baricentroksi tai sitä kutsutaan myös verotukseksi. Ei riitä vain, että tiedät määritelmän, on mielenkiintoista tietää, kuinka tämä kohta lasketaan.

Baricenterin laskenta

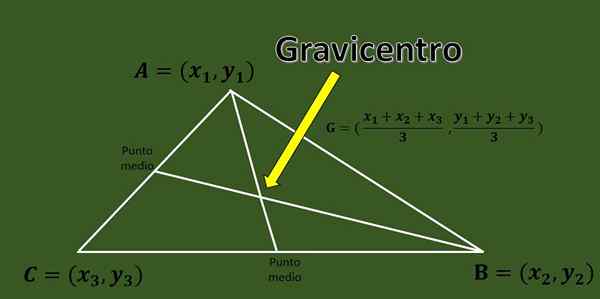
Annetaan ABC -kolmio, jossa on kärkipisteet a = (x1, y1), b = (x2, y2) ja c = (x3, y3), gravicentro on kolmion kolmen mediaanin leikkauspiste.

Nopea kaava, joka sallii kolmion verotuksen laskemisen, sen tiedossa olevien kärkien koordinaatit ovat:

G = ((x1+x2+x3)/3, (y1+y2+y3)/3).

Tämän kaavan avulla voit tietää Gravicentro -sijainnin Cartesian tasossa.

Veron ominaisuudet

Kolmion kolmea mediaania ei ole tarpeen jäljittää, koska vedettäessä kahta heistä käy ilmi, missä verotus on.

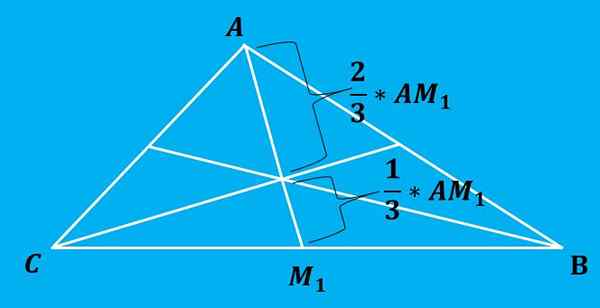
Verotus jakaa jokaisen mediaanin kahteen osaan, joiden osuus on 2: 1, ts. Kunkin mediaanin kaksi segmenttiä on jaettu 2/3: n pituuksien segmenteihin ja 1/3 kokonaispituudesta, sitä suurempi etäisyys on yksi Mitä kärjessä ja esitteen välillä on.

Seuraava kuva kuvaa tätä ominaisuutta paremmin.

Verotuksen laskentakaava on hyvin helppo soveltaa. Tapa saada tämä kaava on laskemalla suorat yhtälöt, jotka kukin mediaani määrittelee, ja löydä sitten näiden viivojen leikkauspiste.

Harjoitukset

Alla on pieni luettelo ongelmista Baricenterin laskemisessa.

1.- Kun otetaan huomioon kärkipisteiden kolmio A = (0,0), B = (1,0) ja C = (1,1), laske vuoden verotus.

Annetusta kaavaa käyttämällä voidaan nopeasti päätellä, että ABC -kolmion gravicentro on:

G = ((0+1+1)/3, (0+0+1)/3) = (2/3, 1/3).

2.- Jos kolmiossa on kärjet a = (0,0), b = (1,0) ja c = (1/2,1), mitkä ovat verotuksen koordinaatit?

Koska kolmion kärkipisteet tunnetaan, verotuksen laskennan kaava sovelletaan. Siksi Gravicentrolla on koordinaatit:

G = ((0+1+1/2)/3, (0+0+1)/3) = (1/2, 1/3).

3.- Laske mahdolliset veronmaksajat tasapainon kolmiolle siten, että kaksi sen kärkipistettä ovat a = (0,0) ja b = (2,0).

Tässä harjoituksessa määritetään vain kaksi kolmion kärkeä. Mahdollisten gracisenterien löytämiseksi kolmion kolmannen kärjen on ensin laskettava.

Koska kolmio on tasapaino ja etäisyys A: n ja B: n välillä on 2, kolmannen kärjen C on oltava A: n ja B: n etäisyydellä 2.

Käyttämällä sitä tosiasiaa, että tasasivuisessa kolmiossa korkeus vastaa mediaania ja käyttämällä myös Pythagoras -lausetta, voidaan päätellä, että kolmannen kärjen koordinaattien vaihtoehdot ovat C1 = (1, √3) tai C2 = (1, 1, 1, 1, - - - √3).

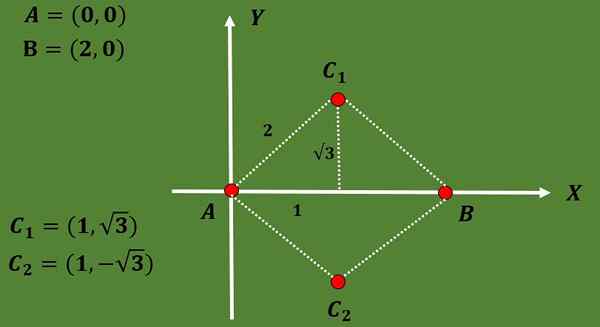
Niin että kahden mahdollisen gravicenterin koordinaatit ovat:

G1 = ((0+2+1)/3, (0+0+√3)/3) = (3/3, √3/3) = (1, √3/3),

G2 = ((0+2+1)/3, (0+0 -√3)/3) = (3/3, -√3/3) = (1, -√3/3).

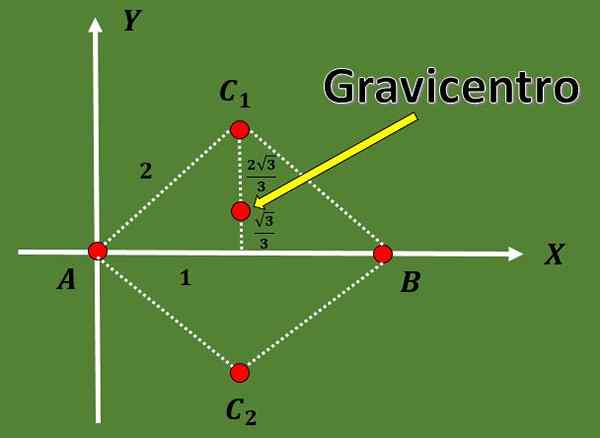
Edellisten tilien ansiosta voidaan myös huomata, että mediaani on jaettu kahteen osaan, joiden osuus on 2: 1.