Hyperbeli

Mikä on hyperbola?

Hyperbola on tason pisteiden joukko siten, että etäisyyksien välisen eron absoluuttinen arvo kahteen kiinteään pisteeseen, nimeltään Spotlights, pysyy vakiona. Tämä pistejoukko muodostaa käyrän kahdella kuvassa 1 havaitun haaran kanssa.

On piste p (x, y), foci f₁ ja f₂ erotettu etäisyys, joka on yhtä suuri kuin 2c. Matemaattinen tapa ilmaista tämä suhde on:

Kuvio 1. Hyperbola, jossa on vaakasuora akseli. Lähde: f. Zapata.

Kaikki hyperbolan kohdat tyydyttävät tämän tilan, joka johtaa hyperbola -yhtälöön, kuten myöhemmin nähdään. Kohdevalojen välistä keskipistettä kutsutaan keskukseksi C ja kuvassa se on samanaikainen piste (0,0), mutta hyperbola voidaan myös siirtyä ja sen keskus vastaa toista koordinaattipistettä C (H, K).

Yläkuviossa X -akseli on hyperbolan polttoakseli, koska siellä on valonheittimiä, mutta voit myös rakentaa sellaisen, jonka fokusakseli on akseli ja akseli.

Hyperbola on osa nimellä tunnetut käyrät kartiomainen, Niitä kutsutaan niin, koska ne voidaan johtaa kartion leikkauksesta, jossa on tasainen osa. Hyperbola saadaan kartion ja tason leikkaamisen yhteydessä, edellyttäen, että se ei kulku kartion kärjen läpi ja kulma, joka muodostaa tason kartion akselin kanssa sama.

Yhdessä vertauksen, kehän ja ellipsin kanssa kartiot tunnetaan muinaisista ajoista lähtien. Pergan kreikkalainen matemaatikko Apollonius (262-190 eKr.) Kirjoitti geometriasopimuksen, jossa hän yksityiskohtaisesti hänen ominaisuutensa ja hän itse antoi heille nimet, joiden kanssa he tuntevat toisensa tähän päivään asti.

Hyperbolan ominaisuudet

Nämä ovat joitain hyperbolan merkittävimmistä ominaisuuksista:

1. Se on litteä käyrä, siksi se riittää antamaan jokaisen siihen kuuluvan pisteen koordinaatit (x, y).
2. Se on myös avoin käyrä, toisin kuin kehä tai ellipsi.
3. Siinä on kaksi haaraa, jotka on järjestetty symmetrisesti.
4. Sekä pystysuuntaista akselia että vaakasuoraa akselia voidaan pitää symmetria -akselina, mutta akselia, jossa valonheittimiä kutsutaan polttoakseli tai pääakseli.
5. Se on symmetrinen suhteessa keskukseen.
6. Hyperbola leikkaa polttoakselin kahdessa pisteessä, nimeltään Kärjet, Siksi fokusakselia kutsutaan joskus todellinen akseli, kun taas toista akselia kutsutaan Kuvitteellinen akseli, Koska sillä ei ole yhteisiä pisteitä hyperbolan kanssa.
7. Hyperbolan keskipiste sijaitsee puolivälissä pisteiden välillä, nimeltään Foci.
8. Se liittyy kahteen hyvin erityiseen linjaan, joita kutsutaan asymptoteiksi, jotka ovat linjoja, joille hyperbola lähestyy, mutta ilman niiden ylittämistä, kun x e y: n arvot ovat erittäin suuria. Asymptotit leikkaavat hyperbolan keskellä.

Voi palvella sinua: Overjektiivitoiminto: Määritelmä, ominaisuudet, esimerkit

Yhtälöt ja kaavat

Hiperbol -yhtälö keskustassa (0,0)

Alussa annetusta määritelmästä alkaen:

Tähän positiiviseen vakioon sitä kutsutaan yleensä 2a: lle ja etäisyys erottaa hyperbolan kärkipisteet: sitten:

Toisaalta DP₁, DP₂ ja 2C ovat kuviossa 1 esitetyn kolmion sivut ja alkuainegeometrialla minkä tahansa kolmion sivujen vähennys on aina pienempi kuin jäljellä olevan sivun neliö. Niin:

Neljäs² < 4c²

JA:

-lla < c

Tämä tulos on hyödyllinen pian.

Etäisyytenä kahden pisteen P välillä₁(x₁,ja₁) Ja p₂(x₂,ja₂) On:

Korvaamalla koordinaatit P (x, y), f₁(-C, 0) ja F₂(C, 0) Se on:

Mikä vastaa:

Neliö molemmissa jäsenissä juurten poistamiseksi ja tavoittamasi ehdot uudelleen järjestämiseksi:

Määrä c² - -lla², mikä on aina positiivinen määrä, koska < c, se la denomina b², Siksi yllä oleva uudelleen kirjoitetaan seuraavasti:

b -²x² - -lla²ja² = a² b -²

Kaikkien termien jakaminen² b -², Se on hyperbola -yhtälö, joka on keskitetty (0,0) vaakasuuntaiseen todelliseen akseliin:

A ja B yli 0. Tätä yhtälöä kutsutaan Hyerbola kanoninen yhtälö ja nimittäjä² Se vastaa aina positiivista osaa.

Hyperbola keskittyy (0,0) ja oikean akselin pystysuoran ollessa muodossa:

Hyperbolan risteykset koordinaattiakselien kanssa

Hyperbolan leikkaukset koordinaattiakselien kanssa tehdään vastaavasti y = 0 ja x = 0 yhtälössä:

Y = 0: lle

x² /² = 1 ⇒ x² = a²

x = ± a

Hyperbola leikkaa X -akseliin kahdessa pisteessä, joita kutsutaan kärkipisteiksi, joiden vastaavat koordinaatit x ovat: x = a y x = -a

X = 0

Se saadaan -ja² /b² = 1, jolla ei ole todellista ratkaisua ja seuraa, että hyperbola ei leikkaa pystysuoraan akseliin.

Hyperbola -yhtälö keskustassa (h, k)

Jos hyperbolan keskipiste on kohdassa C (H, K), sen kanoninen yhtälö on:

Hiperbola -elementit

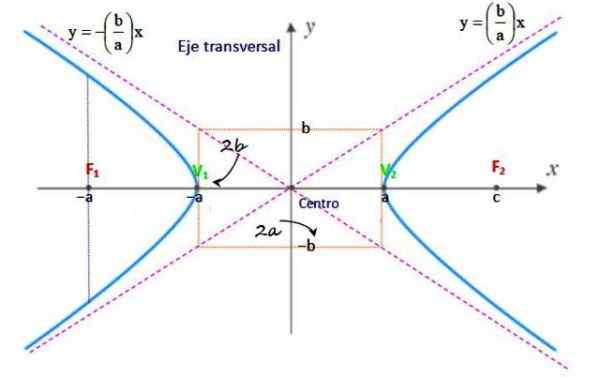Kuva 2. Hiperbola -elementit. Lähde: f. Zapata.

Keskusta

Se on segmentin f keskipiste₁F₂ Ja sen koordinaatit ovat (h, k) tai (x_jompikumpi,ja_jompikumpi-A.

Voi palvella sinua: synteettinen jako

Keskittyä

Ne ovat kaksi kiinteää pistettä f₁ ja f₂ jotka ovat hyperbolan todellisella akselilla, joiden osalta pisteen p (x, y) etäisyyden ero pysyy vakiona. Etäisyys valonheittimien ja hyperbolan keskustan välillä on "C".

Vektoriradio

Tätä kutsutaan pisteen P ja yhden valokeilan väliseksi etäisyydeksi.

Polttomatka

Se on etäisyys, joka erottaa molemmat valonheittimet ja vastaa 2C.

Kärjet

Verkit v₁ ja v₂ Ne ovat pisteitä, joissa hyperbola leikkaa todellisen akselin. Vertex ja hyperbolan keskusta erotetaan etäisyydellä A, siksi kärjessä oleva etäisyys on 2a.

Fokusakseli, pääakseli tai todellinen akseli

Se on akseli, jolla valonheittimet sijaitsevat ja mittaa 2c. Se voidaan sijaita kummassakin kartesia -akselissa ja hyperbola leikkaa sen pisteissä, joita kutsutaan kärkipisteiksi.

Poikittainen akseli, sekundaarinen akseli tai kuvitteellinen akseli

Se on akseli kohtisuorassa polttoakseliin nähden ja mittaa 2b. Hyperbola ei leikkaa sitä, joten sitä kutsutaan myös kuvitteelliseksi akseliksi.

Asymptotit

Ne ovat kaksi riviä, joiden vastaavat vireillä on m₁ = (b/a) ja m₂ = - (b/a), jotka on tarkoitettu hyperbolan keskelle. Käyrä ei koskaan leikkaa näitä viivoja ja tuotetta hyperbolan minkä tahansa pisteen välillä asymptootteihin, se on vakio.

Asymptoottien yhtälöiden löytämiseksi vastaa vain hyperbola -kanonisen yhtälön vasenta puolta arvoon 0. Esimerkiksi hyperbolalle, joka on keskittynyt alkuperään:

Hyberbola suorakulmio

Se on suorakulmio, jonka leveys on etäisyys kärkien 2a ja etäisyyden 2b välillä ja keskittyy hyperbolan keskustaan. Sen rakenne helpottaa hyperbolan manuaalista asettelua.

Suorakulma

Köysi, joka kulkee yhden valonheittimen läpi, kohtisuorassa todelliseen akseliin nähden.

Epäkeskeisyys

Se määritellään osamääräksi polttovälin ja todellisen akselin välillä:

E = c/a

Se on aina suurempi kuin 1, koska C on suurempi kuin A ja vähemmän kuin √2.

Arvo ja osoittaa, onko hyperbola melko suljettu (kapea suorakulmio, pitkänomainen pääakselin suuntaan) vai avoin (leveä suorakulmio, pitkänomainen kuvitteellisen akselin suuntaan).

Suora tangentti hyperbolalle pisteessä P (x₁,ja₁-A

Tangentti viiva hyperbolaan pisteessä P (x₁,ja₁) Se on kyseisen pisteen kahden radiovektorin puoliaja.

Hyperbolalle, jonka pääakseli on yhdensuuntainen X -akselin kanssa, linjan kaltevuus hyperbolalle pisteessä P (x₁,ja₁) annetaan:

Voi palvella sinua: yhdistetyt toiminnot

Ja jos hyperbola on pääakseli yhdensuuntainen Y -akselin kanssa, niin:

Esimerkkejä hyperbolasta

Alfahiukkasten leviäminen ytimellä

Pommittamalla atomi -ytimiä alfahiukkasten kanssa, jotka ovat vain helium -ytimiä, nämä hylätään, koska kaikilla atomiykkeillä on positiivinen varaus. Nämä helium -ytimet ovat dispergoituneita hyperbolisten suuntausten jälkeen.

Aurinkokunnan rungon etenemissuunnitelmat

Kuva 3: Aurinkojärjestelmän planeetat

Aurinkojärjestelmässä esineet liikkuvat painovoiman vaikutuksen alla. Liikkeen kuvaus johtuu differentiaaliyhtälöstä, jossa voima on konservatiivinen ja käänteisesti verrannollinen etäisyyden neliöön. Ja tämän yhtälön ratkaisut ovat mahdollisia suuntauksia, jotka seuraavat esineitä.

Nämä suuntaukset ovat aina kartiomaisia: kehykset, ellipsit, vertaukset tai hyperbolat. Kaksi ensimmäistä ovat suljettuja käyriä, ja näin planeetat liikkuvat, mutta jotkut komeetit ovat edelleen avoimia suuntauksia, kuten vertauksia tai hyperboloja, aurinko sijaitsee yhdessä valokeilassa.

Vähimmäisääni

Kun on olemassa kaksi äänilähdettä, kuten kaksi kaiutinta, jotka säteilevät tasaisesti kaikkiin suuntiin, jotka sijaitsevat suoraa linjaa pitkin, äänenvoimakkuuden minimit (tuhoavat häiriöt) ovat hyperbolassa, jonka pääakseli sanotaan viivalla, ja Spotlights of Of Hyperbola ovat kaiuttimia.

Liikuntaa

Löydä seuraavan hyperbolan elementit: Hyperbolan kärjet, polttoaineet ja asymptotit ja rakenna sen kuvaaja:

Ratkaisu

Tämän hyperbolan keskus osuu samanaikaisesti koordinaattien alkuperän ja sen todellinen akseli on vaakasuora, koska positiivinen fraktio vastaa muuttujaa x.

Hyperbola -puoliaksit ovat:

-lla² = 16 ⇒ A = 4

b -² = 4 ⇒ B = 2

Tällä tavoin keskimmäinen suorakulmio on 4 yksikköä leveä ja 2 yksikköä korkea. Muistaa, että edellä mainittiin, että c² - -lla² = b² , niin:

c² = a² + b -² ⇒ c² = 16 + 4 = 20

Siksi fokus puolipäästö on:

C = √20 = 2√5

Ja polttoaineet ovat koordinaattipisteissä f₁ (-2√5.0) ja f₂ (2√5.0).

Asymptoottien rinteet ovat:

m = ± (b/a) = ± (2/4) = ± 0.5

Siksi kunkin vastaavat yhtälöt ovat:

ja₁ = 0.5x; ja₂ = -0.5x

Hyperbola pystyy helposti kuvaamaan online -ohjelmistojen, kuten geogebra, kautta:

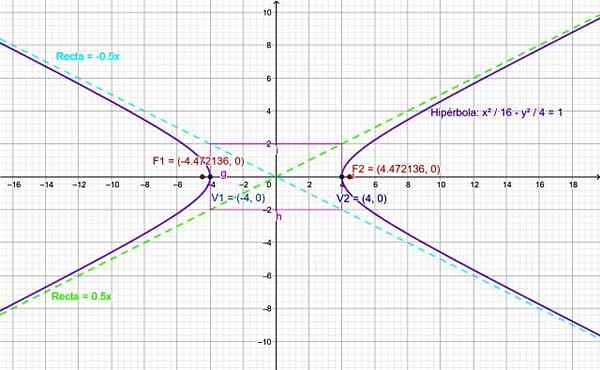Kuva 4. Kaavio harjoituksen hyperbolalle ratkaistu. Lähde: f. Zapata.

Viitteet

1. Fiscalab. Hyperbola -yhtälö. Toipunut: fisikab.com
2. Hoffman, J. Matematiikan aiheiden valinta. Nide 2.
3. Stewart, J. 2006. Precculment: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.
4. Maailmankaikkeuden kaavat. Hyperbola. Toipunut: UniversOformulat.com
5. Zill, D. 1984. Algebra ja trigonometria. McGraw Hill.