ICosagono

Mikä on ICOGON?

Eräs Icosagono tai isodecagon Se on monikulmio, jolla on 20 puolta. Monikulmio on tasainen kuva, joka on muodostettu rajallisella linjasegmenttien sekvenssillä (yli kaksi), jotka sulkevat tason alueen.

Jokaista linjasegmenttiä kutsutaan sivuksi ja kunkin sivuparin leikkauspistettä kutsutaan kärkipisteeksi. Sivujen lukumäärän mukaan monikulmikoneet vastaanottavat tiettyjä nimiä.

Yleisimpiä ovat kolmio, nelikulmainen, Pentagon ja Hexagon, joilla on vastaavasti 3, 4, 5 ja 6 sivua, mutta jotka voidaan rakentaa haluamien sivujen lukumäärän kanssa.

Icogonin ominaisuudet

Alla on joitain monikulmioiden ominaisuuksia ja niiden käyttö ICOGONissa.

1- luokittelu

ICOSGONO, joka on monikulmio, voidaan luokitella tavallisiksi ja epäsäännöllisiksi, missä tavallinen sana viittaa tosiasiaan, että kaikilla puolilla on sama pituus ja sisäkulmat mittaavat kaikki samat; Muuten sanotaan, että icosagon (monikulmio) on epäsäännöllinen.

2- Isodecagon

Tavallista iCosgonia kutsutaan myös tavalliseksi isodogoniksi, koska tavallisen ICOSGON -gaugen saamiseksi se, mitä pitäisi tehdä, on bisekaari (jaa kahteen yhtä suureen osaan) tavallisen dekaanin kummallakin puolella (10 sivua monikulmio).

3- kehä

Säännöllisen monikulmion kehän "P" laskemiseksi sivujen lukumäärä kerrotaan kummankin puolen pituudella.

ICOGONin erityistapauksessa kehä on yhtä suuri kuin 20xl, missä "l" on kummankin puolen pituus.

Esimerkiksi, jos sinulla on säännöllinen 3 cm: n sivu icosagon, sen kehä on yhtä suuri kuin 20x3cm = 60 cm.

On selvää, että jos isokagoni on epäsäännöllinen, aikaisempaa kaavaa ei voida soveltaa.

Tällöin 20 puolta on lisättävä erikseen kehän saamiseksi, ts. Käymä “P” on yhtä suuri kuin ∑li, I = 1,2,…, 20.

4- diagonaali

Polygonilla olevien D-diagonaalien lukumäärä on yhtä suuri kuin N (N-3)/2, missä n edustaa sivujen lukumäärää.

ICOGONin tapauksessa sen on oltava d = 20x (17)/2 = 170 diagonaalia.

5- Sisäisten kulmien summa

On kaava, joka auttaa laskemaan tavallisen monikulmion sisäkulmien summa, jota voidaan käyttää tavalliseen ICOSGONiin.

Kaava koostuu 2 monikulmion sivujen vähentämisestä ja sitten tämän lukumäärän kertominen 180º: lla.

Tapa, jolla tämä kaava saadaan, on, että voimme jakaa N-sivujen monikulmion N-2-kolmioihin ja käyttämällä sitä tosiasiaa, että kolmion sisäkulmien summa on 180º, kaava saadaan.

Seuraavassa kuvassa on kuvattu kaava tavallisen Enegonin (9 -osainen monikulmio) kaava.

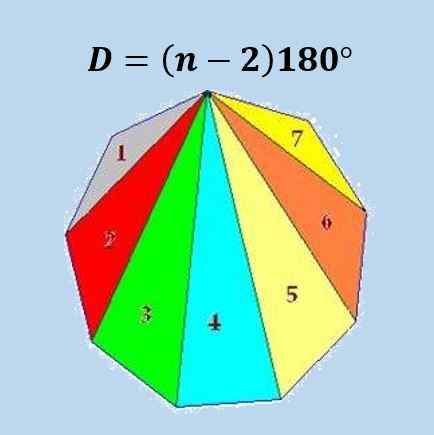
Etukaavaa käyttämällä saadaan, että minkä tahansa icosagonin sisäkulmien summa on 18 × 180º = 3240º tai 18π.

6- Alue

Säännöllisen monikulmion alueen laskemiseksi on erittäin hyödyllistä tietää Apotemin käsite. Apotheem on kohtisuora viiva, joka menee tavallisen monikulmion keskustasta minkä tahansa sivun keskipisteeseen.

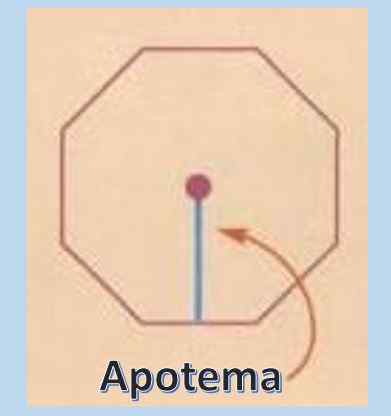
Kun apoteemin pituus on tiedossa, tavallisen monikulmion pinta -ala on A = PXA/2, missä "P" edustaa kehää ja "A" Apotheme.

Tavallisen icosagonin tapauksessa alueellesi on A = 20xlxa/2 = 10xlxa, missä "l" on kummankin puolen pituus ja "a" sen apotheme.

Toisaalta, jos sinulla on epäsäännöllinen N-sivujen monikulmio, sen alueen laskemiseksi, monikulmio on jaettu N-2-tunnettuihin kolmioihin, niin näiden N-2-kolmioiden pinta-ala on laskettu ja lopulta kaikki nämä ovat lisättyjä alueita.

Edellä kuvattu menetelmä tunnetaan monikulmion triangulaationa.

Viitteet

1. Geometriaelementit: lukuisilla harjoituksilla ja kompassin geometrialla. Medellinin yliopisto.
2. Iger. (S.F.-A. Matematiikka ensimmäisen lukukauden Tacaná. Iger.