Matemaattinen tasa -arvo
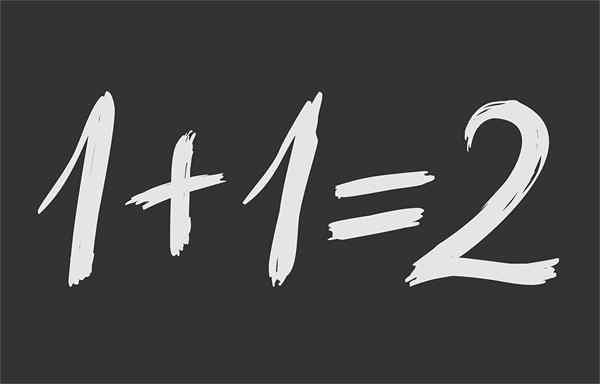
- 3582
- 107
- Alonzo Kirlin
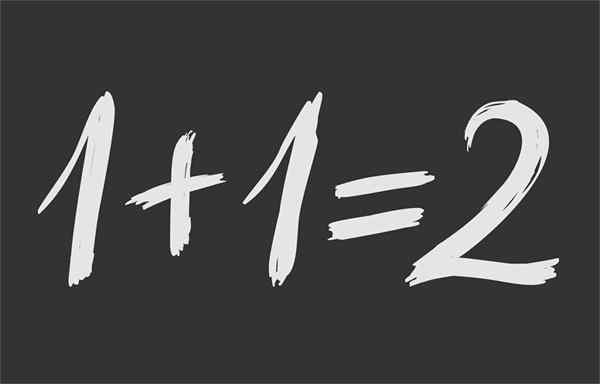 Kuvio 1.- Matemaattinen tasa -arvo varmistaa, että 1 + 1 on sama 2
Kuvio 1.- Matemaattinen tasa -arvo varmistaa, että 1 + 1 on sama 2 Mikä on matemaattinen tasa -arvo?
Matemaattinen tasa -arvo varmistaa, että kaksi lauseketta ovat samat tai erilaiset, ne ovat täysin vastaavia. Nämä lausekkeet voivat olla monipuolisia luonnetta, esimerkiksi numeroita, kirjaimia, jotka symboloivat määriä tai suuruuksia, numeroiden ja kirjaimien yhdistelmiä, matriiseja ja paljon muuta.
Matemaattisen kielen tasa -arvon merkitsemiseen käytetty symboli on kaksi rinnakkaista ja vaakasuoraa viivaa, jotka painetussa tekstissä on hyvin tunnettu symboli "=". Esimerkiksi, jos sinulla on kolme omenaa, voit kirjoittaa seuraavan tasa -arvon:
Omenoiden lukumäärä = 3
Lause "omenoiden lukumäärä" on vasemman jäsen ja numero 3 on tasa -arvon oikealla puolella.
Koska on mahdollista kirjoittaa numeerisia määriä eri tavoin, tasa -arvoa käytetään niiden merkitsemiseen. Ottaen tietyn tapauksen havainnollistaakseen, on useita tapoja kirjoittaa numero 4, lukuun ottamatta selvimpiä, joka on 4 = 4, seuraava voidaan kirjoittaa matemaattisen tasa -arvon kautta:
2 + 2 = 4
6 - 2 = 4
8 ÷ 2 = 4
2 × 2 = 4
22 = 4
Tässä esitetty tasa -arvo on totta, mutta tasa -arvo ei välttämättä ole, esimerkiksi 10 + 5 = 20 on väärä, koska 10 + 5 = 15.
Varmasti lukija tietää muita tapoja kirjoittaa numero 4. Huomaa, että tasa -arvon kummallakin puolella olevat lausekkeet voivat olla esimerkiksi numeroita, sanoja, kirjaimia, jotka symboloivat määriä tai muita symboleja:
x + 1 = 7
-lla2B - 1 = xy
f (x) = 2x2
Matemaatikot eivät aina käyttäneet tasa -arvosymbolia, joten vanhat matematiikkasopimukset olivat erittäin laajoja.
Se johtuu matemaatikoista ja tohtorista Robert Remement (1510-1558), syntynyt Walesissa, tasa-arvosymbolin "=" luominen, niin tuttu kaikille tänään. Muista, että ilmeisesti kyllästynyt kirjoittamaan aina lause "aivan kuten" yhdessä hänen matematiikkasopimuksistaan, hän päätti lyhentää hänen tilalleen sukulaisia rinnakkaisia raitoja.
Voi palvella sinua: Pentagonaalinen prisma: Ominaisuudet, osat, kärjet, reunat, tilavuusMatemaattisen tasa -arvon ominaisuudet
Seuraavat ominaisuudet sallivat työskennellä oikein matemaattisen tasa -arvon kanssa. Ne ovat aksiomaattisia, joten ne eivät vaadi esittelyä:
1.- Heijastava ominaisuus
Tämä ominaisuus osoittaa, että mikä tahansa määrä on yhtä suuri kuin itse. Erityisesti, koska mikä tahansa luku on yhtä suuri kuin itsessään, voidaan kirjoittaa:
5 = 5
36.35 = 36.35
Jos määrä on kirjaimellinen tai se on kirjaimien ja numeroiden yhdistelmä, se on myös yhtä suuri kuin itse:
3x = 3x
-lla2BC-1 = a2BC-1
2.- Symmetrian ominaisuus
Tasa -arvon molemmin puolin olevat määrät tai jäsenet voidaan vaihtaa ilman menetettyä pätevyyttä. Eli jos "=" -symbolin vasemmalla puolella on kirjoitettu oikealle ja mikä oikealla on vasemmalle, se on sama tasa -arvo.
Esimerkiksi lauseke 5 + 2 = 7 vastaa tätä: 7 = 5 + 2. Samalla tavalla:
12 + 8 = 20; 20 = 12 + 8
x + 1 = 3; 3 = x + 1
x - z = y; y = x - z
3.- Transitiivinen ominaisuus
Tämä ominaisuus viittaa tasa -arvon vastaavuuteen. Jos kahdella tasa -arvolla on yhteinen jäsen, niin he ovat myös samat, koska yleensä:
Jos “x = y” ja “y = z”, niin x = z
Tämän ominaisuuden havainnollistamiseksi harkitse näitä kahta numeerista yhtäläisyyttä: 2 + 2 = 4 ja 6 - 2 = 4. Koska molemmat ovat yhtä suuret kuin 4 (heillä on yhteinen jäsen), seuraavat voidaan kirjoittaa menettämättä mitään pätevyyttä:
2 + 2 = 6 - 2
Toinen esimerkki, tällä kertaa kirjaimilla:
Kyllä x + 1 = 5
JA
A - B = 5
Niin:
x+1 = a - b
4.- Peruutusominaisuus
Tasa -arvoa ei muuteta, jos molemmissa jäsenissä on sama määrä, joka lisää (tai vähentää) ja päätetään poistaa tämä tai peruuttaa tämä. Tämä on summan peruutusominaisuus.
Otetaan esimerkki seuraava numeerinen tasa -arvo, jossa 10 esiintyy sekä oikean ja vasemman jäsenen jäsenessä:
Se voi palvella sinua: trigonometriset toiminnot: Basic, Cartesian tasossa, esimerkkejä, liikunta2 + 2 + 10 = 6 - 2 + 10
Numero 10 voidaan peruuttaa tasa -arvon menettämättä pätevyyttään, jättäen toisen lyhyemmän tasa -arvon ja vastaavat edellistä:
2 + 2 = 6 - 2
Tasa -arvossa (10 ÷ 2) - 3 = 5 - 3 Kokonaisluku - 3 kuuluu molemmille tasa -arvon jäsenille ja näkyy lisäävänä, siksi voidaan peruuttaa, hankkimalla:
10 ÷ 2 = 5
Sitä tapahtuu myös kirjaimellisilla määrillä, esimerkiksi:
Kyllä x + 2y + z = −a + b + z
Sitten "z" voidaan peruuttaa, koska se löytyy tasa -arvon molemmilta puolilta lisäämisen (ja samalla merkinnällä).
Näin tehdessään se tulokset:
x + 2y = −a + b
Se voi myös määritellä kertolaskujen peruutusominaisuuden. Jos sama määrä c kertoo molemmat tasa -arvon jäsenet, tämä määrä voidaan peruuttaa, esimerkiksi:
Cx = cy
Sitten C voidaan peruuttaa saadaksesi yksinkertaisesti:
x = y
5.- Yhtenäisyysominaisuus
Tasa -arvo pysyy muuttumattomina lisäämällä, vähentämällä, kertomalla tai jakamalla samalla määrällä saman määrän.
Esimerkiksi sen on 8 + 5 = 13, jos molemmat jäsenet moninkertaistuvat tietyllä mielivaltaisella luvulla c = 2, tasa -arvo on:
(8+5) × 2 = 13 × 2
13 × 2 = 26
Matemaattiset tasa -arvoiset luokat
Matemaattisia tasa -arvoja on erityyppisiä, joten ne luokitellaan parhaan ymmärryksensä suhteen:
-Identiteetti, Ne ovat tasa -arvoa, jossa molemmat jäsenet ovat identtisiä:
2 = 2
x = x
2x = x + x
ja niin edelleen.
-Yhtälöt, Nämä ovat yhtäläisyyksiä, joissa yksi tai useampi tuntematon esiintyminen esiintyy ja ovat totta tietyille arvoille, ts. Tasa -arvoa ei saavuteta millään mielivaltaisella arvolla, joten ne tunnetaan myös nimellä ehdolliset yhtäläisyydet. Esimerkkejä:
x + 1 = 5
x3 = 27
A + B = 40
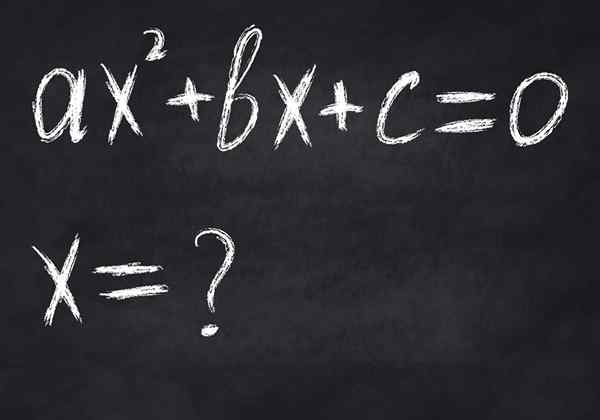 Kuva 2.- Yhtälö on ehdollinen matemaattinen tasa -arvo, koska se täyttyy vain tietyille muuttuja -arvoille. Kuva näyttää toisen asteen yhtälön, jolla on korkeintaan kaksi todellista ratkaisua
Kuva 2.- Yhtälö on ehdollinen matemaattinen tasa -arvo, koska se täyttyy vain tietyille muuttuja -arvoille. Kuva näyttää toisen asteen yhtälön, jolla on korkeintaan kaksi todellista ratkaisua -Ekvivalenssit, Heissä vasemman jäsen vastaa oikealla olevaa, vaikka ne eivät olisikaan yhtä suuret, esimerkiksi: 23 = 8.
Voi palvella sinua: Lisäaineperiaate-Kaavat, Se on tasa -arvo, joka on aina toteutettu riippumattoman muuttujan arvoille, kuten etäisyyden D hyvin tunnetussa kaavassa riippuen liikkuvan liikkuvuuden ajasta t, jolla on tasainen suorasuntelo: D = v ∙ t
Ratkaisut
Harjoitus 1
Kirjoita numero 10 - neljä erilaista ja vastaava tasa -arvo.
Ratkaisu
Kaikki nämä tasa -arvon ilmaisunumero 10, mutta eri tavoin:
5 × 2 = 10
11-1 = 10
101= 10
20 ÷ 2 = 10
Harjoitus 2
Mikä on x: n arvo, joka täyttää tasa -arvon x + 1 = 3?
Ratkaisu
Tämä tasa -arvo on yhtälö, koska x: n arvoa ei tunneta. Ominaisuuden 5 käyttämällä, jos lauseke x + 1 = 3 lisätään (−1) symbolin "=" molemmin puolin, tasa -arvo on:
x + 1 + (−1) = 3 + ( - 1)
Kun lisäät (−1) vasemman jäsenen ja operaation ratkaisu, "X" on yksin tasa -arvon vasemmalla puolella, tätä menettelyä kutsutaan puhdistus-
x + 1 - 1 = 3−1
x = 2
Siksi arvo, joka tyydyttää tämän tasa -arvon, on x = 2.
Harjoitus 3
Jos yhtenäisellä suorakulmiolla olevalla liikkuvalla liikkuvalla nopeudella on 2.5 m/s, mikä on etäisyys 3 sekunnin kuluttua?
Ratkaisu
Edellisessä osassa havaittua kaavaa käytetään, D = v ∙ t, jossa V: n arvo korvataan:
D = 2.5 ∙ t
Lausekeesta tulee tasa -arvo, kun t = 3 sekuntia ja operaatio ratkaistaan:
D = 2.5 ∙ 3 m = 7.5m
Mikä johtaa tasa -arvoon:
D = 7.5m
Viitteet
- Barnett, r. 2000. Esikytkestys. Neljäs. Painos. McGraw Hill.
- Larson, r. 2012. Esikytkestys. Kahdeksas. Painos. Cengage -oppiminen.
- Pérez, V. Algebrallisen tasa -arvon ominaisuudet. Toipunut: matematiikka.Laguia2000.com.
- Tasa -arvon ominaisuudet. Haettu: PPS.K12.Tai.meille.
- Stewart, J. 2007. Pre-laskenta: Laskentamatematiikka. Viides. Painos. Cengage -oppiminen.

