Homologiset puolet

Selitämme, mitkä homologiset puolet ovat, esimerkkejä ja harjoituksia on ratkaistu

Mitkä ovat homologiset puolet?

Se homologiset puolet Kahdessa litteässä geometrisessa luvussa ovat ne, jotka vastaavat toisiaan, pitäen samankaltaisuuden. Esimerkiksi henkilön oikea käsi on homologinen toisen henkilön oikean käden kanssa.

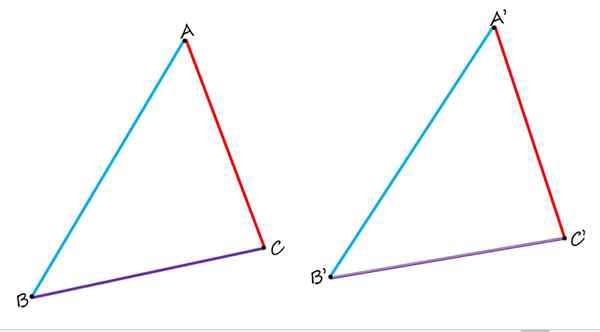
Litteässä geometriassa ei ole vain homologisia puolia, vaan myös kärkipisteitä ja homologisia kulmia. Tarkastele sitä seuraavaa lukua, joka koostuu kahdesta identtisestä kolmiosta ABC ja A'b'c ':

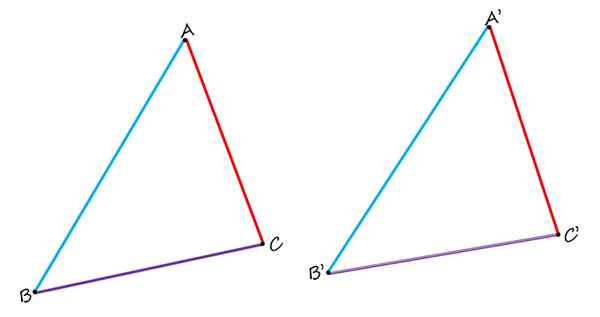Kahdessa esitetyssä kolmiossa, AB ja A'b "ovat homologisia, samoin kuin puolet BC ja B'c 'ja AC ja A'c'. Lähde: f. Zapata.

Vertaamalla niitä on selvästi havaittu, että sivut ab ja a'b 'ovat homologisia, koska ne miehittävät samanlaisen aseman jokaisessa kolmiossa. Sivut bc ja b'c 'violetissa ovat myös homologisia. Ja lopuksi, punainen vaihtovirta on homologinen sivulle A'C '.

Selitys

Edellä mainitulta seuraa, että homologiset puolet ovat ne, jotka käyttävät samaa suhteellista sijaintia kuvioissa samalla tavalla. Edellisessä kuvassa idean näyttämiseen käytettiin kahta identtistä kolmiota, mutta tämä voi helposti yleistää muita litteitä geometrisia hahmoja, jotka muodostuvat peräkkäisillä puolilla, jotka sulkevat.

Näitä lukuja kutsutaan monikulmio. Esimerkiksi kolmiot ja kvadrilateriaalit ovat vastaavasti 3 ja 4 sivua.

Homologisten puolten käsite on tärkeä, koska se mahdollistaa monikulmioiden samankaltaisuuden kriteerit, kuten pian nähdään. Samankaltaisilla kuvioilla on täsmälleen sama muoto ja ne pitävät identtisen osuuden sivujensa välillä, vaikka ne eivät olisi samankokoisia.

Ja vaikka toistaiseksi viittasi vain tasaisiin lukuihin, on myös samanlaisia ​​lukuja kolmessa ulottuvuudessa. Niitä havaitaan helposti supermarketin hyllyillä, kun sama tuote myydään identtisissä astioissa, mutta eri kokoisina.

Voi palvella sinua: matemaattinen logiikka

Muut sanat, joita käytetään vaihtavasti geometriassa viittaamaan homologisiin puoliin geometrisissa hahmoissa, ovat: vastaavat sivut, vastaavat sivut ja vastaavat sivut.

Homologiset kärkipisteet ja kulmat

Kuten sivut, myös määritellään homologiset kärkipisteet, jotka yhdistävät homologisten puolten paria. Esimerkiksi kärjet a ja 'edellisestä hahmosta ovat homologisia. Samoin kärkipaikat B ja B 'ja C ja C' ovat homologisia.

Lopuksi homologiset kulmat käyttävät samaa suhteellista sijaintia kuvioissa. Homologisten kulmien kärkipisteet ovat puolestaan ​​homologisia.

Idean havainnollistamiseksi vasemman kolmion sinisten ja purppuraiden sivujen välinen kulma, joka voidaan merkitä nimellä ∠ABC. Tämän kulman vastine on kulmassa ∠A'B'C 'kolmiosta oikealle.

Tämän kulman kärki on B, joka, kuten aiemmin on osoitettu, on vastine, jossa on B ', ja esitetyt kolmioiden kaksi paria homologisia kulmia ovat:

• ∠BCA ja ∠B'C'A '
• ∠CAB ja ∠C'A'B '

Polygonien samankaltaisuus

Jotta kaksi kahta monikulmio on samanlainen, seuraavat olosuhteet on täytettävä:

• Kaikilla homologisten kulmien parilla on sama mitta
• Hänen homologisten sivujen parit ovat verrannollisia.

Nämä kaksi ehtoa on täytettävä samanaikaisesti samankaltaisuuden varmistamiseksi. Heti havaitaan miksi.

Seuraavassa kuvassa on kaksi kvadrilateriaalia, jotka eivät selvästikään ole samanlaisia. Se johtuu siitä, että viikoittain ensimmäinen tila toteutuu, mutta toinen ei:

Kaksi kvadrilateriaalia, jotka eivät ole samanlaisia, vaikka niiden homologiset näkökulmat ovat yhtä suuret. Lähde: f. Zapata.

Vaikka kuvioissa heidän homologisten kulmien parilla on sama mitta, koska kaikki ovat suorakulmia (ne mittaavat 90º), luvut eivät ole samanlaisia, koska niiden sivuparit eivät ole verrannollisia.

Voi palvella sinua: injektiotoiminto: mistä se koostuu, mihin se on ja esimerkkejä

Toisaalta näillä kahdella nelikulmaisella on homologiset puolet yhtä suurella tasolla, mutta homologiset kulmat eivät mittaa samaa. Siksi luvut eivät selvästikään ole samanlaisia.

Kaksi neljännestervettä, joilla on saman mittauksen homologiset puolet, mutta erilaisilla sisäkulmilla, siksi ne eivät ole samanlaisia ​​lukuja. Lähde: f. Zapata.

Samankaltaisuus

Jos kaksi lukua on samanlainen, homologisten puolten välinen osuus on sama ja sitä kutsutaan samankaltaisuus.

Merkitsee yhden hahmon sivujen, kuten A, B, C, D ... ja toisen luvun vastaavat sivut, kuten A ', B', C ', D

Samanlaisten lukujen kehät ja alueet

Samankaltaisuussuhde mahdollistaa suhteiden saamisen kahden samanlaisen luvun kehän, alueiden ja määrien välillä.

Kehä syy kahdelle vastaavalle lukulle

Polygonin kehä P määritetään kaikkien sivujen summana. Jos sinulla on luku, jonka sivut ovat ', b', c ', d' ..., sen kehä P 'on:

P '= a' + b ' + c' + d '.. .

Jos toinen monikulmio on samanlainen kuin tämä, ja sen sivut ovat A, B, C, D ..., se täyttyy:

Ja siksi:

A = r ∙ a '

Voit vahvistaa saman tämän luvun toiset puolet. Joten kehä P ilmaistaan ​​seuraavasti:

P = a + b + c + d .. . = r ∙ a ' + r ∙ b' + r ∙ c ' + r ∙ d' +…

Koska "R" on yleinen tekijä kaikille addiktioille, P: n ja P: n välinen suhde on:

P = r ∙ p '

Tämä tarkoittaa, että syy kahden samankaltaisen monikulmion välisten kehien kanssa on yhtä suuri kuin samankaltaisuuden syy.

Syy kahden samanlaisen luvun alueille

Jos kahdessa samanlaisessa luvussa on alueet A ja A ', nämä liittyvät:

Voi palvella sinua: Formula -selvitysharjoitukset

A = r²∙ A '

Missä "r" on syy lukujen samankaltaisuuteen.

Kahden samanlaisen luvun tilavuussuhde

Ne ovat kaksi samanlaista kolmen dimensionaalista lukua, joiden tilavuudet ovat vastaavasti v ja v '. Heidän välinen suhde "R": n kautta on:

V = r³∙ V '

Esimerkit

Piirustukset

Osa maasta, rakennuksen kasvi tai jopa vaatekappale, pienemmässä mittakaavassa paperiarkilla voidaan edustaa. Suunnitelmien etuna on, että pystyt ottamaan mukanaan ja tekemään asiaankuuluvat muutokset helposti, ennen kuin otetaan käyttöön oikeassa esineessä.

Kartat

Ne ovat yleensä esityksiä suuren maa -alueen tasolla kylästä mantereille. Ne tehdään myös tietyssä mittakaavassa.

Heillä on lukuisia sovelluksia ja tyyppejä on monia. Esimerkiksi kartan kautta maasto voidaan kuvata, ja kun se sijaitsee tietyllä pisteellä, paras reitti siitä kohdasta toiseen määritetään.

Malli

Ne ovat kolmiulotteisia esityksiä esineiden, kuten autojen, rakennusten ja rakenteiden, mittakaavassa.

Liikuntaa

Seuraavat arvot vastaavat parin samanlaisen kolmion sivuja. Löydä syy "x": n ja "y": n samankaltaisuuteen ja arvoihin:

Kolmio 1: 5, 8, 10

Kolmio 2: 150, x, y

Ratkaisu

Syy samankaltaisuuteen on osamäärä:

R = 150/5 = 30

Siksi:

x = 30 × 8 = 240

y = 10 × 30 = 300