Darcy -laki

Selitämme, mikä on Darcyn laki, sen yhtälöt, hakemukset, rajoitukset ja ehdotetaan ratkaistava harjoitus

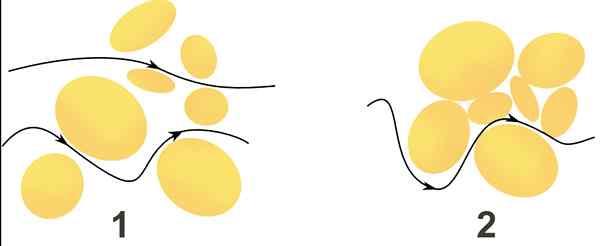
Vesivirta kahden huokoisen väliaineen läpi on merkitty mustien nuolien kautta. Keskipitkällä 1 virtaus liikkuu nopeammin kuin keskellä 2, koska nopeus riippuu välien koosta ja niiden välisestä viestinnän helppoudesta. Lähde: Wikimedia Commons.

Mikä on Darcyn laki?

Se Darcy -laki Se on matemaattinen suhde, jota sovelletaan nesteiden virtaukseen läpäisevässä tai huokoisessa väliaineessa, esimerkiksi vesi, joka valuu hiekkaan.

Nesteen edetessä huokoisen läpi, sen hydrostaattinen paine vaihtelee, erityisesti se on suurempi lähdettä lähinnä olevissa pisteissä ja alhaisempi viemäröintia lähinnä olevissa kohdissa. Tällä tavoin hydraulisen gradientin käsite ilmestyy, fyysinen määrä, joka merkitään kirjaimella I.

Toisaalta huokoinen väliaine on ominaista määrä nimeltään Hydraulinen johtavuus K -k -. Huokoisuuden välillä on selvästi suhde, jonka määritetään K, hydraulinen gradientti I ja poikkileikkauksen Q Q yksikköä kohti.

Heidän välinen suhde löysi ranskalainen hydraulinsinööri Henry Darcy (1803-1858), joka vastasi kotikaupunginsa vesihuoltoa: Dijon.

Darcyn laki esitettiin vuonna 1856 perusteellisessa työssä, jossa lakiin liittyvät fyysiset määrät ovat yksityiskohtaisia, suoritetut kokeet ja erityisesti nimeltään laite kevante.

Darcy Law -yhtälöt

Darcyn laki osoittaa useiden fyysisten määrien välisen suhteen, jotka kuvaavat virtausta huokoisen väliaineen läpi. Se osoittaa, että veden virtaus Q - joka liikkuu tietyn huokoisen keinon läpi, on suoraan verrannollinen poikkileikkaukseen, joka on lävistetty ja hydraulinen gradientti Yllyttää-

Q ∝ a ∙ i

Voi palvella sinua: Yhtenäinen suorakulmainen liike: Ominaisuudet, kaavat, harjoitukset

Suhteellisuusvakio on huokoisen ympäristön läpäisevyys K, jota kutsutaan myös Hydraulinen johtavuus. Tällä tavalla Darcyn laki esitetään seuraavasti:

Q = k ∙ a ∙ i

Darcyn lain erilainen muoto

Darcyn yhtälö voidaan ilmaista erotussuhteena virtausnopeuden välillä jokaisessa pisteessä ja paikallisen hydraulisen gradientin välillä:

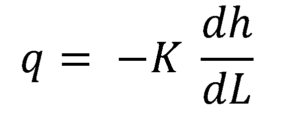
Koska hydraulinen gradientti on negatiivinen määrä, kun se lasketaan virtauksen suuntaan, on sitten tarpeen moninkertaistaa hydraulisen johtavuuden negatiivilla keskimääräisen virtausnopeuden q saamiseksi, kussakin poikkileikkauksessa.

Sitten Darcyn laissa olevat suuruudet analysoidaan yksityiskohtaisemmin.

Virtaus, hydraulinen kaltevuus ja läpäisevyys

1.- Flow q

Virtaus määritellään veden tilavuutena, joka kiertää tietyn poikkileikkauksen läpi virtauksen suuntaan, aikayksikköä kohti:

Q = Δv / ΔT

SI -yksiköiden kansainvälisessä järjestelmässä virtaus mitataan kuutiometreinä sekunnissa, mutta se ilmaistaan ​​usein litrana minuutissa tai litraa sekunnissa.

Q -pinta -alayksikköä kohti vaaditaan usein, mikä on Q -virtauksen ja poikkileikkauksen välinen suhde:

q = q / a

SI: ssä q ilmaistaan ​​m/s, minkä vuoksi Q edustaa nesteen keskimääräistä nopeutta putken poikkileikkauksessa.

On tärkeää huomata, että vaikka virtaus Q on sama putken kaikissa osissa, pinta -alayksikköä kohden tai yksinkertaisesti virtausnopeus on suurempi kapeimmissa ja pienemmissä osissa laajemmassa.

2.- Hydraulinen kaltevuus I

Kun neste kiertää huokoista väliainetta, hydrostaattinen paine laskee samaan virtauksen suuntaan.

Voi palvella sinua: Ton: Muutokset, vastaavuudet ja harjoitukset ratkaistu

On tiedossa, että hydrostaattinen paine, tietyssä putken kohdassa, on verrannollinen korkeuteen H, joka merkitsee avoimen putken painemittarin siinä paikassa. Suhteellisuusvakio on nesteen tiheyden tuote, joka johtuu painovoiman kiihtyvyydestä.

Tällä tavoin hydraulinen gradientti I määritellään kahden manometrin ja ΔL: n pylväiden korkeuseron ΔH välisellä suhteella. Jälkimmäinen on etäisyys, joka erottaa manometrit (katso alla oleva kuva):

I = ΔH / ΔL

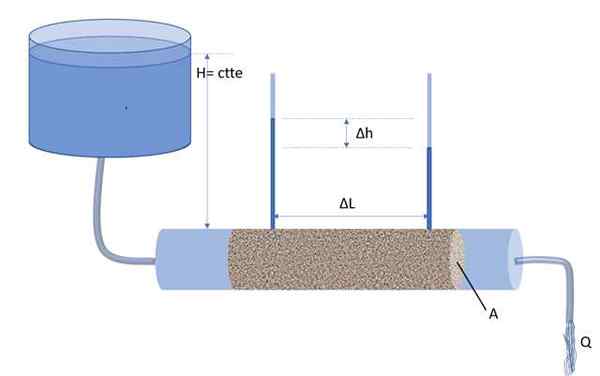Permemememittari, Henry Darcyn keksimä laite kvantifioimaan veden virtaus huokoisen väliaineen läpi. Lähde: f. Zapata.

Tämä on keskimääräinen hydraulinen gradientti pitkän ΔL: n osassa, mitoiton määrä ja myös negatiivinen.

Jos haluat löytää hydraulisen gradientin jokaisesta putken kohdasta, rajan otetaan ΔL: n taipumus nollaan, mikä johtaa hydraulisen gradienttifunktion johdannaiseen asentoon L, virtausta pitkin:

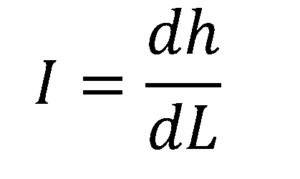
3.- Läpäisevyys k

Huokoisen keinon läpäisevyys tai hydraulinen johtavuus on virtauksen välinen suhde Q - ja poikkileikkauksen tuote -Lla Hydraulinen kaltevuus Yllyttää-

K = q / a ∙ i

Hydraulisella johtavuudella on nopeusyksiköt, mittarit itsessään.

K: n yksikkö on määritelty, nimeltään Darcy, Henry Darcyn kunniaksi ja määritelty seuraavasti:

Eräs Darcy Se on nesteen millilitran läpäisevyys, jossa on sentboisen viskositeetti, joka liikkuu senttimetriä ilmakehän differentiaalisessa paineessa, neliön senttimetrin poikkileikkauksen kautta.

Darcy Law -hakemukset

Darcyn lain pääkäyttö on ennustaa veden virtausta pohjakerroksen varrella, ennen kaivojen poraamista.

Voi palvella sinua: Dimensional Analysis

Myös Darcyn lakia käytetään säännöllisesti maatalouden ja hydrologisessa tekniikassa. Sitä voidaan käyttää myös öljyteollisuudessa kuvaamaan kaasun ja öljyn virtausta huokoisissa väliaineissa. Tällöin K voi kuitenkin vaihdella kaasun tai öljyn virtauksesta riippuen, eikä se voi riippua yksinomaan ja yksinomaan läpäisevästä substraatista.

Rajoitukset

Darcyn laki olettaa, että hydraulinen johtavuus K on määrä väliainetta, mikä on totta monissa tapauksissa. Joskus K riippuu kuitenkin nesteen dynaamisesta viskositeetista, mikä puolestaan ​​voi riippua virtausnopeudesta ja lämpötilagradienteista.

Darcyn oletus on uskottavaa, kun harkitaan maanalaista vettä, jossa viskositeetti on käytännössä vakio, koska sen arvo ei melkein vaikuta muutaman lämpötilaeron perusteella.

Öljynvirtaustapauksissa huokoisten keinojen kautta Darcy -yhtälöä ei voida soveltaa tässä esitetyllä tavalla, mutta tietyt muutokset sisällytetään, jotka ylittävät tämän artikkelin tarkoituksen.

Liikuntaa

Määritä rannan hiekan hydraulinen johtavuus käyttämällä laboratoriotapaa.

Oletetaan, että kevanemerkkiputken halkaisija on 20 cm ja että kahden manometrin välinen etäisyys on 50 cm. On myös tiedossa, että vesi virtaa nopeudella 300 kuutiometriä desimetriä minuutissa ja kahden manometrin välinen tasoero on 25 cm.

Ratkaisu

Virtaus, joka on 300 kuutiometriä desimetriä minuutissa, mutta joka ilmaisee kansainvälisen järjestelmän yksiköissä, se olisi näin:

Q = 300 x 10^-3 m³ / 60 s = 5 x 10^-3 m³ / s

Poikkileikkaus A lasketaan:

A = π ∙ r² = π ∙ (10 cm)² = π ∙ (0,1 m)² = 0,314 m²

Hydraulinen gradientti I on osoitus manometrisen korkeuseron ja manometrien erottamisen välillä:

I = 25 cm / 50 cm = 0,5

Edellä annettujen hydraulisen johtavuuden määritelmän mukaan:

K = q / a ∙ i = (5 x 10^-3 m³ / s) / (0,314 m² ∙ 0,5) = 3,185 x 10^-2 m/s ≈ 2 m/min.