Lenzin kaavalaki, yhtälöt, sovellukset, esimerkit

Se Lenzin laki Se osoittaa, että indusoidun elektromotorisen voiman napaisuus suljetussa piirissä johtuen magneettikentän virtauksen vaihtelusta johtuen sellaisesta, että se vastustaa mainitun virtauksen variaatiota.

Faradayn lakiin asetettu kielteinen merkki ottaa huomioon Lenzin lain, joka on syy siihen, miksi sitä kutsutaan Faraday-Lenz-laki ja joka ilmaistaan ​​seuraavasti:

Kuvio 1. Toroidinen kela pystyy indusoimaan virtoja muissa kuljettajissa. Lähde: Pixabay.

[TOC]

Kaavat ja yhtälöt

ε edustaa indusoitua sähkömoottorin voimaa, lyhennettynä Fem, Φ Se on magneettikenttävirta ja t On aika. Yksiköt kansainvälisessä järjestelmässä (SI) Fem Ne ovat voltteja (v).

Puolestaan ​​magneettikentän virtaus Φ Se on määritelty seuraava skalaarituote:

Niin paljon B - kuten n Ne ovat vektorialueita ja niitä voidaan merkitä lihavoitulla tai nuolella kirjaimella. B - Se on magneettikentän vektori ja n Se on yksikkövektori (suuruusluokka 1) kohtisuorassa pintaan, jonka ylittää B -.

Esitetyssä yhtälössä B - Se on vakio ja yksikkö Φ Magneettikentän virtauksen SI on Weber (W):

1 weber = 1 Tesla. metri²

Toinen tapa ilmaista Φ Se on saatu käyttämällä skalaarituotteen määritelmää:

Φ = b.-Lla.cos θ

Tässä yhtälössä, B - Se on magneettikentän suuruus (ilman rohkeaa tai nuolta, erottaa vektori sen suuruudesta), A on kentän ylittämän pinnan pinta -ala ja θ on vektorien välinen kulma B - ja n.

Magneettikentän virtausta voidaan muuttaa eri tavoin ajan myötä, jotta voidaan luoda a Fem indusoitu silmukassa - suljetussa piirissä - alueella. Esimerkiksi:

-Magneettikentän muuttujan tekeminen ajan myötä: B - = B - (T), Alueen ja vakiokulman pitäminen sitten:

-Spaase -alue voi vaihdella, antaen muiden suuruuksien vakiona:

 -Kulma B - Ja pintaa vaihdetaan spaasin pyörimisellä, tällä tavalla saadaan sinimuotoinen generaattori:

Parempi vielä, jos yhden silmukan sijasta käytetään nougasia, siinä tapauksessa Fem Kerro n kertaa:

 Tietenkin magneettikentän virtaus voidaan muuttaa millä tahansa näiden muotojen yhdistelmällä, vaikka se olisi jonkin verran monimutkaisempaa kuvata.

Sovellukset

Lenzin lain välitön soveltaminen on määrittää Fem tai indusoitu virta ilman tarvetta suorittaa laskelmia. Mieti seuraavaa: Sinulla on silmukka magneettikentän keskellä, kuten se, joka tuottaa palkkimagneetin.

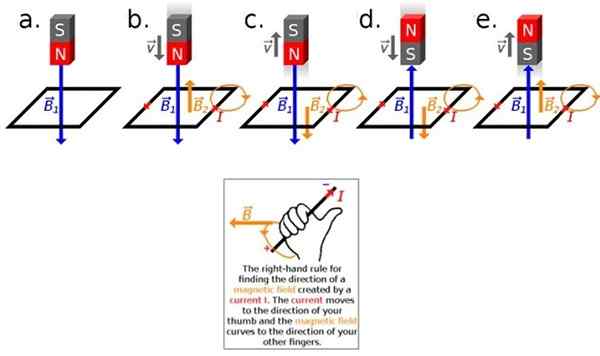Kuva 2. Lenzin lain soveltaminen. Lähde: Wikimedia Commons.

Jos magneetti ja silmukka ovat levossa toisessa suhteessa toisiinsa, eli ei ole indusoidut virtaa, koska magneettikentän virtaus pysyy vakiona siinä tapauksessa (katso kuva 2a). Virran indusoimiseksi on välttämätöntä, että virtaus vaihtelee.

Nyt, jos magneetin ja spaasin välillä on suhteellinen liike joko siirtämällä magneettia kohti spaasia tai on kohti magneettia, mitataan virtaa (kuva 2b eteenpäin).

Tämä indusoitu virta puolestaan ​​tuottaa magneettikentän, siksi meillä on kaksi kenttää: magneetti B -₁ sinisellä ja induktion luomaan virtaan liittyvään virtaan B -₂, oranssina.

Oikean peukalon hallitsija antaa sinun tietää suunnan B -₂, Tätä varten oikean käden peukalo asetetaan virran suuntaan ja suuntaan. Muut neljä sormea ​​osoittavat suunnan, johon magneettikenttä on kaareva, kuvan 2 mukaan (alla).

Voi palvella sinua: Conpex Mirror

Magneetin liikkuminen spaasin läpi

Sanotaan. Magneetin kenttäviivat poistuvat pohjoisnavasta n ja tulevat eteläiseen napaan. Joten φ, luomalla virtauksella tapahtuu muutoksia B -₁ Se ylittää silmukan:Φ kasvaa!  Siksi silmukassa luodaan magneettikenttä B -₂ Vastakkaisella tarkoituksella.

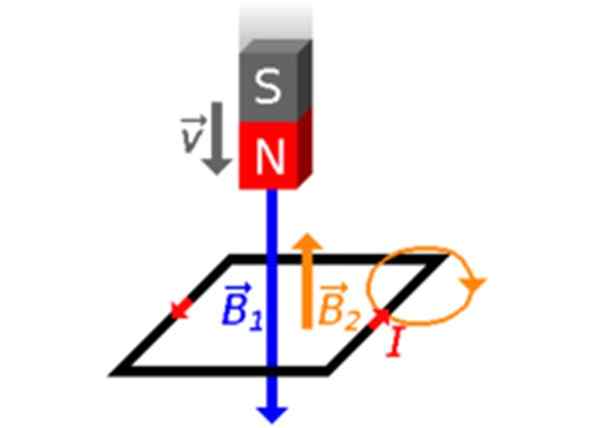Kuva 3. Magneetti liikkuu kohti silmukkaa hänen pohjoisnavan kanssa hänelle. Lähde: Wikimedia Commons.

Indusoitu virta on järkevää ristiriidassa kellon neulojen kanssa, -FLECHAS PUNAINEN kuvioissa 2 ja 3-, oikean peukalon säännön mukaan.

Siirrätään pois Spiran magneetti ja sitten hänen Φ vähenee (kuviot 2C ja 4), joten silmukka on nopea luoda magneettikentän sisälle B -₂ Samoin kompensoida. Siksi indusoitu virta on aika, kuten voidaan nähdä kuvasta 4.

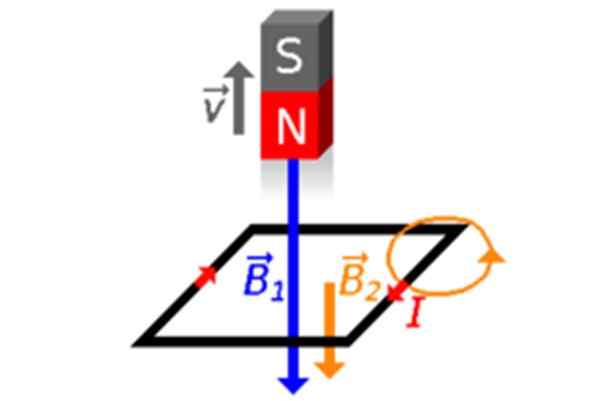Kuva 4. Magneetti siirtyy pois silmukasta, aina hänen pohjoisnavan kanssa osoittaen hänelle. Lähde: Wikimedia Commons.

Sijoittaa magneetin sijainti

Mitä tapahtuu, jos magneettipaikka sijoitetaan? Jos etelänapa osoittaa silmukkaan, kenttä osoittaa, koska linjat B - Magneetissa he poistuvat pohjoisnavasta ja tulevat etelänavalla (katso kuva 2d).

Heti Lenzin laki ilmoittaa, että tämä pystysuuntainen kenttä ylöspäin, joka saostaa silmukkaa, aiheuttaa tässä vastakkaisen kentän, toisin sanoen, B -₂ alas ja indusoitu virta on myös aika.

Lopulta hän siirtää La Espiran magneetin, aina etelänavan ollessa osoittaen tämän sisälle. Sitten silmukan sisällä on kenttä B -₂ Osallistua magneetin poistoon, joka ei muuta kenttävirtaa siinä. Niin paljon B -₁ kuten B -₂ Heillä on sama merkitys (katso kuva 2d).

Lukija ymmärtää, että kuten lupasimme, ei ole tehty laskelmia indusoidun virran suunnan tuntemiseksi.

Kokeet

Heinrich Lenz (1804-1865) suoritti lukuisia kokeellisia teoksia koko tieteellisen uransa ajan. Tunnetuimpia ovat juuri kuvaamiamme, omistautuen mittaamaan voimia ja magneettisia vaikutuksia, jotka on luotu pudottamalla äkillisesti magneetti silmukan keskelle. Tuloksillaan hän hienosti Michael Faradayn tekemää työtä.

Tämä negatiivinen merkki Faradayn laissa osoittautuu kokeeksi, jolle se on tänään tunnustettu. Lenz teki kuitenkin monia töitä geofysiikassa nuoruutensa aikana ja sillä välin hän oli omistautunut pudottamaan magneetteja käännösten ja putkien sisälle. Hän tutki myös sähkövastusta ja metallin johtavuutta.

Erityisesti lämpötilan nousun vaikutukset vastusarvoon. Hän tarkkaili jatkuvasti, että langan lämmittäessä vastus vähenee ja häviää lämpöä, jota James Joule myös havaitsi itsenäisesti.

Muistaa ikuisesti heidän panoksensa sähkömagneettisuuteen hänen nimensä kantaavan lain (kelaihin) lisäksi ne on merkitty L -kirjaimella L -kirjaimella.

Voi palvella sinua: Thévenin -lause: mitä koostuu, sovellukset ja esimerkit

Lenzin putki

Se on koe, jossa se osoitetaan magneettina, kun se vapautuu kuparin putken sisällä. Magneetti putoamisen aikana tuottaa muunnelmia magneettikentän virtauksessa putken sisällä, samoin kuin voimankierrossa.

Sitten syntyy indusoitu virta, joka vastustaa virtauksen muutosta. Putki luo tämän oman magneettikentän, joka, kuten me jo tiedämme, liittyy indusoituun virtaan. Oletetaan.

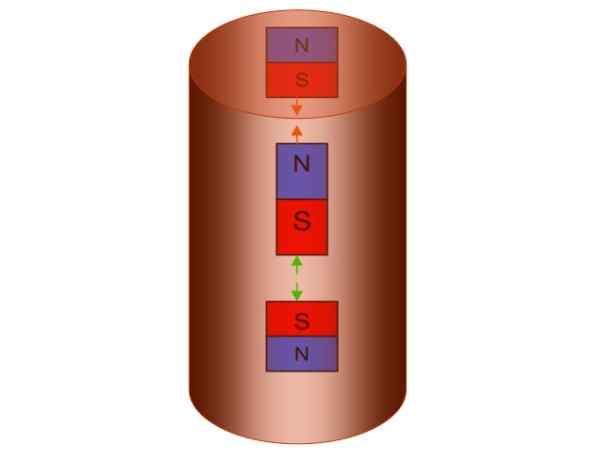Kuva 5. Lenzin putki. Lähde: f. Zapata.

Seurauksena on, että putki luo oman magneettikentänsä pohjoisnavalla alas ja etelänapa ylöspäin, mikä vastaa parin kuvitteellisen magneetin luomista, yksi yläpuolella olevasta ja toisesta, joka putoaa.

Konsepti sisältyy seuraavaan kuvaan, mutta on tarpeen muistaa, että magneettiset navat ovat erottamattomia. Jos alemmassa kuvitteellisessa magneetissa on pohjoisnapa alas, se seuraa välttämättä etelää ylöspäin.

Kun vastakkaiset puolalaiset houkuttelevat ja vastakohdat torjuvat, putoamisen magneetin hylätään ja samalla ylempi kuvitteellinen magneetti houkuttelee sitä.

Nettovaikutus on aina jarrutus, vaikka magneetti vapautuu pohjoisnavan ollessa alaspäin.

Joule-Lenzin laki

Joule-Lenzin laki kuvaa osana energiaa, joka liittyy kuljettajan kiertämään sähkövirtaan, menetetään lämmön muodossa. Vaikutus, jota käytetään sähkölämmittimissä, levyissä, hiustenkuivaajissa ja sähkö liesissä, muun muassa laitteissa.

Kaikilla heillä on vastus-, filamentti tai lämmityselementti, joka kuumenee virran kulkemiseen.

Matemaattisessa muodossa, olipa se sitten R - Lämmityselementin vastus, Yllyttää sen läpi kiertävä nykyinen voimakkuus ja t Aika, Joule Effect -tuotannon määrän lämpö on:

Q = i². R -. t

Missä Q - Se mitataan Joulesissa (SI -yksiköt). James Joule ja Heinrich Lenz löysivät tämän vaikutuksen samanaikaisesti noin vuonna 1842.

Esimerkit

Seuraavassa esitetään kolme tärkeää esimerkkiä, joissa Faraday-Lenzin lakia sovelletaan:

Vaihtovertainen generaattori

Vaihtovirtageneraattori muuttaa mekaanisen energian sähköenergiaksi. Perusta on kuvattu alussa: silmukka kierretään tasaisen magneettikentän keskellä, kuten se, joka on luotu suuren sähkömagneetin kahden navan väliin. Kun sitä käytetään N spiraalit, Fem kasvaa suhteessa N.

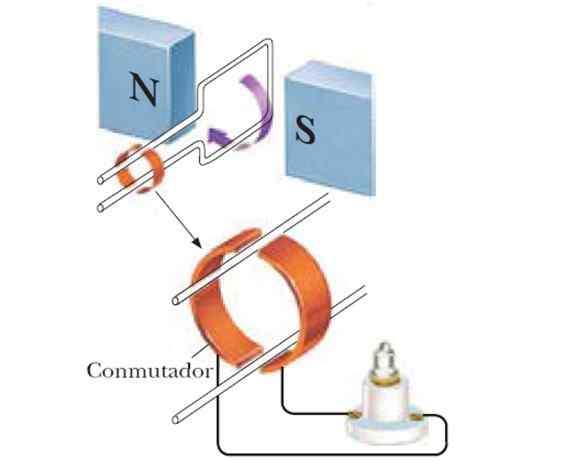Kuva 6. Vuorotteleva virtageneraattori.

Kun silmukka käännetään, normaali vektori pintaan muuttaa sen suuntausta kentän suhteen, mikä tuottaa a Fem joka vaihtelee sinimuotoisella tavalla ajan myötä. Oletetaan, että kiertotaajuus on Ω, Sitten vaihdettaessa alussa tapahtuneessa yhtälössä, se on:

Muuntaja

Se on laite, jonka avulla voit saada suoran jännitteen vaihtoehtoisesta jänniteestä. Muuntaja on osa lukemattomia laitteita, kuten esimerkiksi matkapuhelinlaturi.Se toimii seuraavalla tavalla:

Raudan ytimen ympärillä on kaksi kelaa, yksi kutsutaan ensisijainen ja se toinen toissijainen.  Vastaava lukumäärä on n₁ ja n₂.

Ensisijainen kela tai käämi on kytketty vaihtoehtoiseen jännitteeseen (kuten esimerkiksi kotitekoinen sähkö) lomakkeesta V_P = V₁.cos ωt, aiheuttaen vuorottelevan taajuusvirran kiertämiseen Ω.

Tämä virta on peräisin magneettikentästä, joka puolestaan ​​aiheuttaa värähtelevän magneettisen vuodon toisessa kelassa tai käämityksessä, muodon toissijaisella jännitteellä V_S = V₂.cos ωt.

Kuitenkin osoittautuu, että raudan ytimen sisällä oleva magneettikenttä on verrannollinen ensisijaisen käämityksen kierrosten lukumäärään:

Se voi palvella sinua: 13 esimerkkiä Newtonin toisesta laista jokapäiväisessä elämässä

B ∝ 1 /N₁

Ja niin se on V_P, ensisijaisen käämin jännite, kun taas Fem indusoitu V_S Toisessa käämityksessä se on verrannollinen, kuten tiedämme, käännösten lukumäärään₂ ja myös V_P.

Joten näiden suhteellisuuksien yhdistäminen on suhde V_S ja V_P joka riippuu kunkin käännösten lukumäärän välillä seuraavasti:

V_S = (N₂ /N₁) V_P

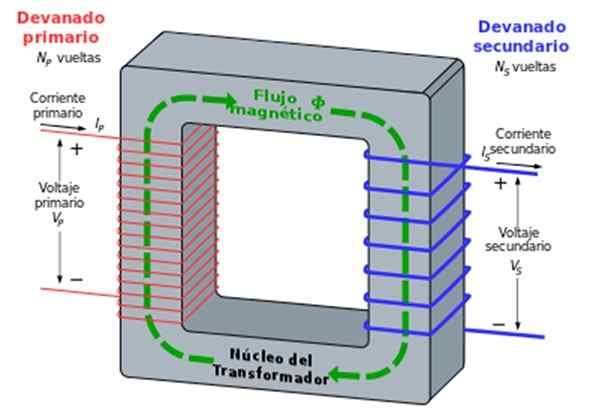Kuva 7. Muuntaja. Lähde: Wikimedia Commons. Kundalinizero [CC BY-SA 3.0 (http: // creativecommons.Org/lisenssit/by-SA/3.0/]]

Metallilekoitin

Ne ovat laitteita, joita käytetään pankeissa ja turvallisuuskentillä. Ne havaitsevat minkä tahansa metallin, ei vain raudan tai nikkelin, läsnäolon. Ne toimivat indusoitujen virtojen ansiosta kahden kelan avulla: yksi lähetin ja toinen vastaanotin.

Vaihtava korkea taajuusvirta ohitetaan lähettävässä kelassa, joten se tuottaa vaihtoehtoisen magneettikentän akselia pitkin (katso kuva), joka indusoi virran vastaanottavassa kelassa, jotain enemmän tai vähemmän samanlaisia ​​kuin muuntajan kanssa tapahtuu.

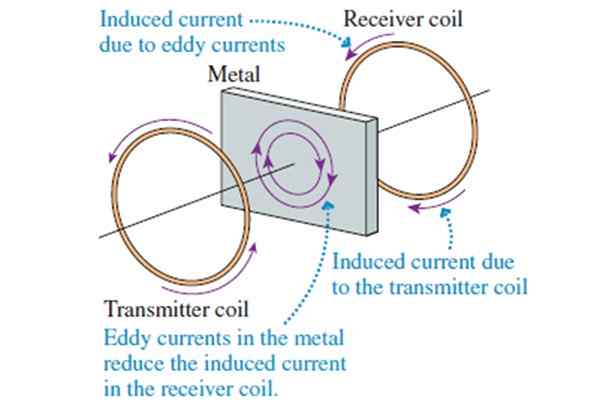Kuva 8. Metallinilmaisimen toimintaperiaate.

Jos molempien kelojen väliin asetetaan metallia, siinä ilmestyy pieniä indusoituja virtauksia, nimeltään Foucault -virrat (jotka eivät voi virtaa eristimessä). Vastaanottava kela reagoi lähettävän kelan magneettikenttiin ja Foucaultin virtojen luomiin.

Foucault -virrat yrittävät minimoida metallikappaleen magneettikentän virtaus. Siksi kenttä, joka havaitsee vastaanottavan kelan, vähenee, kun me metallikappale on molempien kelojen väliin. Kun tämä tapahtuu, hälytys, joka varoittaa metallin läsnäoloa.

Harjoitukset

Harjoitus 1

Siellä on pyöreä kela, jossa on 250 yritystä, joiden säde on 5 cm, joka sijaitsee kohtisuorassa magneettikentän kanssa 0.2 t. Määrittele Fem indusoitu, jos aikavälillä 0.1 s, magneettinen magneettikenttä kaksinkertaistuu ja osoittaa virran merkityksen seuraavan kuvan mukaan:

Kuva 9. Pyöreä spira keskellä tasaista magneettikenttää kohtisuorassa spaasitasoon nähden. Lähde: f. Zapata.

Ratkaisu

Ensin lasketaan indusoidun FEM: n suuruus, silloin liittyvän virran merkitys ilmoitetaan piirustuksen mukaan.

N = 250 käännöstä

A = π. R -² = p . (5 x 10^-2 m)² = 0.0079 m².

cos θ = cos 0 = 1 (Vektori n Se vie rinnakkain B --A

Kun magneettikenttä kaksinkertaistaa sen suuruuden, sinulla on:

Näiden arvojen korvaaminen yhtälössä Fem Indusoitu:

ε = 250. 0 -.0079 m² . 2 t/s = 3.95 V

Koska kenttä on kaksinkertaistunut, samoin on tehty magneettikentän virtaus, siksi silmukassa luodaan indusoitu virta, joka vastustaa mainittua kasvua.

Kuvan kenttä osoittaa näytölle. Indusoidun virran luoman kentän on poistuttava näytöstä soveltamalla oikeaa peukalon sääntöä, seuraa, että indusoitu virta on anti -Horary.

Harjoitus 2

Neliö käämitys koostuu 40 kierrosta 5 cm: n puolella, joka täyttää 50 Hz usein tasaisen suuruuskentän 0 keskellä.1 t. Alun perin kela on kohtisuorassa kentälle. Mikä on ilmaus Fem indusoitu?

Ratkaisu

Aikaisemmista osioista tämä ilmaus johdettiin:

ε = n.B -.-Lla. Ω. synti ωt

A = (5 x 10^-2 m)² = 0.0025 m²

N = 40 spiraalia

Ω = 2π.F = 2π.50 Hz = 100p s^-1

B = 0.1 t

ε = 40 x 0.1 x 0.0025 x 100π  X Sen 50.t =p . SEN 100π.T V

Viitteet

1. Figueroa, D. (2005). Sarja: Tieteen ja tekniikan fysiikka. Osa 6. Sähkömagnetismi. Toimittanut Douglas Figueroa (USB).
2. Hewitt, Paul. 2012. Käsitteellinen fysiikka. Viides. Ed. Pearson.
3. Ritari, r.  2017. Tutkijoiden fysiikka ja tekniikka: strategialähestymistapa. Pearson.
4. OpenX -korkeakoulu. Faradayn induktiolaki: Lenzin laki. Haettu osoitteesta: OpenTextbc.Ac.
5. Fysiikka librettexts. Lenzin laki. Toipunut: Phys.Librettexts.org.
6. Sears, f. (2009). University Physics Vol. 2.