Allekirjoittaa lakia

Selitämme merkkien lain, esimerkkejä ja harjoituksia ratkaistu

Merkkilaki

Mikä on merkkien laki?

Se Allekirjoittaa lakia Se on aritmeettisissa ja algebrallisissa laskelmissa käytettyjen sääntöjen joukko reaalilukuilla merkin oikein määrittämiseksi tulokselle, kun mukana on sekä positiivisia että negatiivisia määriä.

Suoritetun operaation mukaisesti on riittäviä sääntöjä: summa, vähennys, kertolasku ja jako, jotka ovat perusteellisimpia, ja myös potentiaatio- ja arkistointitoimenpiteisiin liittyviä merkkejä on sääntöjä.

Tietyssä operaatiossa, käsin tai laskurin kanssa, on tarpeen soveltaa merkintöjen lakia oikein oikean tuloksen varmistamiseksi, koska vain pieni muutos merkkeissä muuttaa merkittävästi määriä määriä merkittävästi.

Kunkin aritmeettisen perustoimenpiteen merkintöjen laki ja jäljempänä olevat tapaukset, joita voi esiintyä.

Allekirjoituslaki yhteensä

1) Jos lisättävillä numeroilla on sama merkki

Numerot lisätään tavalliseen tapaan ja tulos lisätään numeroiden merkkiin riippumatta siitä, onko tämä positiivinen vai negatiivinen.

On tärkeää pitää mielessä, että positiiviset numerot eivät yleensä ole ennen merkkiä, mutta ne kirjoitetaan suoraan. Toisaalta negatiiviset luvut on kirjoitettu suluihin, etenkin kun niitä edeltää aritmeettisen toiminnan symboli, sekaannuksen välttämiseksi.

Esimerkkejä numeroiden summista, joilla on sama merkki:

3 + 9 = 12
4 + 7 + 1 + 6 = 18
(−3) + (−8) = −11
(−5) + (−10) + (−6) = −21

2) Jos lisättävissä olevilla numeroilla on erilainen merkki

Numerot vähennetään ja tulokseen lisätään suurimman absoluuttinen arvo, riippumatta siitä, onko positiivinen vai negatiivinen.

Esimerkiksi suorita operaatio 5 + (−14). Koska (−14) absoluuttinen arvo on suurempi kuin 5, 5 yksikköä vähennetään 14: stä, mikä antaa 9 ja tämä tulos on asetettu negatiiviseen merkkiin:

Voi palvella sinua: prismat ja pyramidit

5 + (−14) = −9

Lisää esimerkkejä tästä säännöstä, jota sovelletaan kahden eri merkin lukumäärään, ovat:

(−27) + 12 = −15

12 + (−7) = 5

Jos operaatiossa on enemmän kuin kaksi lisäystä, joilla on erilaisia ​​merkkejä, Summan assosiatiivinen omaisuus:

(−20) + 9 + (−7) = [(−20) + 9] + (−7)

Operaatio suoritetaan ensin Pracetessa, joka koostuu kahden eri merkin lukumäärän summasta, jolle kuvattua sääntöä sovelletaan: tulos vähennetään ja numeron merkkistä, jolla on korkein absoluuttinen arvo:

(−20) + 9 = −11

Operaatio on tällainen:

(−20) + 9 + (−7) = (−11) + (−7)

Nyt sinulla on saman merkin kahden numeron summa, sitten ne lisätään yleensä ja tulos on asetettu negatiiviseksi merkki:

(−20) + 9 + (−7) = (−11) + (−7) = −18

Merkkejä korvikkeessa

Kahden numeron vähennys määritellään päinvastaiseksi. Numero on päinvastoin kuin muutettu merkki. Esimerkiksi, vastakohta 2 on (−2), vastakohta (−5) on 5 ja niin edelleen.

Tätä silmällä pitäen, kun sinulla on kaksi numeroa vähennys:

A - B

Se yksinkertaisesti muuttuu B: n vastakkaiseksi:

A + ( - b)

Ja jatka edellisessä osassa kuvatulla tavalla. Huomaa merkin + negatiivinen lukumäärä ei muuta sitä, mutta erittäin varovainen, päinvastoin ei ole totta.

Kun numero "A", joka on mutind, on suurempi kuin varastettu luku "B", kuten luonnollisten lukujen vähentämisessä. Ei hätää, koska suuri määrä vähennetään pienemmästä määrästä:

Voi palvella sinua: kolmion eriarvoisuus: esittely, esimerkit, ratkaisut harjoitukset

25 - 8 = 17

Seuraavien esimerkkien avulla menetelmä vähentää vastakkaista vähennykseen on erittäin kätevä:

(−5) - 24 = (−5) +( - 24) = - 29
32 - (−23) = 32 + 23 = 55

KIRJOITUSLAKIRJA

Käsittelymerkkejä koskevaa lakia sovelletaan tällä tavalla:

• Kertoamalla kaksi numeroa samasta merkistä, tulos on aina positiivinen.
• Kahden vastakkaisen merkkinumeron tuote on aina negatiivinen.

Yhteenveto kertolaskujen merkkisäännöstä on esitetty kuvassa:

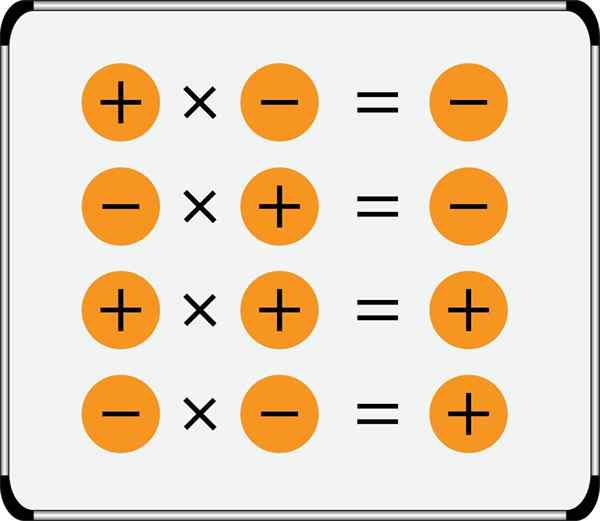
Huomaa, että positiiviset numerot voidaan kirjoittaa ilman edellistä merkkiä, mutta negatiiviset numerot ovat aina, että lisäksi kaksi aritmeettista symbolia ei koskaan kirjoiteta toisilleen, ne on aina erotettava esimerkiksi sululla:

Väärä: 3 × −4
Oikea: 3 × (−4) = −12

(−5) × 6 = −5 × 6 = −30
(−3) × (−11) = 33
10 × 27 = 270

Kerrottamiseksi enemmän kuin kaksi lukua käytetään kertolaskujen assosiatiivista ominaisuutta, koska tekijöiden järjestys ei muuta tuotetta esimerkiksi suoritettaessa:

(−2) × (−14) × 16

Voit kertoa kaksi ensimmäistä tekijää tai kaksi viimeistä, jos haluat, ja sitten kertoa tulos jäljellä olevalla tekijällä. Tässä tapauksessa nämä kaksi tekijää kerrotaan ensin vasemmalla:

[(−2) × (−14)] × 16

Kahden negatiivisen luvun tuote on positiivinen, sitten (−2) × (−14) = 28 ja pysyy:

28 × 16 = 448

Allekirjoituslaki divisioonassa

Se on analoginen kertolaskujen merkkien kanssa:

• Saman merkin kahden numeron suhde on aina positiivinen.
• Jakamalla kaksi muuten merkkinumeroa tulos on aina negatiivinen.

Se voi palvella sinua: Ero ympyrän ja kehän välillä (esimerkkien kanssa)

Esimerkiksi:

24 ÷ 8 = 3
−36 ÷ 3 = −12
162 ÷ (−9) = −18
−216 ÷ (−6) = 36

Valtuuttamisen ja arkistointien merkkien laki

Kirjallinen numero eksponentti on:

-llaⁿ

Missä "a" on pohja ja "n" on eksponentti. Kaksi tapausta erotetaan eksponentin pariteetin mukaan:

Tapaus 1: A on positiivinen

Kun pohja on positiivinen, tulos on positiivinen riippumatta siitä, onko eksponentti tasainen vai outo, kuten:

2³ = 8
3⁴ = 81

Tapaus 2: A on negatiivinen

Tässä on kaksi tapausta:

• Kun eksponentti on tasainen, tulos on positiivinen.
• Jos eksponentti on outoa, se on negatiivinen.

Esimerkit

3² = 3 ∙ 3 = 9
2³ = 2 ∙ 2 ∙ 2 = 8
(−2)⁴ = (−2) ∙ (−2) ∙ (−2) ∙ (−2) = 16
(−3)³ = (−3) ∙ (−3) ∙ (−3) = −27

Operaatiot ryhmittelysymboleilla

Ne näyttävät usein erillisistä operaatioista ryhmittelysymboleilla: sulkut, kiinnikkeet ja avaimet. Nämä poistetaan sisäpuolelta ottaen huomioon seuraavat:

• Jos ryhmittelysymbolia edeltää positiivinen merkki, se voidaan poistaa muuttamatta sisällön merkkejä, esimerkiksi: + (−3 + 5 - 1) = −3 + 5 - 1 = 1.
• Jos negatiivinen merkki edeltää ryhmän symbolia, se peruutetaan sijoittamalla sisällön merkki, esimerkiksi: - (−3 + 5 −1) = 3 - 5 + 1 = −1.
• Kun on yhdistetty summa-, vähennys-, kertolasku- ja jakotoimenpiteitä, assosiatiivisia ja jakautuvia ominaisuuksia voidaan käyttää mukavuuteen.

Ratkaisut

a) 10 + 10

Ratkaisu: 20

b) (-8) + (-3)

Ratkaisu: -11

c) (3) + (-10) 

Ratkaisu: -7

d) (5) x (-3)

Ratkaisu: -15

e) (-10) x (-10)

Ratkaisu: 100

f) (18) ÷ (-3)

Ratkaisu: -6

G) (-10) ÷ (-2)

Ratkaisu: 5

h) 4 - ( - 7 + 9)

Ratkaisu: 4 - ( - 7 + 9) = 4 + 7 - 9 = 11 - 9 = 2