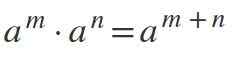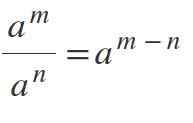Eksponenttien laki

Mitkä ovat eksponenttien lait?

Se Eksponenttien laki He ovat niitä, jotka koskevat tätä numeroa, joka osoittaa kuinka monta kertaa perusluku on kerrottava itsestään. Eksponentit tunnetaan myös voimina. Potentiaatio on matemaattinen toimenpide, jonka muodostavat pohja (a), eksponentti (m) ja voima (b), mikä on operaation tulos.

Eksponentteja käytetään yleensä, kun käytetään erittäin suuria määriä, koska nämä eivät ole muuta kuin lyhenteet, jotka edustavat saman lukumäärän kertomista tietyn määrän kertoja. Eksponentit voivat olla sekä positiivisia että negatiivisia.

Mitkä ovat matemaattisten operaatioiden eksponentit?

Kuten edellä todettiin, eksponentit ovat lyhennetty muoto, joka edustaa numeroiden kertomista itselleen, missä eksponentti liittyy vain vasempaan numeroon. Esimerkiksi:

2³ = 2*2*2 = 8

Tällöin numero 2 on tehon pohja, joka kerrotaan kolme kertaa, kuten eksponentti on osoittanut, joka sijaitsee pohjan oikeassa yläkulmassa. Ilmaisun lukemiseen on erilaisia ​​tapoja: 2 korotettua 3 tai 2 nostettuun kuutioon.

Eksponentit osoittavat myös, kuinka monta kertaa voidaan jakaa, ja tämän operaation erottamiseksi kertolaskulla on miinus (-) -merkki itsessään (se on negatiivinen), mikä tarkoittaa, että eksponentti on nimittäjässä. murto -osa. Esimerkiksi:

2^{- 4} = 1/2*2*2*2 = 1/16

Tätä ei pidä sekoittaa tapaukseen, jossa emäs on negatiivinen, koska se riippuu siitä, onko eksponentti tasainen vai pariton selvittääkseen, onko voima positiivinen vai negatiivinen. Siten sinun täytyy:

- Jos eksponentti on tasainen, voima on positiivinen. Esimerkiksi:

(-7)² = -7 _* -7 = 49.

- Jos eksponentti on outoa, voima on negatiivinen. Esimerkiksi:

(-2)⁵ = (-2)*(-2)*(-2)*(-2)*(-2) = -32.

On erityistapaus, jossa jos eksponentti on yhtä suuri kuin 0, teho on yhtä suuri kuin 1. On myös mahdollista, että pohja on 0; Tällöin eksponentista riippuen valtaa ei ole määritelty tai ei.

Matemaattisten operaatioiden suorittamiseksi eksponenttien kanssa on välttämätöntä.

Mitkä ovat eksponenttien lait?

Ensimmäinen laki: Eksponenttivoima yhtä suuri kuin 1

Kun eksponentti on 1, tulos on sama arvo kuin pohja: a¹ = a.

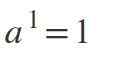
Esimerkit

9¹ = 9.

22¹ = 22.

895¹ = 895.

Toinen laki: Eksponenttivoima yhtä suuri kuin 0

Kun eksponentti on 0, jos pohja eroaa nollasta, tulos on: a^{0 -} = 1.

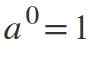
Esimerkit

1^{0 -} = 1.

323^{0 -}= 1.

1095^{0 -} = 1.

Kolmas laki: Negatiivinen eksponentti

Koska eksponentti on negatiivinen, tulos on murto -osa, jossa valta on nimittäjä. Esimerkiksi, jos m on positiivinen, niin^-m = 1/a^m.

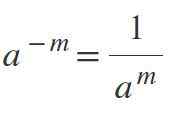
Esimerkit

- 3^-1 = 1/3.

- 6^-2 = 1/6² = 1/36.

- 8^-3 = 1/8³ = 1/512.

Neljäs laki: tasavertaisten voimien kertominen samalla tavalla

Kerrota voimia, joissa emäkset ovat samat ja erilaiset kuin 0, pohja ylläpidetään ja eksponentit lisätään: a^m _* -llaⁿ = a^m+n.    

Esimerkit

- 4⁴ _* 4³ = 4⁴⁺³ = 4⁷

- 8¹ _* 8⁴ = 8¹⁺⁴ = 8⁵

- 2² _* 2⁹ = 2²⁺⁹ = 2^yksitoista

Viides laki: Power Division kanssa samalla tukikohdalla

Voimien jakamiseksi, joissa emäkset ovat samat ja erilaiset kuin 0, pohja ylläpidetään ja eksponentit vähennetään seuraavasti: a^m /ⁿ = a^M-N.    

Esimerkit

- 9² / 9¹ = 9 ^{(kaksikymmentäyksi)} = 9¹.

- 6^viisitoista / 6¹⁰ = 6 ^{(15 - 10)} = 6⁵.

- 49¹² / 49⁶ = 49 ^{(12 - 6)} = 49⁶.

Kuudes laki: Eri voimien kertominen eri pohjalla

Tässä laissa on päinvastoin kuin se, joka ilmaistaan ​​neljännellä; Eli jos sinulla on erilaisia ​​emäksiä, mutta samoilla eksponenteilla, emäkset kerrotaan ja eksponentti ylläpidetään: a^m _* b -^m = (a_*b) ^m.

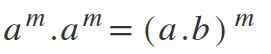
Esimerkit

- 10² _* kaksikymmentä² = (10 _* kaksikymmentä)² = 200².

- Neljä viisi^yksitoista _* 9^yksitoista = (45*9)^{11 =} 405^yksitoista.

Toinen tapa edustaa tätä lakia on, kun kertolasku on korkea voimalle. Siten eksponentti kuuluu jokaiseen termiin: (a_*b)^m= a^m_* b -^m.

Esimerkit

- (5_*8)⁴ = 5⁴ _* 8⁴ = 40⁴.

- (23 * 7)⁶ = 23⁶ _* 7⁶ = 161⁶.

Seitsemäs laki: Eri voimajako

Jos sinulla on erilaisia ​​emäksiä, mutta samoilla eksponenteilla emäkset jaetaan ja eksponentti ylläpidetään:^m / b^m = (a / b)^m.

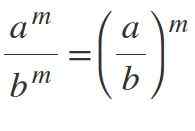
Esimerkit

- 30³ / 2³ = (30/2)³ = 15³.

- 440⁴ / 80⁴ = (440/80)⁴ = 5,5⁴.

Samoin, kun jako on korkea voimalle, eksponentti kuuluu jokaiseen termiin: (A / b) ^m = a^m /b^m.

Esimerkit

- (8/4)⁸ = 8⁸ / 4⁸ = 2⁸.

- (25/5)² = 25² / 5² = 5².

On tapaus, jossa eksponentti on negatiivinen. Joten positiiviseksi osoittajan arvo on sijoitettu nimittäjän arvoon seuraavasti:

- (A / B)^-n = (b / a)ⁿ = bⁿ /ⁿ.

- (4/5) ^-9 = (5/4) ⁹ = 5⁹ / 4⁴.

Kahdeksas laki: vallan voima

Kun sinulla on voima, joka nostetaan toiseen voimaan -toisin sanoen kaksi eksponenttia samanaikaisesti -pohja ylläpidetään ja eksponentit moninkertaistuvat: (a^m-Aⁿ= a^m*n.

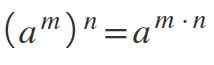
Esimerkit

- (8³-A² = 8 ^(3*2) = 8⁶.

- (13⁹-A³ = 13 ^(9*3) = 13²⁷.

- (238¹⁰-A¹² = 238^{(10 * 12)} = 238¹²⁰.

Yhdeksäs laki: murto -eksponentti

Jos teholla on eksponentti murto-osa, se ratkaistaan ​​muuttamalla se N-Esima-juureksi, jossa numeraattori pysyy eksponenttina ja nimittäjä edustaa juurihakemistoa:

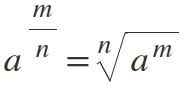
Esimerkki

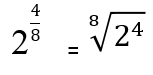
Ratkaisut

Harjoitus 1

Laske toiminnot, joilla on erilaiset perusteet:

2⁴ _* 4⁴ / 8².

Ratkaisu

Exponenttien sääntöjen soveltamisessa pohjat kerrotaan osoitimessa ja eksponentti ylläpidetään, kuten tämä:

2⁴ _* 4⁴ / 8²= (2_*4)⁴ / 8²  = 8⁴ / 8²

Nyt koska emäksiä on yhtä suuria, mutta erilaisilla eksponenteilla pohja ylläpidetään ja eksponentit vähennetään:

 8⁴ / 8² = 8^{(4 - 2)} = 8²

Harjoitus 2

Laske korkeat voimat toiseen voimaan:

(3²-A³ _* (2 _* 6⁵-A^-2 _* (2²-A³

Ratkaisu

Lakien soveltamisessa sinun on:

(3²-A³ _* (2 _* 6⁵-A^-2 _* (2²-A³

= 3⁶ _* 2^-2 _* 2^-10 _* 2⁶

= 3⁶ _* 2^{(-2) + (- 10)} _* 2⁶

= 3⁶ _*  2^-12 _* 2⁶

= 3⁶ _* 2^{(-12) + (6)}

= 3⁶ _* 2⁶

= (3_*2)⁶

= 6⁶

= 46.656

Viitteet

1. Aponte, g. (1998). Matematiikan perustiedot. Pearson -koulutus.
2. Corbalán, f. (1997). Arkielämään sovellettu matematiikka.
3. Jiménez, J. R -. (2009). Matematiikka 1. syyskuuta.
4. Max Peters, W. Lens. (1972). Algebra ja trigonometria.
5. Rees, P. K -k -. (1986). Palautus.