Tasaisesti kiihdytetyt suoraviivaiset liikkumisominaisuudet, kaavat

Hän tasaisesti kiihtynyt suoratoisto Se kulkee suoran linjan yli ja jossa matkapuhelin kasvaa tai vähentää nopeuttaan vakionopeudella. Tämä nopeus on suuruus, joka kuvaa rytmiä, jolla nopeus muuttuu ja jota kutsutaan kiihtyvyys.

Yhdenmukaisesti kiihdytetyn tai vaihtelevan suoraviivaisen liikkeen (MRUV) tapauksessa jatkuva kiihtyvyys on vastuussa nopeuden suuruuden muuttamisesta. Muun tyyppisissä liikkeissä kiihtyvyys pystyy myös muuttamaan suuntaa ja nopeuden tunnetta tai jopa muuttamaan suuntaa, kuten yhtenäisessä pyöreässä liikkeessä.

Kuvio 1. Nopeutetut liikkeet ovat yleisimpiä. Lähde: Pixabay.

Koska kiihtyvyys edustaa nopeuden muutosta ajan myötä, sen yksiköt kansainvälisessä järjestelmässä ovat m/s² (Meterit sekunneissa neliö). Kuten nopeus, kiihtyvyys voidaan myöntää positiivinen tai negatiivinen merkki, kun nopeus kasvaa tai vähenee.

Kiihtyvyys sanotaan +3 m/s² Se tarkoittaa, että jokaiselle kulkevalle sekunnille liikkuvan nopeuden nopeus kasvaa 3 m/s. Jos liikkeen alussa (t = 0) liikkuvan nopeuden oli +1 m/s, sekunnin kuluttua se on 4 m/s ja 2 sekunnin kuluttua se on 7 m/s.

Yhdenmukaisesti vaihtelevassa suoraviivaisen liikkeen aikana otetaan huomioon nopeuden vaihtelut, jotka liikkuvat objektit päivittäiset kokemukset. Se on realistisempi malli kuin yhtenäisen välittömän liikkeen malli. Silti se on edelleen melko rajallinen, koska se rajoittaa matkapuhelinta matkustamaan vain suoralla linjalla.

[TOC]

Ominaisuudet

Nämä ovat tasaisesti kiihdytetyn suorakulmaisen liikkeen pääominaisuudet:

-Liike kulkee aina suoraa linjaa pitkin.

-Mobiilin kiihtyvyys on vakio sekä suuruudessa että suunnassa ja merkityksessä.

-Mobiilinopeus kasvaa (tai vähenee) lineaarista.

-Kiihtyvyyden jälkeen -lla pysyy vakiona ajan myötä t, Sen suuruuskaavio ajan funktiona on suora. Kuviossa 2 esitetyssä esimerkissä viiva on sininen ja kiihtyvyysarvo luetaan pystysuoralla akselilla, suunnilleen +0.68 m/s².

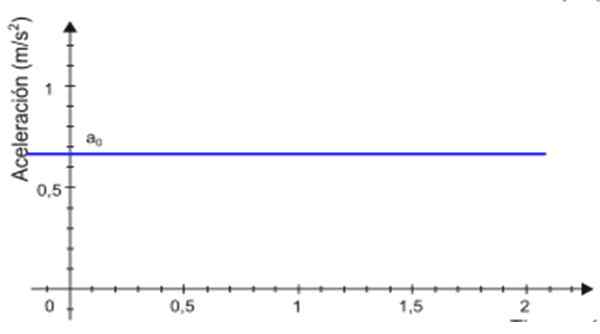Kuva 2. Kiihdytyskaavio ajan mukaan tasaisesti vaihtelevalle välittömälle väliaikaiselle liikkeelle. Lähde: Wikimedia Commons.

-Nopeuskaavio v noin t Se on suora viiva (vihreänä kuvassa 3), jonka kaltevuus vastaa mobiilia kiihtyvyyttä. Esimerkissä kaltevuus on positiivinen.

Se voi palvella sinua: boorinitride (BN): rakenne, ominaisuudet, hankkiminen, käyttö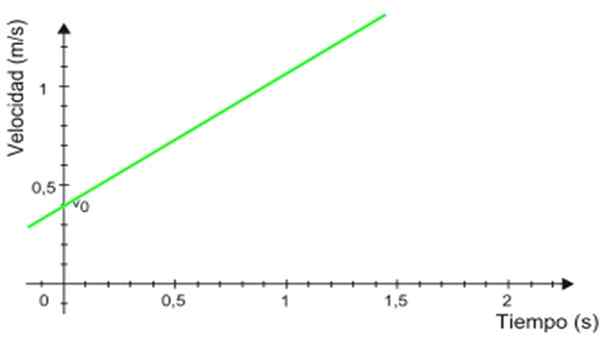 Kuva 3. Nopeuskaavio, joka perustuu ajanjaksoon tasaisesti vaihtelevalle suoraviivaiselle liikkeen päälle. Lähde: Wikimedia Commons.

-Leikkaus pystysuoralla akselilla osoittaa alkuperäisen nopeuden, tässä tapauksessa se on 0.4 m/s.

-Lopuksi X -asennon kaavio verrattuna ajan on kuvassa 4 punainen käyrä, joka on aina vertaus.

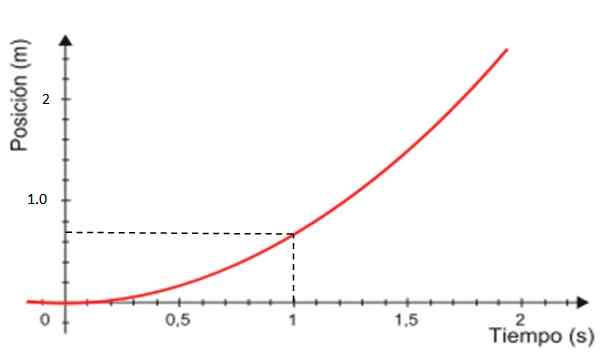Kuva 4. Aseman graafinen ajanjakson perusteella tasaisesti vaihtelevalle välitöntä liikkeen suhteen. Lähde: Modifioitu Wikimedia Commons.

Graafista V vs. kulunut etäisyys. t

Graafilla V vs. T, matkapuhelimen kuljettaman matkan laskenta on erittäin helppoa. Ajattu etäisyys vastaa linjan alla olevaa aluetta, joka sisältyy haluttuun aikaväliin.

Oletetaan, että haluat tietää, että haluat tietää matkan, jota matkapuhelin on kulkenut välillä 0 - 1 sekuntia. Käyttämällä tätä kuvaajaa, katso kuva 5.

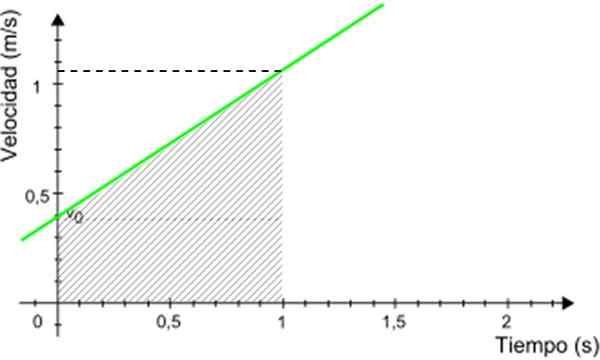Kuva 5. Kaavio matkapuhelimen kuljettaman matkan laskemiseksi. Lähde: Modifioitu Wikimedia Commons.

Etäisyys etsivät numeerisesti vastaavat varjostetun trapetsoidin aluetta kuvassa 3. Trapetsoidialue annetaan: (Tärkein pohja + vähäinen pohja) x korkeus/2

KÄYTETTY AIKAA = (0.4 + 1.05) x 1/2 m = 0.725 m

On myös mahdollista jakaa varjostettu alue kolmioon ja suorakulmioon, laskea vastaavat alueet ja lisätä ne. Kääntynyt etäisyys on positiivinen, vaikka hiukkas menee oikealle tai vasemmalle.

Kaavat ja yhtälöt

Sekä keskimääräisen kiihtyvyyden että välittömän kiihtyvyyden on sama arvo MRUV: ssä, siksi:

-Kiihtyvyys: -lla = vakio

Kun kiihtyvyys on yhtä suuri kuin 0, liike on tasainen suorakulmainen, koska nopeus olisi tässä tapauksessa vakio. Merkki -lla Se voi olla positiivinen tai negatiivinen.

Koska kiihtyvyys on viivan V kaltevuus versus t, yhtälö v (t) on:

-Nopeus ajasta riippuen: v (t) = v_jompikumpi + At

Missä v_jompikumpi Se on alkuperäinen liikkuvan nopeuden arvo

-Sijainti ajasta riippuen: x (t) = x_jompikumpi + v_jompikumpi T +½at² 

Kun aikaa ei ole saatavana, vaan sen sijaan on nopeuksia ja siirtymiä, on erittäin hyödyllinen yhtälö, joka saadaan puhdistamalla aika v (t) = v_jompikumpi + At ja sen korvaaminen viimeisessä yhtälössä. On noin:

Voi palvella sinua: potentiaalinen energia: ominaisuudet, tyypit, laskelmat ja esimerkit

-Yhtälö, joka ei sisällä aikaa: v² = v_jompikumpi² +2.-lla.Δx

Ratkaisut

Kinematiikkaharjoituksen ratkaisemisen yhteydessä on tärkeää varmistaa, että tilanne ehdotetaan käytettävään malliin sovittua. Esimerkiksi yhtenäisen suorakulmaisen liikkeen yhtälöt eivät ole voimassa nopeutettuun liikkeeseen.

Ja kiihdytetyn liikkeen osat eivät ole päteviä esimerkiksi pyöreän tai kaarevan liikkeen suhteen. Ensimmäinen näistä harjoituksista, jotka on ratkaistu alla. Sen ratkaisemiseksi on tarpeen siirtyä asianmukaiseen liikemalliin.

-Liikunta ratkaistiin 1

Saadakseen kaivon syvyyden, lapsi pudottaa kolikon ja aktivoi samalla sekuntikellonsa, joka pysähtyy tarkasti kuunnellessaan valuuttavallankaappausta vettä vastaan. Sen lukeminen oli 2.5 sekuntia. Tietäen, että äänen nopeus ilmassa on 340 m/s, laske kaivon syvyys.

Ratkaisu

Olla h Kaivon syvyys. Valuutta kulkee tämän etäisyyden vapaan putoamisen, tasaisesti vaihdetun pystysuuntaisen liikkeen, alkuperäisen nopeuden 0, koska valuutta pudotetaan ja jatkuva kiihtyvyys samaan kuin 9.8 m/s². Ota aikasi t_m Tehdessään tämän.

Kun valuutta törmää veden kanssa, napsautuksen aiheuttama ääni kulkee lapsen korvaan, joka pysäyttää sekuntikellon kuunnellessaan sitä. Ei ole syytä uskoa, että äänen nopeus muuttuu kiipeilyssä kaivoon, joten ääniliike on tasainen väliresisäinen. Ääni vie aikaa t_s päästä lapseen.

Valuutan liikkumisyhtälö:

H = ½.g.t_m ² = 4.9 t_m ²

Missä ne on korvattu x ja -lla edellisessä osassa annetun aseman yhtälöstä h ja g.

Äänen liikkeen yhtälö:

H = V_s . t_s = 340 T_s

Tämä on tuttu yhtälö Etäisyys = nopeus x aika. Näillä kahdella yhtälöllä on kolme tuntematonta: H, TM ja TS. Toisinaan on suhde, tiedetään, että kaikki vie 2.Siksi 5 sekuntia tapahtuu:

t_m + t_s = 2.5 s

Molempien yhtälöiden tasaaminen:

4.9 t_m ² = 340 T_s

Selvittää yksi kerralla ja korvaaminen:

4.9 t_m ²= 340.(2.5 - t_m-A

Kun kehitetään oikeanpuoleisen ja siirtävien termien termi, se saadaan:

Voi palvella sinua: Pystysuora laukaus: Kaavat, yhtälöt, esimerkit

4.9 t_m ²+340 T_m - 850 = 0

Tämä on toisen asteen yhtälö, jossa on kaksi ratkaisua: 2.416 ja -71.8. Positiivinen ratkaisu valitaan, mikä on järkevää, koska aika ei voi olla negatiivinen ja joka tapauksessa sen on oltava alle 2.5 sekuntia. Tällä kertaa se saadaan korvaamalla kaivon syvyys:

4.9 t_m ²= 4.9 x 2.416² M = 28.6 m

-Liikunta ratkaistiin 2

Auto, joka kulkee nopeudella 90 km/h, lähestyy poikittaista kadua liikennevalolla. Kun siellä on 70 m, keltainen valo kytketään päälle, jonka kesto on 4 sekuntia. Liikennevalon ja seuraavan kulman välinen etäisyys on 50 m.

Kuljettajalla on nämä kaksi vaihtoehtoa: a) seiso - 4 m/s² tai b) kiihdyttää + 2 m/s². Mikä kahdesta vaihtoehdoista antaa kuljettajalle lopettaa tai ylittää koko kadun ennen kuin valo muuttuu punaiseksi?

Ratkaisu

Kuljettajan alkuperäinen sijainti on x = 0 juuri kun hän näkee keltaisen valon. On tärkeää muuntaa yksiköt oikein: 90 km/h on 25 m/s.

Vaihtoehdon a) mukaan 4 sekunnissa, että keltainen valo kestää kuljettajan matkustaminen:

x (t) = v_jompikumpi T +½at²= 25.4 -½.(-4).4²M = 68 m (2 metriä ennen liikennevaloa)

Analysointi Vaihtoehto b) Sinulla on:

x (t) = v_jompikumpi T +½at²= 25.T +½.2.t²

Kun keltainen valo kestää, kuljettaja kulkee tällä tavalla:

x = 25.4 +½.2.4²M = 116 m

Mutta 116 m on pienempi kuin käytettävissä oleva etäisyys seuraavan nurkkaan saavuttamiseksi, joka on 70 + 50 m = 120 m, siksi se ei ylitä koko katua ennen kuin punainen valo on kytketty päälle. Suositeltu toiminta on pysähtyä ja pysyä 2 metrin päässä liikennevalosta.

Sovellukset

Joka päivä ihmiset kokevat kiihtyvyyden vaikutukset: kun he matkustavat autolla tai linja -autolla, koska heidän on jatkuvasti lopetettava ja kiihdytettävä mukauttaakseen marssin tien esteisiin. Kiihtyvyys on myös kokenut, kun se menee ylös tai alas hississä.

Hauska puistot ovat sivustoja, joissa ihmiset maksavat kokea kiihtyvyyden vaikutukset ja pitää hauskaa.

Luonnossa havaitaan tasaisesti monipuolinen suoraviivainen liike, kun esine pudotetaan vapaasti tai kun se heitetään pystysuoraan ja sen odotetaan palaavan maahan. Jos ilmankestävyys on halveksittu, kiihtyvyyden arvo on painovoima: 9.8 m/s2.

Viitteet

1. Bauer, W. 2011. Fysiikka tekniikkaan ja tieteisiin. Osa 1. MC Graw Hill.40-45.
2. Figueroa, D. Fyysinen sarja tiedettä ja tekniikkaa. Osa 3. Painos. Kinematiikka. 69-85.
3. Giancoli, D.  Fysiikka: sovellusten periaatteet. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Käsitteellinen fysiikka. 5^th. Ed. Pearson. 14-18.
5. Kirkpatrick, L. 2007. Fysiikka: Katsaus maailmaan. 6^ta Lyhennetty painos. Cengage -oppiminen. 15-19.
6. Wilson, J. 2011. Fysiikka 10. Pearson -koulutus. 116-119