Satunnainen näytteenottomenetelmä, edut, haitat, esimerkit

Hän satunnainen näytteenotto Se on tapa valita tilastollisesti edustava otos tietystä populaatiosta. Osa periaatteesta, että jokaisella näytteen elementillä on oltava sama todennäköisyys valita.

Arvonta on esimerkki satunnaisesta näytteenotosta, jossa jokaiselle osallistujien populaation jäsenelle annetaan numero. Arpajapalkintojen (näyte) vastaavien numeroiden valitseminen käytetään jonkin verran satunnaista tekniikkaa, esimerkiksi poiste postilaatikosta.

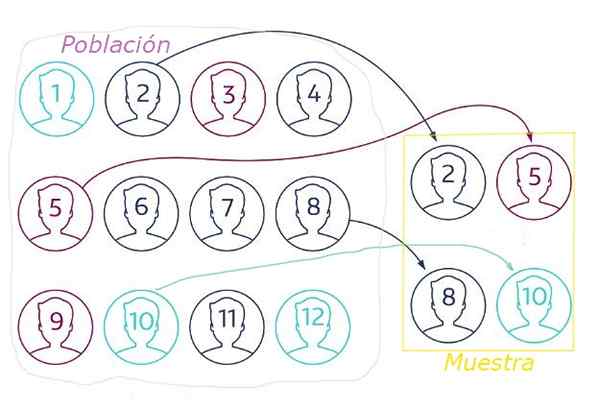Kuvio 1. Satunnaisessa näytteessä näyte uutetaan satunnaispopulaatiosta jonkin tekniikan avulla, joka varmistaa, että kaikilla elementeillä on sama todennäköisyys valita. Lähde: Netquest.com.

Satunnaisessa näytteessä se on välttämätöntä.

[TOC]

Näytteen koko

On kaavoja näytteen oikean koon määrittämiseksi. Tärkein huomioitava tekijä on se, tiedetäänkö populaation koko vai ei. Katsotaanpa kaavoja näytteen koon määrittämiseksi:

Tapaus 1: Väestön kokoa ei tunneta

Kun populaation kokoa ei tunneta, on mahdollista valita riittävä N -näyte, jotta voidaan määrittää, onko tietty hypoteesi totta vai väärä.

Tätä varten käytetään seuraavaa kaavaa:

n = (z² P q)/(e²-A

Missä:

-P on todennäköisyys, että hypoteesi on totta.

-Q on todennäköisyys, että se ei ole, siksi q = 1 - p.

-E on virhemarginaali, esimerkiksi 5%: n virheellä on marginaali E = 0,05. 

-Z liittyy tutkimuksen edellyttämään luottamustasoon.

Voi palvella sinua: Normaali jakauma: kaava, ominaisuudet, esimerkki, liikunta

Normaalissa jakautumisessa tyypillisellä (tai normalisoituna) 90%: n luottamustasolla on Z = 1 645, koska todennäköisyys, että tulos on välillä -1 645σ ja +1 645σ, on 90%, missä σ on keskihajonta.

Luottamustasot ja niiden vastaavat Z -arvot 

1.- 50%: n luotettavuustaso vastaa Z = 0,675.

2.- 68.3%: n luotettavuustaso vastaa z = 1.

3.- 90%: n luotettavuustaso, joka vastaa Z = 1 645.

4.- 95%: n luotettavuustaso vastaa Z = 1,96

5.- 95,5%: n luottamustaso vastaa Z = 2.

6.- 99,7%: n luotettavuustaso vastaa Z = 3.

Esimerkki, jossa tätä kaavaa voidaan soveltaa, olisi tutkimuksessa rannan kivien keskimääräisen painon määrittämiseksi.

Kaikkien rannan kivien tutkiminen ja punnitseminen ei selvästikään ole mahdollista, joten se on kätevä.

Kuva 2. Rannan kivien ominaisuuksien tutkimiseksi on tarpeen valita satunnainen näyte, jolla on edustava määrä niitä. (Lähde: Pixabay)

Tapaus 2: Väestön koko tunnetaan

Kun tiedetään tietyn populaation (tai maailmankaikkeuden) muodostavien elementtien lukumäärä n, jos haluat valita yksinkertaisella satunnaisella näytteellä tilastollisesti merkitsevää näytteen, tämä on kaava: 

n = (z²p q n)/(n e² + Z -z²P q)

Missä:

-Z on luottamuksen tasoon liittyvä kerroin.

-P on hypoteesin onnistumisen todennäköisyys.

-Q on hypoteesin epäonnistumisen todennäköisyys, p + q = 1.

-N on koko väestön koko.

-E on tutkimustuloksen suhteellinen virhe.

Esimerkit

Näytteiden poimimismenetelmä riippuu paljon tutkimuksen tyypistä. Siksi satunnaisessa näytteessä on lukemattomia sovelluksia:

Voi palvella sinua: ryhmittelyn merkkejä

Tutkimukset ja kyselylomakkeet

Esimerkiksi puhelintutkimuksissa ihmiset valitaan kuulemaan satunnaislukugeneraattorilla, jota voidaan soveltaa tutkittavaan alueeseen.

Jos haluat soveltaa kyselylomaketta suuren yrityksen työntekijöille, vastaajien valintaa voidaan käyttää työntekijän numeronsa tai henkilöllisyyskortin numeron kautta.

Tämä luku on myös valittava satunnaisesti, käyttämällä esimerkiksi satunnaislukugeneraattoria.

Kuva 3. Kyselylomaketta voidaan soveltaa satunnaisesti valitsemalla osallistujia. Lähde: Pixabay.

QA

Jos tutkimus on koneen valmistamilla osilla, osat on valittava satunnaisesti, mutta eri päiväaikoina tehdyt erät tai eri päivinä tai viikkoina.

Edut

Yksinkertainen satunnainen näytteenotto:

- Se mahdollistaa tilastollisen tutkimuksen kustannusten vähentämisen, koska koko väestöä ei tarvitse tutkia tilastollisesti luotettavien tulosten saamiseksi halutulla luottamustasolla ja tutkimuksessa vaadittavan virheen tasolla.

- Vältä puolueellisuutta: Koska tutkittavien elementtien valinta on täysin satunnaisesti, tutkimus heijastaa uskollisesti väestön ominaisuuksia, vaikka vain osaa tutkittiin vain osaa.

Haitat

- Menetelmä ei ole riittävä tapauksissa, joissa haluat tietää mieltymykset eri ryhmissä tai populaatiokerroksissa.

Tässä tapauksessa on edullista määrittää aiemmin ryhmät tai segmentit, joilla tutkimus tehdään. Kun kerrokset tai ryhmät on määritelty, niin jos jokaiselle on kätevää käyttää satunnaista näytteenottoa.

- On hyvin epätodennäköistä, että saadaan vähemmistösektoreita koskevat tiedot, joista on joskus tarpeen tietää niiden ominaisuudet.

Voi palvella sinua: Simpson -sääntö: kaava, esittely, esimerkit, harjoitukset

Esimerkiksi, jos kyseessä on kalliiden tuotteiden kampanja, on tarpeen tietää rikkaimpien vähemmistösektorien mieltymykset.

Liikuntaa

Haluamme tutkia väestön suosimista Colan colan avulla, mutta siinä populaatiossa ei ole aikaisempaa tutkimusta, josta sen koko ei ole tiedossa.

Toisaalta näytteen on oltava edustava vähimmäisluotettavuustaso 90% ja johtopäätösten on oltava prosentuaalinen virhe 2%.

-Kuinka määrittää näytteen S -koko?

-Mikä olisi näytteen koko, jos virhemarginaali tehdään 5%: iin?

Ratkaisu

Koska populaation koko ei ole tiedossa, näytteen koon määrittämiseksi käytetään yllä annettua:

n = (z²P q)/(e²-A

Oletamme.

Toisaalta, koska tutkimustuloksella on oltava alle 2%: n prosentuaalinen virhe, suhteellinen virhe on 0,02.

Lopuksi arvo Z = 1 645 tuottaa 90%: n luottamustason.

Lyhyesti sanottuna, sinulla on seuraavat arvot:

Z = 1 645

P = 0,5

Q = 0,5

E = 0,02

Näiden tietojen kanssa laskennan vähimmäiskoko:

N = (1 645² 0,5 0,5)/(0,02²) = 1691,3

Tämä tarkoittaa, että vaaditulla virhemarginaalilla ja valitun luottamuksen tasolla on oltava vähintään 1692 yksilön vastaajien näyte, joka on valittu yksinkertaisella satunnaisella näytteellä.

Jos siirryt virhemarginaalista 2%: sta 5%: iin, uusi otoskoko on:

N = (1 645² 0,5 0,5)/(0,05²) = 271

Mikä on huomattavasti pienempi lukumäärä yksilöitä. Yhteenvetona voidaan todeta, että otoskoko on erittäin herkkä tutkimuksen halutulle marginaalille.

Viitteet

1. Berenson, m. 1985.Tilastot hallinnosta ja taloudesta, käsitteistä ja sovelluksista. Amerikanvälinen toimitus.
2. Tilastot. Satunnainen näytteenotto. Otettu: Encyclopediaconomica.com.
3. Tilastot. Näytteenotto. Palautettu: Tilastot.Matto.Tukko.MX.
4. Tutkittava. Satunnainen näytteenotto. Palautettu: Exploreble.com.
5. Moore, D. 2005. Perustilastot. Toinen. Painos.
6. Netquest. Satunnainen näytteenotto. Palautettu: Netquest.com.
7. Wikipedia. Tilastollinen näyte. Haettu: vuonna.Wikipedia.org