Vastakkaiset kulmat kärkikengellä (ratkaistu harjoittelu)

Se Vastakkaiset kulmat kärjen vieressä Ne ovat niitä, jotka täyttävät seuraavat: yhden sivut ovat toisen kulman sivujen pidentymisiä. Hän Peruslause Väkepisteiden vastakkaisista kulmista sanotaan: kahdella kärkipisteen vastustamalla kulmalla on sama mitta.

Monta kertaa kieltä väärin sanomalla, että kärkipisteen vastustamat kulmat ovat samat, mikä ei ole oikein. Se, että kahdella kulmalla on sama mitta, ei tarkoita, että ne ovat yhtä suuret. Se on kuin sanoisi, että kaksi lasta, joilla on sama korkeus, ovat yhtä suuret.

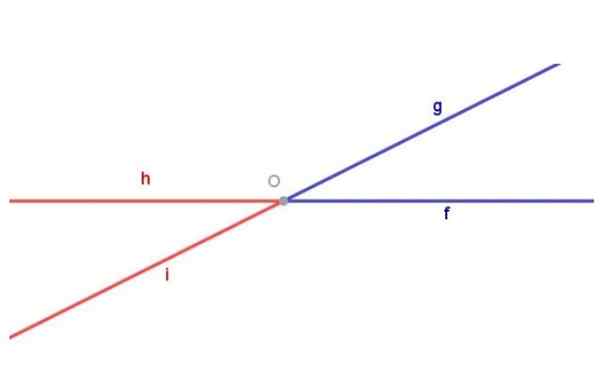
Kuvio 1. Vastakkaiset kulmat kärjessä. Valmistaja: Fanny Zapata.

Muista, että kulma on määritelty geometriseksi hahmoksi, joka koostuu kahdesta puolijohdosta, jolla on sama alkuperää.

Kuvio 1 näyttää kulman SUMU (Sininen) koostuu puoliksi rekrytoinnista [Of) ja puoliksi [OG) yleinen JOMPIKUMPI. Kuvio 1 näyttää myös kulman Hoi (punainen) koostuu puoliksi [Kuulin) ja puoliksi [VAI NIIN) Molemmat alkuperällä JOMPIKUMPI. 

Kaksi vastakkaista kulmaa kärjessä ovat kaksi erilaista geometrista lukua. Tämän korostamiseksi kuvassa 1 kulma on värillinen SUMU Sininen, kun taas kulma Hoi Hän on värillinen punainen. 

Kuvion 1 siniset ja punaiset kulmat vastustavat kärkipistettä, koska: puoliksi oikea [Of) Sinisen kulman on puoliksi oikeanpuoleisen pidennys [VAI NIIN) punaisesta kulmasta ja puoliksi [OG) Sinisen kulman on puoliksi oikeanpuoleisen pidennys [Kuulin) punaisesta kulmasta.

[TOC]

Tärkeät käsitteet kulmista

Kulman sivut ja kärkipisteet

Geometrinen hahmo, joka koostuu kahdesta puolijohdosta, jolla on yhteinen alkuperää, on kulma. Seuraava kuva näyttää kulman Poq muodostettu kahdella puoliksi oikealla [OP) ja [O Q) yleinen JOMPIKUMPI:

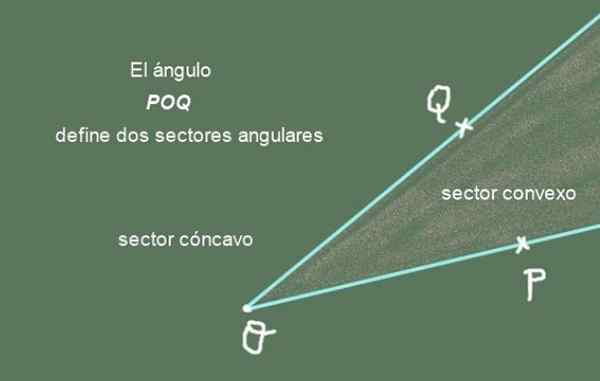Kuva 2. POQ -kulma määrittelee kaksi kulmalaista. Valmistaja: f. Zapata.

Puoliksi [OP) ja [O Q) ovat kulman sivut Poq, kun taas yhteinen kohta tai sitä kutsutaan Kulman vértice.

Voi palvella sinua: Sturges -sääntö

Kulma -ala: Kulma jakaa tason, joka sisältää sen kahteen kulma -sektoriin. Yksi niistä on kupera kulma -ala ja toinen on kovera kulma -ala. Kahden sektorin liitto antaa täyden lentokoneen.

Kuvio 2 näyttää kulmassa Poq ja sen kaksi kulma -alaa. Kukkas kulma -ala on se, jolla on terävä muoto, kun taas kovera on tason kulma -ala, joka puuttuu kupera sektorille.

Kulmat, jotka on muodostettu kahdella viivalla, jotka on leikattu

Kaksi tason riviä, jotka sieppataan neljä kulmaa ja jaa taso neljään kulma -alaan.

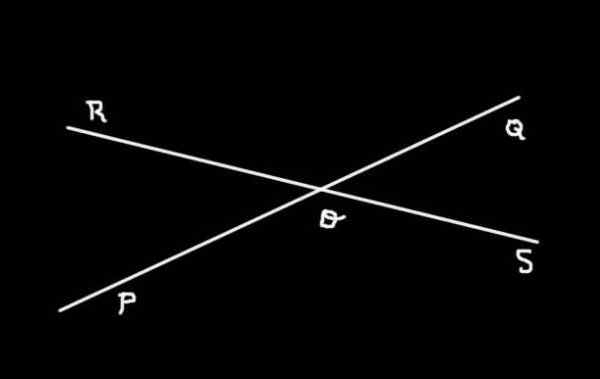Kuva 3. Linjat (PQ) ja (Rs) siepataan O- ja Form 4 -kulmissa. Valmistaja: f. Zapata.

Kuvio 3 näyttää kaksi viivaa (PQ) ja (RS) pysäytetty jhk JOMPIKUMPI. Siellä voit nähdä, että neljä kulmaa on määritetty:

-Sotilas, Quor, Ryöstää ja Postia

Kulmat Sotilas ja Quor, Quor ja Ryöstö ja Postia, Postia ja Sotilas are  viereiset kulmat keskenään, kun Sotilas ja Ryöstää Heitä vastustaa kärki. He ovat myös Vastakkaiset kulmat kärjen vieressä Kulmat Quor ja Postia.

Kohtisuoraviivat ja suora kulma

Kaksi kuivausviivaa (suorat viivat leikkaavat) ovat Kohtisuorat suorat linjat Jos ne määrittävät neljä saman mittaisen kulma -sektoria. Jos kukin neljästä sektorista on symmetrisiä viereisen kulma -alan kanssa, niin heillä on sama mitta.

Kumpaakin kulmasta, jotka määrittävät kaksi kohtisuoraa viivaa, kutsutaan oikea kulma. Kaikilla suorilla kulmilla on sama mitta.

Puoliksi -sarja samalla viivalla ja tasaisella kulmalla

Annetaan viiva ja piste sen, kaksi puolijohdetta on määritelty. Nämä kaksi puolijuoksua määrittelevät kaksi litteät kulmat.

Kuviossa 3 viiva voidaan havaita (RS) Ja kohta JOMPIKUMPI joka kuuluu (RS). Kulma Sora Se on tasainen kulma. Voidaan myös vahvistaa, että kulma Ros Se on tasainen kulma. Kaikilla litteillä kulmilla on sama mitta.

Voi palvella sinua: Clausurative omaisuus

Nollakulma ja täysi kulma

Yksi puoliksi recreational määrittelee kaksi kulmaa: yksi niistä kuperassa kulmektorissa on nollakulma Ja toinen, koveran kulma -ala on täysi kulma. Kuvassa 3 nollakulma SOS ja täysi kulma SOS. 

Mittaus 

On olemassa kaksi numeerista järjestelmää, joita käytetään usein kulman mittaamiseen. 

Yksi niistä on seksuaalinen järjestelmä, ts. Se on muinaisen Mesopotamian kulttuurien perintö. Muut kulmien mittausjärjestelmä on Radián -järjestelmä, joka perustuu numeroon π (PI) ja on geometrian kehittäneiden muinaiskreikkalaisten viisaiden perintö.

Seksuaalinen järjestelmä

NULL -kulma: Seksuaalisessa järjestelmässä nollakulma mittaa 0º (nolla astetta).

Täysi kulma: 360º: n mitta on määritetty (kolmesataa kuusikymmentä astetta).

Litteä kulma: Seksuaalisessa järjestelmässä tasainen kulma mittaa 180º (sata kahdeksankymmentä astetta).

Oikea kulma: Kaksi kohtisuoraa viivaa jakaa taso neljään yhtä suureen mittaan, nimeltään Suorat kulmat. Oikeakulman mitta on neljäsosa koko kulmasta, eli 90º (yhdeksänkymmentä astetta).

Kuljetin tai goniometri

Kuljetin on väline, jota käytetään kulmien mittaamiseen. Se koostuu puolipyöreästä (yleensä läpinäkyvästä muovista), joka on jaettu 180 kulmaosaan. Puolipyöränä muodostaa tasaisen kulman, niin mitta kahden peräkkäisen osan välillä on 1.

Goniometri on samanlainen kuin kuljettaja ja koostuu ympyrästä, joka on jaettu 360 kulmaosaan.

Kulma, jonka sivut alkavat goniometrin keskeltä, sieppaa kaksi sektoria ja kyseisen kulman mitta asteina on yhtä suuri kuin kahden sieppatun sektorin välisten osien lukumäärä n, tässä tapauksessa toimenpide on nro (lukee ““ “Ene -asteet”).

Se voi palvella sinua: neliö senttimetriä neliömetriin (cm² - m²)

Välikerroksen vastakkaisten kulmien lause

Muodollisesti lause esitetään tällä tavalla:

Jos kärkipistettä vastustetaan kahta kulmaa, heillä on sama mitta.

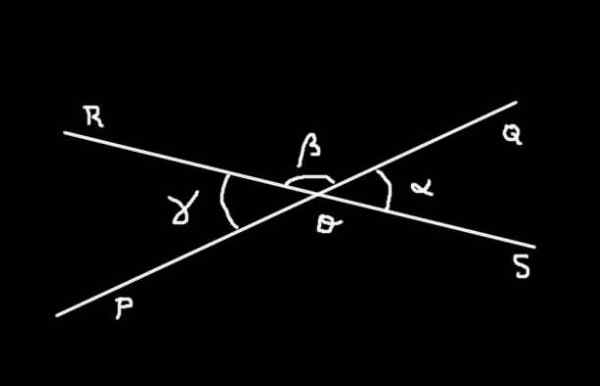Kuva 4. α, β ja y ovat SOQ-, QOR- ja ROP -kulmien mitat. Valmistaja: f. Zapata.

Esittely

Kulma Sotilas Sillä on α -mitta; kulma Quor Siinä on β -mitta ja kulma Ryöstää Sillä on γ -mitta. Kulman summa Sotilas lisää häntä Quor muodostaa tasainen kulma Sora mitta 180º.

Tuo on:

α + β = 180º

Toisaalta ja käyttämällä samaa päättelyä kulmien kanssa Quor ja Ryöstää Sinulla on:

β + γ = 180º

Jos tarkkailemme kahta aikaisempaa yhtälöä, ainoa tapa, jolla molemmat täyttyvät, on, että α on yhtä suuri kuin γ.

Kuten Sotilas Sillä on α -mitta ja kärkivalta vastustaa sitä Ryöstää mitta γ: n ja kuten α = y, päätellään, että kärjen vastustamilla kulmilla on sama mitta.

Liikuntaa

Viittauksessa kuvioon 4: Oletetaan, että β = 2 α. Löydä kulmien mitta Sotilas, Quor ja Ryöstää Seksuaalisesti.

Ratkaisu

Kuten kulman summa Sotilas lisää häntä Quor muodostaa tasainen kulma Sora Sinulla on:

α + β = 180º

Mutta he kertovat meille, että β = 2 α. Tämän β -arvon korvaamiseksi jäljellämme:

α + 2 α = 180º

Tarkoittaen:

3 α = 180º

Mikä tarkoittaa, että α on 180º: n kolmas osa:

α = (180º / 3) = 60º

Sitten Sotilas on α = 60º. Mitta Quor IS β = 2 α = 2*60º = 120º. Lopuksi Ryöstää vastustaa kärki Sotilas Sitten lauseen mukaan jo osoitettu, että heillä on sama mitta. Eli mitta Ryöstää on γ = α = 60º. 

Viitteet

1. Baldor, J. -Lla. 1973.Litteä ja avaruusgeometria. Keski -Amerikan kulttuuri-. 
2. Matemaattiset lait ja kaavat. Kulman mittausjärjestelmät. Haettu: Ingemecanica.com.
3. Wikipedia. Vastakkaiset kulmat kärjessä. Palautettu: on.Wikipedia.com
4. Wikipedia. Kuljettaja. Palautettu: on.Wikipedia.com
5. Zapata f. Goniometri: Historia, osat, toiminta. Haettu: Lifer.com