Kulmat ja kolmiot

Kulmat ja kolmiot ovat osa tasaista geometriaa. Suljettu

Mitkä ovat kulmat ja kolmiot?

Eräs kulma Se on koneen alue, joka on rajattu kahdella puoliksi varustetulla alueella, jolla on yhteinen lähtökohta. Tämä kohta tunnetaan nimellä kärki, kun taas puoliksi puolet. Toisaalta a kolmio Se on kolmen kulman ja kolmen sivun kuva, kolmella kärkipisteellä.

Puhumme ensin kulmista.

Kulmat

On olemassa useita tapoja merkitä kulmia: kreikkalaisten kirjaimien, kuten α, β, y, johon voidaan lisätä kehä -aksentti; isoilla kirjaimilla verhoiltuja tai pieniä kirjaimia, a, b, c, a, b, c; Numerot, kuten 1, 2, 3 ... tai kulmasymbolin käyttäminen.

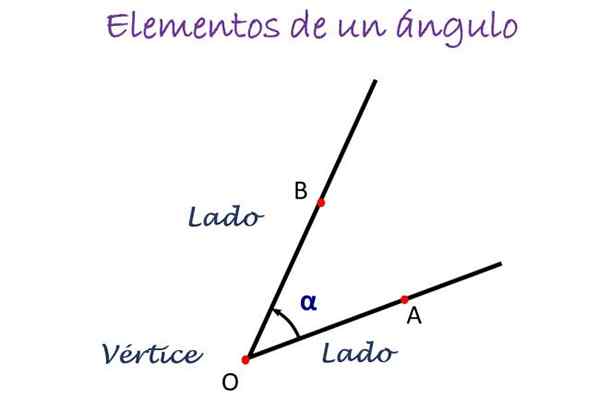Kulman pääelementit. Lähde: f. Zapata

Yllä olevassa kuvassa kulma mitataan sivulta A B: ksi, joka osoittaa nuolen suunnan, ja keskellä kirje, joka merkitsee kärkipistettä, joka on normaalisti tai. Kulma merkitään sitten nimellä ∠ AOB.

Kun kulma mitataan antihorarium -mielessä, A +-merkki osoitetaan mielivaltaisesti, ja jos se mitataan aikataulussa, merkki -erottaa ne.

Kulmien mitta suoritetaan kuljettajan avulla, joka koostuu puolipyöreästä muovilevystä, kuten alla olevasta. Puolipyöre on jaettu 180 yhtä suureen osaan, jokainen puhelu aste.

Mittaamiseksi kulman kärki tapahtuu samanaikaisesti kuljettajan keskipisteen kanssa, joka on osoitettu nuolella, ja alkupuolella yhdellä reunasta, sisäisestä tai ulkoisesta tai ulkoisesta. Viimeinen puoli leikkaa joitain kuljettajan merkkejä, tämä mitta on kulma.

Voi palvella sinua: Empiirinen sääntö: Kuinka soveltaa sitä, mihin se on, ratkaistut harjoitukset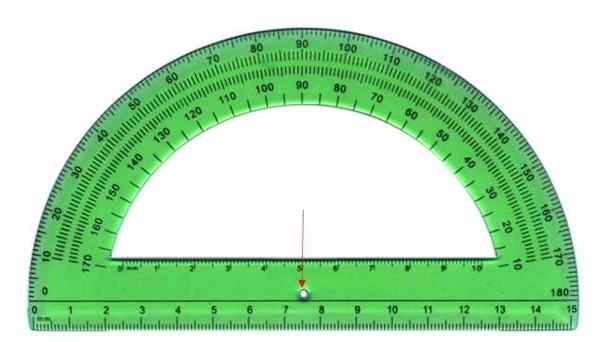Kuljetin on väline kulmien mittaamiseksi. Lähde: Wikimedia Commons

Kulmatyypit

Yksi käytetyimmistä kriteereistä kulmien luokittelemiseksi on sen mittauksen mukaan. Siksi kulma voi olla:

• Tyhjä, mittaa 0º.
• Terävä, jonka mitta on välillä 0 - 90º.
• Suoraan, Se mittaa tarkalleen 90º.
• Tylppä, Se on suurempi kuin 90º ja alle 180º.
• Tasainen, Sen mitta on yhtä suuri kuin 180º.
• Saattaa loppuun, edustaa täydellistä käännöstä ja mittaa 360º.

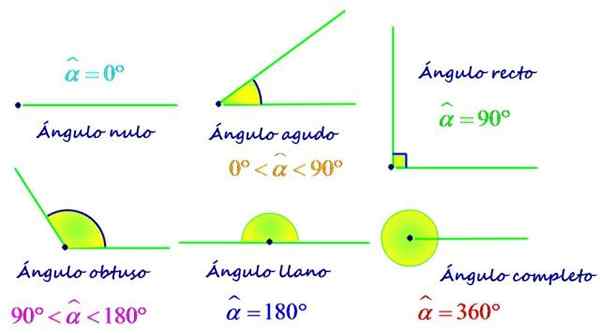Kulmatyypit mittasi mukaan. Lähde: f. Zapata.

Sen mitan ja tasaisen kulman välisen suhteen, joka on 180º, välisen suhteen mukaan kulmat voidaan myös luokitella seuraavasti:

• Kovera, Jos se mittaa alle 180º. Siksi akuutti, suorat ja otokkaat kulmat ovat koverat, koska sen mitta on aina alle 180º (katso yllä oleva kuva).
• Kupera, Jos mittasi on suurempi kuin 180º, koska kulmat 270º ja 360º.

Kulmat niiden toimenpiteiden summan mukaan ja heidän puolensa mukaan

Kaksi kulmaa ∠ A ja ∠ B voivat olla:

• Täydentävä, Jos sen mittojen summa on yhtä suuri kuin 90º.
• Lisä-, Kun lisätään vastaavat mitat, saadaan 180º.
• Konjugoitu, Jos tämä summa on yhtä suuri kuin 360º.

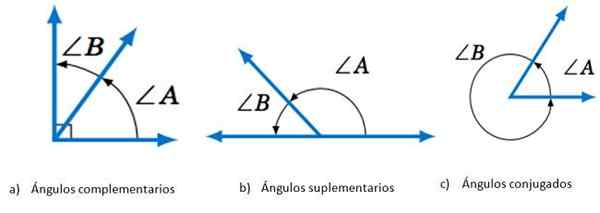Kulmat sen toimenpiteiden summan mukaisesti. Lähde: Matematiikka LibretTexts.

Niiden sivujen suhteen kaksi kulmaa voi olla:

• Rivissä, Kun kärkipisellä ja yhdellä puolella on yhteistä.
• Viereinen, Jos ne ovat peräkkäisiä, mutta ei -yleiset puolet ovat vastakkaisia, niin ne ovat myös lisätietoja.
• Vastapäätä kärki, Kun heillä on yhteinen kärki, ja kulmien sivut jatkuvat vastakkaiseen suuntaan.

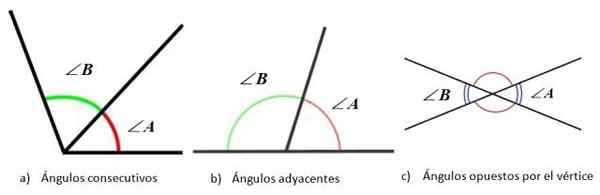Kulmat sen sivujen suhteellisen sijainnin mukaan. Lähde: f. Zapata

Kolmiot

Kolmio on litteä ja suljettu geometrinen hahmo, joka kuuluu monikulmioiden perheeseen, ja kolme sivua koostuu viivoista, jotka leikataan kaksi tai kaksi, ja ne tuottavat kolme kulmaa.

Se voi palvella sinua: Bijjective Function: Mikä se on, miten se tehdään, esimerkkejä, harjoituksia

Sen peruselementit ovat:

• Kärjet, jotka ovat edellä mainittujen viivojen risteyspisteitä.
• Puolet, Yhteensä 3 ja joka koostuu kärkipisteisiin yhdistävien linjojen segmenteistä.
• Sisäkulmat, Myös 3: n lukumäärä, jonka summa on aina yhtä suuri kuin 180º.

Yleensä sivut on merkitty pienillä latinalaisilla kirjaimilla, kärjillä, joissa on isoja kirjaimia ja kulmia, joilla on pienet grieous -kirjaimet, mutta myös muut merkinnät ovat mahdollisia.

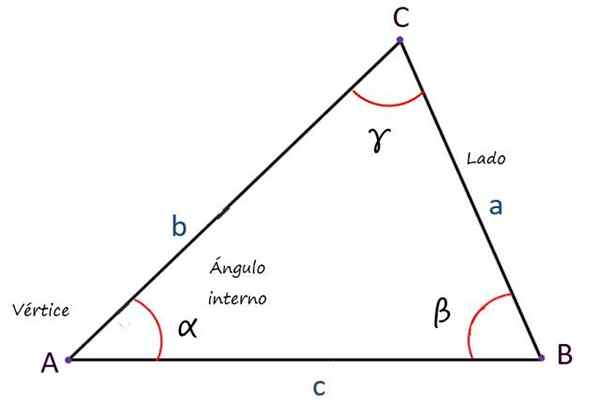Kolmion pääelementit. Lähde: f. Zapata

Kolmiotyypit

Kolmiot sen sivujen muodon mukaan

Tämän kriteerin mukaan kolmiot voivat olla:

• Tasasivut, Jos sen kolmella puolella on sama mitta.
• Sammutus, Kun vain kahdella sivulla on yhtä suuri, kun taas kolmas on erilainen.
• Skaaleeni, Jos kolme puolta ovat erikokoisia.

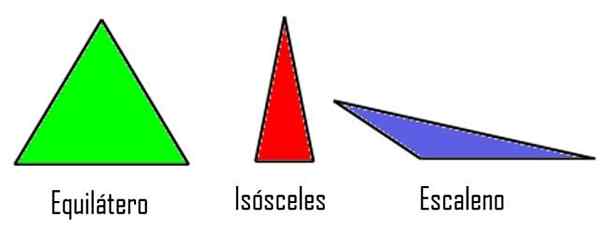Kolmiot heidän puolensa mukaan. Modifioitu Wikimedia Commons

Kolmiot sen sisäisten kulmien mukaan

Tämä kriteeri perustuu kolmion sisäisiin kulmatyyppeihin. Tämän mukaan kolmio voi olla:

• Akuttaa, Kun kolmion kolme sisäkulmaa ovat akuutteja.
• Suorakulmio, Jos kolmiossa on sisäinen mittakulma, joka on yhtä suuri kuin 90º.
• Tylppä, Yksi kolmion sisäkulmista on tylsä.

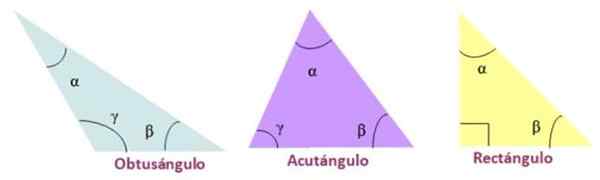Kolmiotyypit sisäisten kulmien mukaan. Lähde: f. Zapata

Merkittävät kolmiosegmentit

Minkä tahansa kolmion merkittävien segmenttien joukossa heillä on:

• Mediaani, segmentti, joka on suunnattu kärkipisteestä, suoraan vastakkaiselle puolelle.
• Mediarix, Se on segmentti, joka kuuluu sivulle kohtisuoraan, joka leikkaa kyseisen puolen keskipisteeseen.
• Puolustaja, Segmentti, joka jakaa sisäkulman kahteen yhtä suureen osaan ja joka ulottuu kulmaan vastakkaiselle puolelle.
• Korkeus, Segmentti kohtisuorassa sivuun nähden, joka ulottuu vastakkaiseen kärkeen.

Voi palvella sinua: LaGrange -interpolointi

Kolme väliainetta, kolme välilomista voidaan jäljittää ja niin edelleen.

Kolmiokeskukset

Missä tahansa kolmiossa seuraavat kohdat erottuvat (katso seuraava kuva):

• Baricentro g, myös joskus kutsutaan keskikohtaa Kolmiosta se on mediaanien leikkauspiste ja se on aina sisäinen kolmioon.
• Ortocenter h, kohta, jossa kolme korkeutta leikkaavat.
• Ympyrä tai, Se on lääketieteen leikkauspiste. Se löytyy kolmion ulkopuolelta, jos tämä on tylsää, kun taas suorakulmiokolmiossa tai vastaa samanaikaisesti hypotenusen keskipisteen.
• Kannustaa, kolmiokuvioiden leikkauspiste.
• Euler suora, Suoraan, joka yhdistää baricenterin, ortokeskuksen ja ympärysmittaisen, missä tahansa kolmiossa, joka ei ole tasa -arvoinen. On aina toteutettu, että HG -segmentin pituus on kaksinkertainen GO -segmentin pituus.

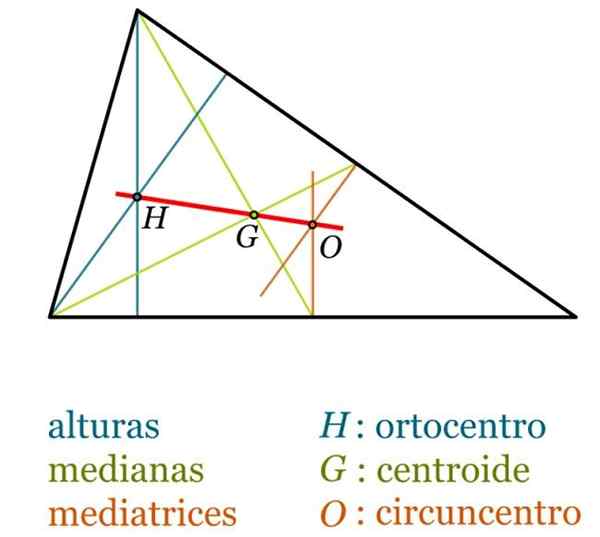Kolmion merkittävät kohdat ja segmentit. Lähde: Wikimedia Commons

Kolmion alue

Kolmion alueen A laskemiseksi käytetään seuraavaa kaavaa, yleinen:

A = pohja × korkeus / 2

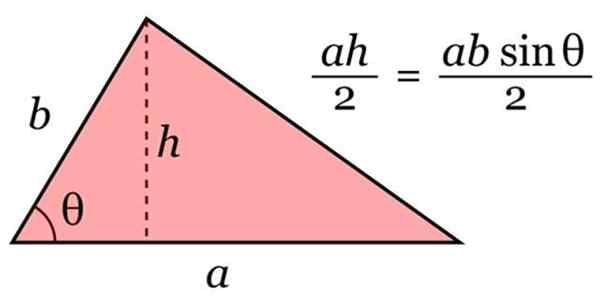Kolmion alue. Lähde: Wikimedia Commons

Herón -kaava

Kolmion kaikkien puolten pituuden, seuraava kaava, joka tunnetaan nimellä Herón -kaava, Antaa sinun löytää alue A:

Täällä kolmion sivut ovat A, B ja C, kun taas S_p onko hän puolijohde, toisin sanoen puolet kehästä p = a + b + c.

Viitteet

1. Alexander, D. 2013. Geometria. Viides. Painos. Cengage -oppiminen.
2. Kulmat. Matematiikka librettexts. Toipunut: matematiikka.Librettexts.org.
3. Jiménez, René. 2010. Matematiikka II (geometria ja trigonometria). Toinen. Painos. Pearson.
4. Maailmankaikkeuden kaavat. Kolmio. Toipunut: UniversOformulat.com.
5. Zapata, f. Kolmiot: historia, elementit, luokittelu, ominaisuudet. Haettu: Lifer.com.