Euler -numero tai numero e kuinka paljon on arvoinen, ominaisuudet, sovellukset

Hän Euler -numero tai numero E Se on hyvin tunnettu matemaattinen vakio, joka esiintyy usein lukuisissa tieteellisissä ja taloudellisissa sovelluksissa, yhdessä lukumäärän ja muiden tärkeiden lukujen kanssa matematiikassa.

Tieteellinen laskin heittää seuraavan arvon numerolle E:

Kuvio 1. Eulerin numero ilmestyy usein tieteessä. Lähde: f. Zapata.

E = 2.718281828…

Mutta esimerkiksi monia muita desimaaleja tunnetaan:

E = 2.71828182845904523536…

Ja nykyaikaiset tietokoneet ovat sallineet desimaalin biljoonan lukuun E.

Se on numero irrationaalinen, mikä tarkoittaa, että sillä on ääretön määrä desimaaleja ilman toistuvaa mallia (sekvenssi 1828 ilmestyy kahdesti alussa eikä enää toistu).

Ja se tarkoittaa myös sitä, että numeroa E ei voida saada kahden kokonaisluvun osamääräksi.

[TOC]

Historia

Numero ja Tutkija Jacques Bernoulli tunnisti hänet vuonna 1683, kun hän tutki yhdistetyn kiinnostuksen ongelmaa, mutta aiemmin hän oli epäsuorasti esiintynyt skotlantilaisen matemaatikon John Napierin teoksissa, jotka keksivät logaritmit vuodelle 1618.

Se oli Leonhard Euler vuonna 1727, joka antoi hänelle numeron E -nimen ja tutki intensiivisesti hänen ominaisuuksiaan. Siksi se tunnetaan myös nimellä Euler -numero ja myös luonnollinen perusta Neperian logaritmeille (eksponentti).

Kuinka paljon numero E on arvoinen?

Numero E Vale:

E = 2.71828182845904523536…

Suspensat tarkoittavat, että desimaalit ovat äärettömän määrän ja tosiasiassa miljoonat niistä tunnetaan nykyisillä tietokoneilla.

Numeron E esitykset

Seuraavassa kuvailemme E: n määrittelemiseksi on useita tapoja:

Numero E rajoituksena

Yksi eri tavoista, joilla luku E ilmaistaan, on se, jonka tutkija Bernoulli löysi hänen työstään yhdistelmäkohdasta:

Jossa sinun on tehtävä arvo n erittäin suuri määrä.

Se on helppo tarkistaa laskimen avulla, että milloin n Se on erittäin suuri, aikaisemmalla lausekkeella on taipumus ja annettu yllä.

Se voi palvella sinua: Bijjective Function: Mikä se on, miten se tehdään, esimerkkejä, harjoituksia

Tietysti voimme kysyä itseltämme, kuinka suuri se voidaan tehdä n, Joten yritämme esimerkiksi pyöreällä numerolla, kuten nämä:

n = 1000; 10.000 tai 100.000

Ensimmäisessä tapauksessa saat E = 2.7169239… . Toisessa E = 2.7181459… ja kolmannessa se on paljon lähempänä ja: 2.7182682. Voimme jo näyttää, että n = 1: llä.000.000 tai suurempi, lähestymistapa on vielä parempi.

Matemaattisella kielellä, tekemisen menettely n Se lähenee ja enemmän erittäin suurta arvoa, sitä kutsutaan äärettömyyttä Ja se on merkitty näin:

Äärettömyyden osoittamiseksi käytetään "∞" -symbolia.

Numero E summana

On myös mahdollista määritellä numero E tämän operaation kautta:

Nimittäjässä näkyvät luvut: 1, 2, 6, 24, 120 ... vastaavat operaatiota n!, missä:

n! = n. (N-1).(N-2). (N-3) ..

Ja määritelmän mukaan 0! = 1.

On helppo varmistaa, että mitä enemmän lisäyksiä lisätään, sitä suurempi luku saavutetaan ja.

Tehdään joitain testejä laskimen kanssa lisäämällä yhä enemmän lisäyksiä:

1 +1+ (1/2) + (1/6) = 2.71667

1 +1+ (1/2) + (1/6) + (1/24) = 2.75833

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) = 2.76667

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) + (1/720) = 2.71806

Mitä enemmän ehtoja ne lisätään summaan, sitä enemmän tulos on samanlainen kuin ja.

Matemaatikot suunnittelivat kompaktin merkinnän näille summille, joihin liittyy monia termejä, käyttämällä summamymbolia σ:

Tämä lauseke luetaan nimellä "n = 0: n summa 1: n äärettömyyteen n tekijän välillä".

Numero E geometrisesta näkökulmasta

Numerossa E on graafinen esitys, joka liittyy käyrän kaavion alla olevaan alueeseen:

y = 1/x

Kun X: n arvot ovat välillä 1 ja E, tämä alue on arvoinen 1, kuten seuraavassa kuvassa on esitetty:

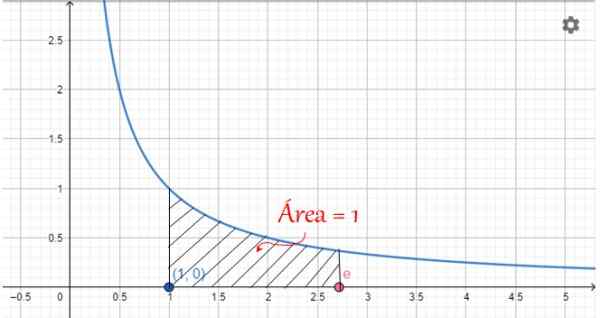Kuva 2. Numeron E graafinen esitys: Käyrän 1/x alla oleva alue, välillä x = 1 ja x = e kello. Lähde: f. Zapata.

Numero E Ominaisuudet

Jotkut numeron E ominaisuuksista ovat:

Voi palvella sinua: Kasvava toiminto: Kuinka tunnistaa se, esimerkkejä, harjoituksia

-Se on irrationaalista, toisin sanoen sitä ei voida saada yksinkertaisesti jakamalla kaksi kokonaisluku.

-Numero ja Se on myös a Transsendenttinen luku, mikä tarkoittaa sitä ja Se ei ole minkään polynomiyhtälön ratkaisu.

-Se liittyy neljään muuhun kuuluisaan lukuun matematiikan alalla, nimittäin: π, i, 1 ja 0, Eulerin identiteetin kautta:

ja^πi + 1 = 0

-Puhelut kompleksilukut voidaan ilmaista E: n kautta.

-Se muodostaa nykyään luonnollisten tai Neperian logaritmien perustan (John Napierin alkuperäinen määritelmä eroaa vähän).

-Se on ainoa luku, että sen neperian logaritmi on 1 arvoinen, eli:

 ln e = 1

Sovellukset

Tilastot

Luku E ilmestyy hyvin usein todennäköisyyden ja tilastojen alalla, joka esiintyy erilaisissa jakaumissa, kuten normaalissa tai Gaussin, Poissonin ja muiden jakautumisessa.

Tekniikka

Suunnittelussa se on usein, koska eksponentiaalinen funktio y = e^x Se on läsnä esimerkiksi mekaniikassa ja sähkömagneettissa. Monien sovellusten joukossa voimme lainata:

-Kaapeli tai ketju, joka ripustaa päähän, ottaa käyttöön antaman käyrän muodon:

y = (e^x + ja^-x) /2

-Lauhdutin C purkautui alun perin, joka yhdistää sarjassa vastus r ja jännitteen lähteen V lataamaan, hankkii tietyn kuormituksen q riippuen siitä, mitä annetaan:

Q (t) = CV (1-E^-T/RC-A

biologia

Eksponentiaalinen funktio y = a.ja^Bx, A- ja B -vakiona sitä käytetään solujen kasvun ja bakteerien kasvun mallintamiseen.

Fyysinen

Ydinfysiikassa radioaktiivinen rappeutuminen ja ikäryhmien määrittäminen on mallinnettu päivätty radiohiili.

Talous

Yhdistelmäkoron laskennassa luku E syntyy luonnollisesti.

Oletetaan, että sinulla on tietty määrä rahaa P_jompikumpi, sijoittaa se vuotuiseen korkoon.

Jos rahat jätetään vuodeksi, sen jälkeen sinulla on:

P (1 vuosi) = P_jompikumpi + P_jompikumpi.I = P_jompikumpi (1+ i)

Toisen vuoden kuluttua koskettamatta sitä, sinulla on:

Voi palvella sinua: teoreettinen todennäköisyys: Kuinka saada se ulos, esimerkkejä, harjoituksia

P (2 vuotta) = P_jompikumpi + P_jompikumpi.I + (P_jompikumpi + P_jompikumpi .i) i = P_jompikumpi +2 p_jompikumpi.I + P_jompikumpi.Yllyttää²  = PO (1+i)²

Ja tällä tavalla n vuotta:

P = p_jompikumpi (1+i)ⁿ

Muista nyt yksi E: n:

Se näyttää vähän kuin P: n ilmaisu, joten suhde on oltava.

Jaamme nimelliskoron Yllyttää sisään n Aikajaksot, tällä tavalla yhdistelmäkorko on I/N:

P = p_jompikumpi [1+ (I/N)]ⁿ

Tämä ilmaisu näyttää hiukan enemmän rajamme, mutta se ei ole vielä täsmälleen sama.

Joidenkin algebrallisten manipulaatioiden jälkeen voidaan kuitenkin osoittaa, että tämän muuttujan muutoksen tekeminen:

h = n/i → i = n/h

Rahamme p tulee:

P = p_jompikumpi [1+ (1/h)]^Hei = P_jompikumpi [1+ (1/h)]^hYllyttää

Ja mikä on avaimien joukossa, vaikka se olisi kirjoitettu kirjaimella h, Se on yhtä suuri kuin rajan argumentti, joka määrittelee lukumäärän E, puuttuen vain rajan ottaminen.

Tehdään  h → ∞, ja mikä näppäinten välillä on muutettu numeroksi ja. Tämä ei tarkoita, että meidän on odotettava äärettömän suurta aikaa rahan nostamiseksi.

Jos näytämme hyvältä, kun teet H = n/i Ja ∞ ∞: lle, mitä olemme todella tehneet, on jakaa korko hyvin, hyvin pieninä ajanjaksoina: hyvin pieni:

I = n/h

Tätä kutsutaan Jatkuva isku. Tässä tapauksessa rahan määrä lasketaan helposti seuraavasti:

P = p_jompikumpi .ja^Yllyttää

Missä olen vuotuinen korko. Esimerkiksi tallettamalla 12–9 % vuodessa jatkuvan pääoman kautta, yhden vuoden kuluttua sinulla on:

P = 12 x e^{0 -.09 × 1} € = 13.13 €

Voitolla 1.13 €.

Viitteet

1. Nauti matematiikasta. Yhdistelmäkorko: jaksollinen koostumus. Toipunut.com.
2. Figuera, J. 2000. 1. matematiikka. Monipuolinen. Co-bo-painikkeet.
3. Garcia, m. Alkuperäisen laskelman numero E. Toipunut: matematiikka.Kisat.UCV.mennä.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Larson, r. 2010. Muuttujan laskenta. 9NA. Painos. McGraw Hill.