Parittomat luvut

Mitkä ovat parittomat numerot?

Se parittomat luvut Ne ovat kokonaisia ​​lukuja, jotka eivät ole jaettavissa 2: lla. Tämä tarkoittaa, että parittomilla määrillä et voi tehdä 2: n ryhmiä, esimerkiksi jos jollakin on 9 karkkia jaettavaksi ystävän kanssa etkä halua jakaa mitään, he koskettavat 4 karkkia ja muuta 5.

Jotkut parittomista numeroista ovat seuraavat: ... -5, -3, -1, 1, 3, 5, 7, 9, 11, 13 ..  Tässä lausekkeessa keskeiset kohdat osoittavat, että lukuja on enemmän, sekä vasen että oikea.

Kuva 1: Kuinka tietää, onko numero pariton?

Tarkasteltaessa voit nähdä, että jokainen pariton numero voidaan saada lisäämällä 2 edelliseen numeroon. Esimerkiksi, jos lisäämme 2 --1, saat 1, jos teemme 1 + 2, se on 3 ja niin edelleen.

Havaitaan myös, että jos parit ovat välissä, mukaan lukien 0, jota pidetään parillisena numerona, kokonaislukujoukko saadaan Z -z.

Siksi mikä tahansa pariton luonnollinen lukumäärä voidaan kirjoittaa muodossa 2n + 1, missä n = 0, ± 1, ± 2, ± 3, ± 4, ± 5…, missä symboli ± tarkoittaa, että sitä voidaan pitää positiivisena tai negatiivisesti.

Suurempien lukujen tapauksessa se voidaan tunnistaa, kun se on pariton, koska se loppuu aina 1, 3, 5, 7 tai 9. Esimerkiksi 1571 on pariton ja samoin negatiivinen kokonaisluku -152.489.

Esimerkkejä parittomista numeroista

Parittomat luvut esitetään usein luonteeltaan, ja heidän joukossaan numero 3 on erityinen merkitys. Katsotaanpa joitain esimerkkejä:

-On monia kukkia, joissa on pariton määrä terälehtiä.

-Meillä on 5 sormea ​​kummassakin kädessä.

Voi palvella sinua: satunnaismuuttuja: käsite, tyypit, esimerkit

-Ihmisillä on 23 kromosomia paria.

-Newtonin 3 laki ja 3 termodynamiikan laki.

-Niiden atomien ytimet, joilla on pariton määrä protoneita ja neutroneja, ovat vähemmän stabiileja kuin ne, joilla on pari.

-Magit ovat 3.

-Tarinoissa ja tarinoissa numero 3 ilmestyy usein, esimerkiksi romaanit, kuten Kolme muskettisoturia kirjoittanut alejandro dumas ja suosituissa tarinoissa, kuten Kolme veljeä ja Kolme pientä porsasta.

-Taiteelliselle sävellykselle on puhelu Outo sääntö, joka osoittaa, että koostumus, jolla on pariton määrä elementtejä, on houkuttelevampi kuin parin kanssa. Pariton luku lisää dynaamisuutta, kun taas yksi pari tarjoaa vakauden.

Kuva 2. Pariton määrä elementtejä lisää dynaamisuutta kuvaan

-Yleinen strategia esineiden hintojen näyttämiseksi halvemmiksi on lopulta 9, esimerkiksi 2.99 dollaria, 39 dollaria ja niin edelleen.

-Jotkut pitävät numeroa 13 huonoa onnea, kun taas toiset omistavat mystiset ominaisuudet 11: een, molemmat parittomat luvut.

Primo -numerot

Primo -numerot, ne, jotka vain myöntävät jakautuneiksi ja 1, ovat outoja, lukuun ottamatta 2, mikä on ainoa serkkunumero vääntömomentti.

On mahdollista osoittaa, että mikä tahansa luku voidaan jakaa ensisijaisten tekijöiden (mukaan lukien nämä voimat) tuotteena ja että tämä lukumäärä on ainutlaatuinen, paitsi tekijöiden järjestyksessä.

Esimerkiksi numero 45 voidaan hajottaa AS 45 = 3³ x 5.

Pariton luku

Odd -lukujen kanssa kaikki aritmeettiset toiminnot suoritetaan, ja joillakin on erinomaiset ominaisuudet.

Voi palvella sinua: Ilmaisujen symbolointi

- Summat ja tuotteet

-Kahden parittoman luvun summa johtaa parilliseen lukumäärään: 3+5 = 8; 11+15 = 26; (-10)+ (+6) = - 4.

-Lisäämällä parittoman luvun yhdellä vääntömomentilla, tulos on pariton: 7+2 = 9; 26+ 9 = 35; (-5) + 12 = 7.

-Jos n Ensimmäinen luonnollinen, pariton ja peräkkäinen lukumäärä tulos on n². Katsotaanpa tämä hieman yksityiskohtaisemmin:

N = 2: lle: 1 + 3 = 4 = 2²

N = 3: lle: 1 + 3 + 5 = 9 = 3²

N = 4: 1 + 3 + 5 + 7 = 16 = 4²

-Kun pariton kerrotaan parilla, parillinen luku on peräisin: 7 x 4 = 28; (-3) x 12 = -36.

-Kahden parittoman lukumäärän kertominen saadaan myös parittomi: 3 x 5 = 15; (-5) x (+11) = -55.

- Valtuudet

-Kun positiivinen luku nostetaan parittomaan voimaan, se on positiivinen luku, esimerkiksi: 3³ = 27.

-Nostamalla negatiivinen luku parittomaksi voimaan, tulos on negatiivinen: (-2)³= (-2) x (-2) x (-2) = -8.

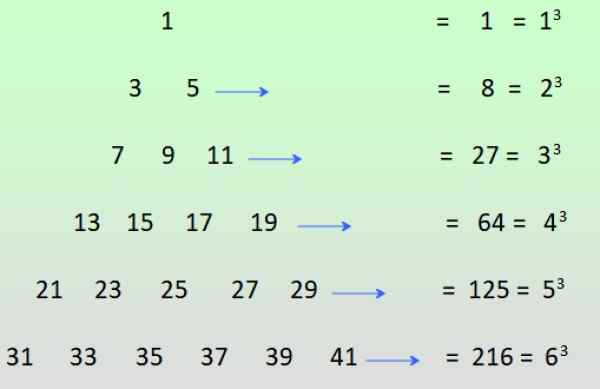
-Positiivisten kokonaislukujen parittomat voimat voidaan saavuttaa, jos kuviossa on saatavana parittomia lukuja ja rivit lisätään:

Kuva 3. Parittomien voimien hankkiminen parittomien lukujen summasta. Lähde: f. Zapata.

Ratkaisut

- Harjoitus 1

Päätä, onko seuraavan operaation tulos tasaisesti vai outo:

(53476890083 + 1987628967) x 13567903

Ratkaisu

Saadaksesi vastauksen sinun ei tarvitse ajaa etsimään laskin. Katsotaanpa lisäysten viimeisiä numeroita, jotka ovat vastaavasti 3 ja 7:

53476890083  + 1987628967

Tämä tarkoittaa, että addiktit ovat outoja ja tiedämme jo, että kahden parittoman numeron summa on jopa.

Siksi suluista johtuva luku on tasainen ja kerrotaan numerolla, joka loppuu 3:

Voi palvella sinua: Vector Algebra

13567903

Mikä tarkoittaa, että tämä luku on outoa.

Edellä kuvattujen ominaisuuksien mukaan todettiin, että vääntömomentin X kertominen on parillinen luku. Siksi tuloksena oleva toimenpide on jopa.

- Harjoitus 2

Kuinka paljon ensimmäisen viiden peräkkäisen parittoman numeron summa on? Ja ensimmäisten 50?

Ratkaisu

Ensimmäisen viiden peräkkäisen parittoman numeron summa on:

1 + 3 + 5 + 7 + 9 = 25

Mutta jos haluamme lisätä ensimmäiset 50 tällä tavalla, se on hankala, niin olemme menossa ominaisuuksiin. He väittävät, että peräkkäisten parittomien lukujen summa on n². Tässä tapauksessa n = 50 ja pyydetty summa on:

viisikymmentä² = 50 x 50 = 2500.

- Harjoitus 3

Kun lisätään kolme peräkkäistä parittomia lukuja, saadaan 237. Mitkä ovat numerot?

Ratkaisu

Soitakaamme ensimmäiseen parittomaan numeroon ja toinen ja z kolmanteen, lausunnon mukaan on täytettävä, että:

x + y + z = 237

Algebrallisella kielellä mikä tahansa pariton luku voidaan kirjoittaa muodossa 2n +1. Tehdään ensimmäinen pariton numero:

x = 2n +1

Lisätään 2 saadaksesi seuraavan pariton:

y = x + 2 = (2n + 1) + 2 = 2n + 3

Ja lopuksi se lisätään uudelleen 2 kolmannen parittoman saamiseksi:

Z = (2n +3) + 2 = 2n + 5

Kaikki tämä lisää:

2n + 1 + 2n + 3 + 2n + 5 = 237

6N + 9 = 237

Tämä johtaa yksinkertaiseen lineaariseen yhtälöön, jonka ratkaisu on:

n = 38

Ja nyt arvolla n = 38 on kolme tilausta:

x = (2 × 38) + 1 = 77

Seuraavat ovat outoja peräkkäisiä, siksi:

y = 79

Z = 81

Ja lukija voi helposti varmistaa, että kolmen summa on 237.

Viitteet

1. Baldor, a. 1986. Aritmeettinen. Codex -versiot ja jakaumat.
2. Lähiöt, L. Parittomat numerot ja luonnollisten lukujen voimat. Haettu: Sinewton.org.
3. Loistava. Pariton luku. Toipunut: loistava.org.
4. Matematiikka 18. Pariton luku. Haettu: Matematiikka18.com.
5. Wikipedia. Pariton luku. Palautettu: on.Wikipedia.org.